st表

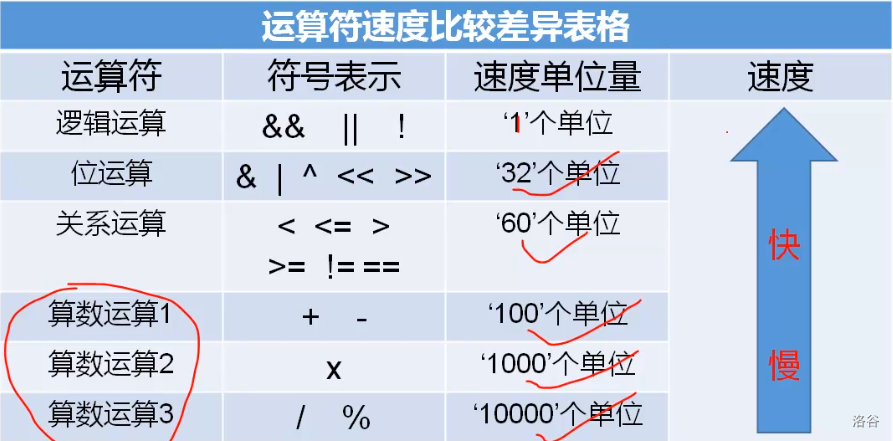
位运算

与& 或| 异或^ 左移<< 右移>>

\(x<<y=x·2^{y}\)

\(x>>y=\frac{x}{2^{y}}\)

\(2a+1=(a<<1)|1\)

\(a\)%\(2=a\)&\(1\)

st表

当st表合并的复杂度为\(O(1)\)时，st表构建的复杂度为\(O(nlogn)\),查询的复杂度为\(O(1)\)，但是st表并不支持修改。

求区间最大值/最小值：复杂度\(O(n)\)

st表的核心在于倍增和DP。

\(f[i][j]\)表示以第\(i\)个数作为左端点，长度为\(2^{j}\)的区间的最值，也就是\([i,i+2^{j}-1]\)的区间最值。

\(f[i][0]=a[i]\)

\(f[i][j]=merge(f[i][j-1],f[i+2^{j-1}][j-1])\)

询问一个区间\([l,r]\)的区间最值，

区间的极值就是两个长度为\(2^{k}\)的子区间的极值。

设 $ k = \left \lfloor log ( r - l + 1 ) \right \rfloor $ ,那么，

\(ans=merge\{f[l][k],f[r-2^{k}+1][k]\}\)

merge函数表示信息合并，询问最大值时用max，询问最小值时用min。

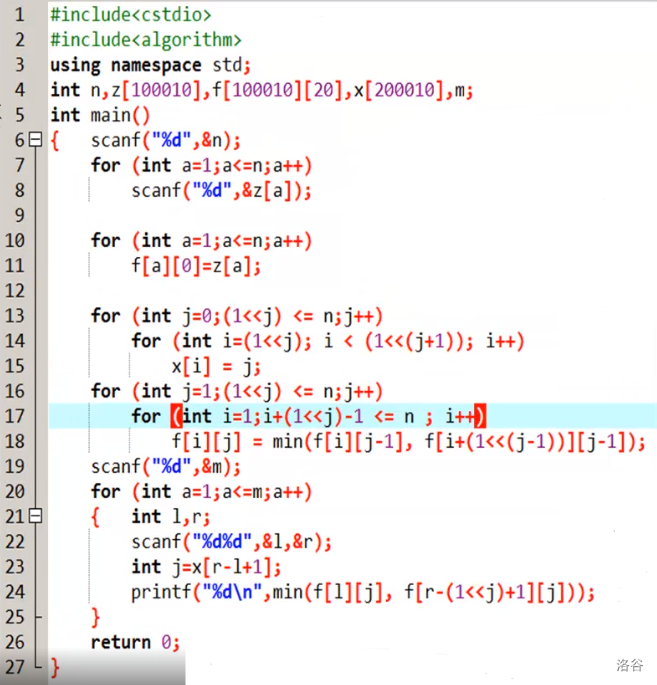
例题

【问题描述】

我们有一个n行m列的矩阵。

K次询问矩阵矩阵最值。

注意

1、如果块重叠对最后的答案有影响，那么不能使用st表处理。

2、调用一次cmath库中的\(log_{2}\)函数时间复杂度是\(O(logn)\)的，我们可以预处理出Log数组。

并非原创，仅是整理，请见谅