Minimum dot product query

Minimum dot product query (最小点积查询) : 若有一个二维向量集合V, 其大小为m. 那么在集合V上的一次最小点积查询即是说任意输入一个向量x, 返回在V中与x的点积最小的元素以及相应的点积，即 min{dot(x, vi) | vi 属于 V}。

这个问题是在cstheory.stackexchange上面看到的。楼主提出的问题原本是n维的最小点积查询，然后顺便提了下如果n=2, 则“immediate”就能得到一个(logm)^2的算法。我想了半天不知道他这个(logm)^2的复杂度是怎么弄出来的，但是事际上若n=2, 其实马上可以得到一个logm的算法。

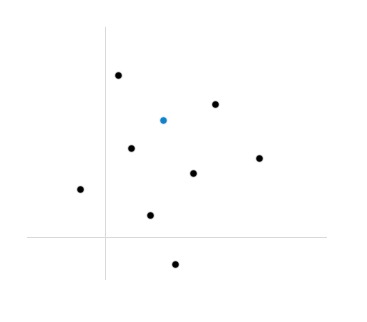
首先一个观察是x的长度并不影响最后的结果（忽略那个||x||倍的缩放），所以可以假设x均为单位向量， 于是任意dot(vi, x)即是vi在x方向上的投影。这就给了我们一个启发：最小点积只能在V的凸包顶点处获得。

图1： V（黑色）与x(蓝色)

于是可以先求得V的凸包， 然后就将问题转化到求一个凸包投影到某个方向上后的端点。

图2: V 的凸包, 以及投影到x方向的最小点

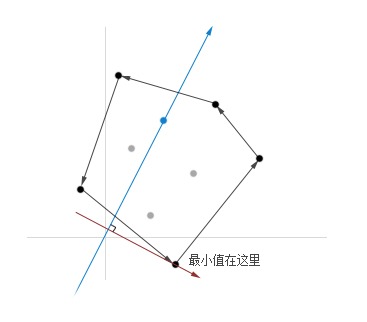
如果凸包的边向量依次形成一个序列E，那么求凸包投影到x方向上的最小点即相当于将x旋转90度后(见图2中红色箭头)插入到E中的合适位置上。这可以通过二分法来得到，只是需要定义一个合适的序。这个序可以用叉乘来定义，但是为了避免形成一个环，即出现a < b < c < d < a的情况, 一个方法是将向上的向量与向下的向量分开，如下所示：

bool less(const double2 &lhs, const double2 &rhs)
{
	if (lhs.y >= 0 && rhs.y < 0) return true;
	if (lhs.y == 0 && rhs.y == 0 && lhs.x > 0 && rhs.x < 0) return true;
	return cross(lhs, rhs) > 0;
}

序定义好了之后，直接std::lower_bound一下即可。整个算法的预处理时间为O(mlogm), 查询为O(logm), 这里还需要提一下的是空间复杂度，因为我们只需要存一个凸包即可，而随机分布在一个圆盘上的m个点其凸包的期望边数为O(m^(1/3)). 因此期望的空间复杂度为O(m^(1/3)).