HDU - Tree and Permutation

题目链接：https://acm.dingbacode.com/showproblem.php?pid=6446

思路：给你n以及n-1对连边与边权，要求出：n个点在每一种排列情况下 [ 从排列起始点走到终止点的边权和 ] 的和。

以下是对第2个测试数据的详细解释：

 

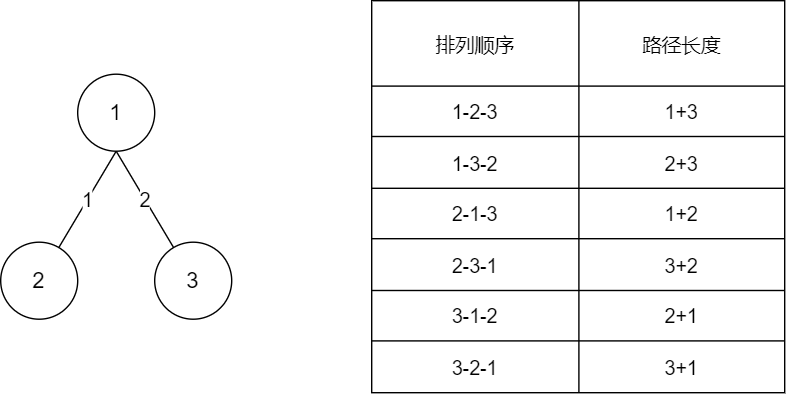
通过观察总结可以得出公式：$ans=sum*2*(n-1)!$

其中，sum​为图的任意两点边权和，所以接下来就是运用树上dp求sum​。

#include <iostream>
#include <algorithm>
#include <cstring>
#define ll long long
using namespace std;
const ll mod=1e9+7;
const int N=1e5+5,M=2*N;
int n,idx,e[M],ne[M],h[N];
ll w[M],sum,sz[N],inv[N];//sum记录树的边权和，sz记录子树大小，inv记录阶乘

void add(int a,int b,ll c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int x,int fa)
{
    sz[x]=1;
    for(int i=h[x];i!=-1;i=ne[i])
    {
        int y=e[i];
        if(y==fa) continue;
        dfs(y,x);
        sz[x]+=sz[y];
        sum=(sum+sz[y]*(n-sz[y])%mod*w[i]%mod)%mod;
    }
}

int main()
{
    inv[0]=inv[1]=1;
    for(int i=2;i<=N;i++)
    {
        inv[i]=(inv[i-1]*i)%mod;
    }

    while(~scanf("%d",&n))
    {
        memset(h,-1,sizeof h);
        memset(w,0,sizeof w);
        memset(sz,0,sizeof sz);
        idx=0,sum=0;

        for(int i=1;i<n;i++)
        {
            int x,y;
            ll z;
            scanf("%d%d%lld",&x,&y,&z);
            add(x,y,z),add(y,x,z);
        }

        dfs(1,-1);

        ll ans=((sum*2)%mod*inv[n-1])%mod;

        printf("%lld\n",ans);
    }

    return 0;
}

Bye~