牛客 - 删括号

题目链接：https://ac.nowcoder.com/acm/problem/21303

参考链接：https://ac.nowcoder.com/acm/problem/blogs/21303

思路：dp，动态规划的重点在于可以忽略中间步骤，适用于只是想知道方案数或者可行性的题目，因此可以对题目简化。输入字符串为a，目标字符串为b。删括号的时候一定要时刻保证左括号数量比右括号多或者等于（最后才等于），我们可以定义dpi[k]表示考虑a字符串前i个匹配了b字符串前j个，a字符串被删除部分左括号数-右括号数=k是否可行，分类讨论转移即可。

#include <bits/stdc++.h>
using namespace std;
const int N=105;
bool dp[N][N];//判断s的前i-1个是否存在方案与t中前j个位置匹配

int main()
{
    string s,t;
    cin>>s>>t;
    memset(dp,0,sizeof dp);
    dp[0][0]=1;//初始状态必然匹配
    
    for(int i=1;i<=s.length();i++)
    {
        for(int j=0;j<=t.length();j++)//注意这里j要从0开始
        {
            //相等就匹配
            if(s[i-1]==t[j-1]) dp[i][j]|=dp[i-1][j-1];
            //如果当前字符是)，找离这个括号最近的可以匹配的位置，那么就可以删除这个括号
            //如果删除这个括号后的括号是匹配的，那么当前状态匹配
            if(s[i-1]==')')
            {
                int loc=i-1;//最近的可以匹配的位置
                int cnt=1;
                
                while(cnt>0)//cnt=0的时候说明
                {
                    if(s[loc-1]==')') cnt++;
                    else cnt--;
                    loc--;
                }
                
                dp[i][j]|=dp[loc][j];
            }
        }
    }
    
    if(dp[s.length()][t.length()]) cout<<"Possible";
    else cout<<"Impossible";
    return 0;
}

还有一种思路，作为图论选手，做什么都能想到树，但当时没想出具体解法，在题解里正好看到有人也是用树做的，于是我学习了一手。

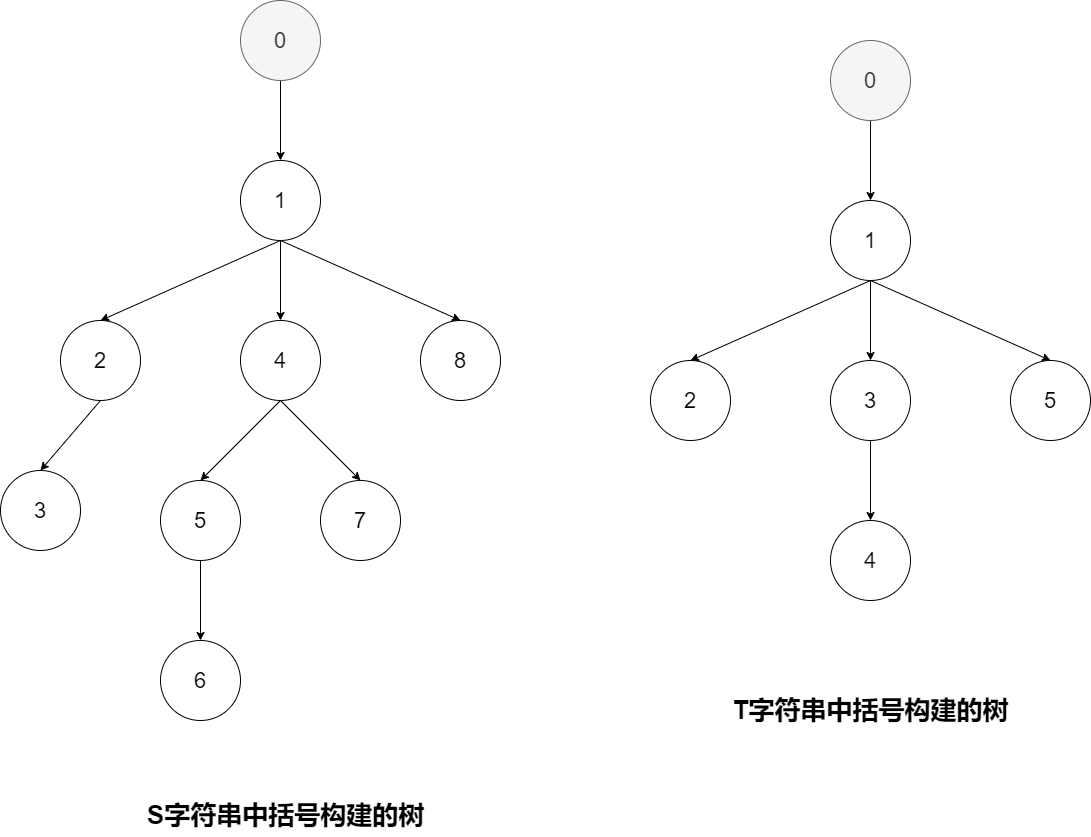
每一对括号看出一个节点，那么s和t字符串可以看成两棵树，只需要判断t是不是可以和s中某节点子树的部分重合即可。

这里以示例4为例，此时输入为

((())((())())())
(()(())())

S和T字符串对应的树如下：

 

 

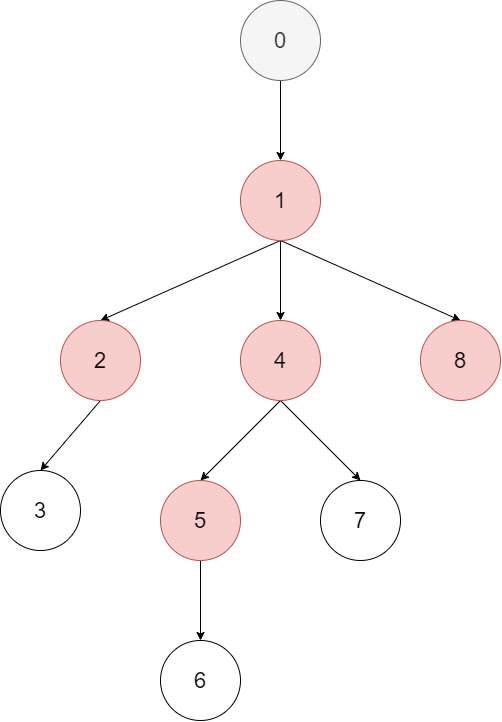
运用dfs进行深搜，找到S树中满足条件的覆盖（下图中的红色节点是T树在S树中的覆盖）。把代码中dfs函数的注释去掉，会发现输出的节点是S树和T树中对应的节点。

 

 

#include <bits/stdc++.h>
using namespace std;
const int N=105;
string s,t;
vector<int> ss[N],tt[N];
int fa[N];

//实际上判断一棵树能否嵌入另一棵树中就是是判断每个节点的子节点个数是否满足
bool dfs(int x,int y)
{
    //cout<<x<<" "<<y<<endl;
    int now=0;
    for(int i=0;i<tt[y].size();i++)
    {
        while(now<ss[x].size()&&!dfs(ss[x][now],tt[y][i])) now++;//往x与y节点的儿子节点深搜
        if(now==ss[x].size()) return false;
        now++;
    }
    return true;//如果能完全覆盖，那么返回true
}

int main()
{
    cin>>s>>t;
    
    int n=0,now=0;
    for(int i=0;i<s.length();i++)
    {
        if(s[i]=='(')
        {
            ss[now].push_back(++n);
            fa[n]=now;
            now=n;
        }
        else now=fa[now];
    }
    n=0,now=0;
    for(int i=0;i<t.length();i++)
    {
        if(t[i]=='(')
        {
            tt[now].push_back(++n);
            fa[n]=now;
            now=n;
        }
        else now=fa[now];
    }
    
    if(dfs(0,0)) cout<<"Possible";
    else cout<<"Impossible";
    
    return 0;
}

Bye~