洛谷 - 变换序列

题目链接：https://www.luogu.com.cn/problem/P1963

思路：匈牙利算法，由于需要输出字典序最小，所以要考虑匈牙利算法递归的顺序问题，从后向前递归时，前面的点如果需要修改就可以直接修改，所以这样的顺序会得到最小字典序。题中的距离公式可以通过转化，求得i对应的两个t[i]值。

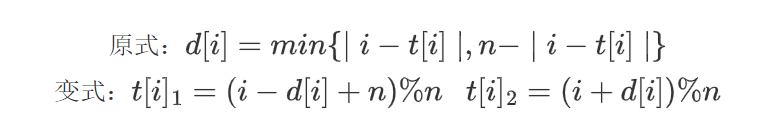
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int n,dis[N],ans;
int g[N][2],match[N],res[N];
bool vis[N];

bool dfs(int x)
{
    for(int i=0;i<2;i++)
    {
        int y=g[x][i];//可以匹配的就两个位置
        if(!vis[y])
        {
            vis[y]=true;
            if(match[y]==-1||dfs(match[y]))
            {
                match[y]=x;
                res[x]=y;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    cin>>n;
    memset(match,-1,sizeof match);
    for(int i=0;i<n;i++) cin>>dis[i];//不是t数组，而是距离

    for(int i=0;i<n;i++)
    {
        int minn=(i+dis[i])%n,maxx=(i-dis[i]+n)%n;
        if(minn>maxx) swap(minn,maxx);
        g[i][0]=minn,g[i][1]=maxx;
    }

    for(int i=n-1;i>=0;i--)
    {
        memset(vis,0,sizeof vis);
        if(dfs(i)) ans++;
    }

    if(ans<n) cout<<"No Answer";
    else
    {
        for(int i=0;i<n;i++)
        {
            cout<<res[i];
            if(i!=n-1) cout<<" ";
        }
    }

    return 0;
}

Bye~