计算机组成原理
计算机组成原理
第二章 计算机系统中的数据表示
一)数值数据的编码
1、补码
1)补码概念引入


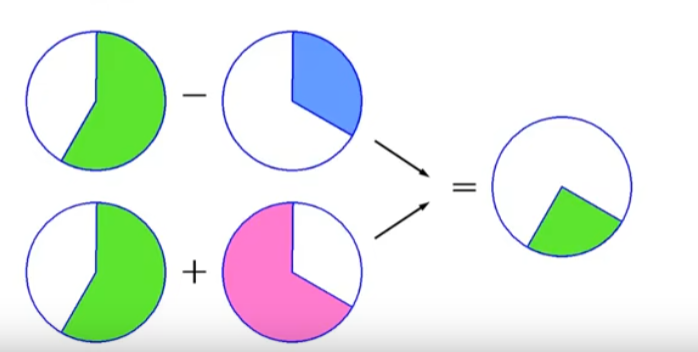
2)补码的定义

计算机中的浮点数是以纯小数和纯整数部分构成的,所以要表示一个浮点数只需要知道它的小数部分和整数部分怎么表示。
n位二进制纯小数的编码由一位整数位(也是符号位),和n-1位小数位组成,如1.1100111,0.0000111。其中整数位的0和1是符号位,0表示正数,1表示负数。对一个二进制数来说,它的模等于它的所有有效位都为1时给末位再加1,定点小数的模(以八位为例)1.1111001的模就为10.0000000也就是2。在这里的符号位也算作有效位。其实总结来说,对于n位二进制整数来说,它的模就等2^n。而二进制纯小数的模就是2。

补码相较于原码来说0是唯一的,所以补码可以表示2^n个数。

最小的负数的补码比较特殊,它的最高位既是符号位也是数值位。
3)补码的性质

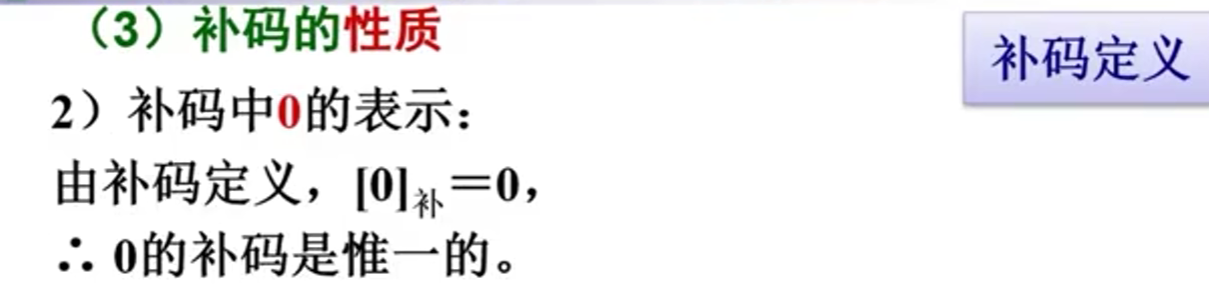

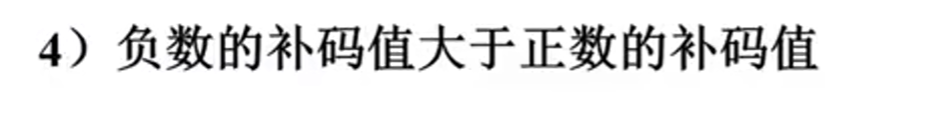
真值-->补码
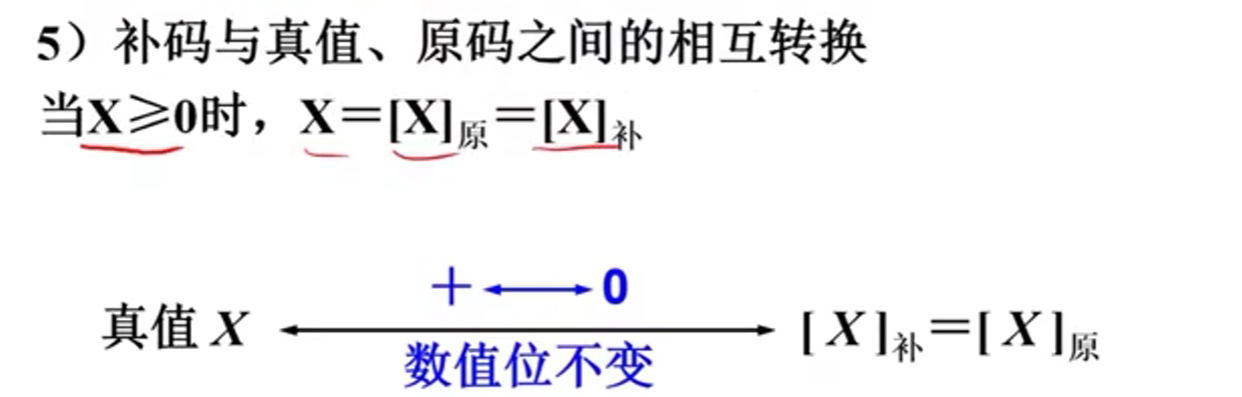
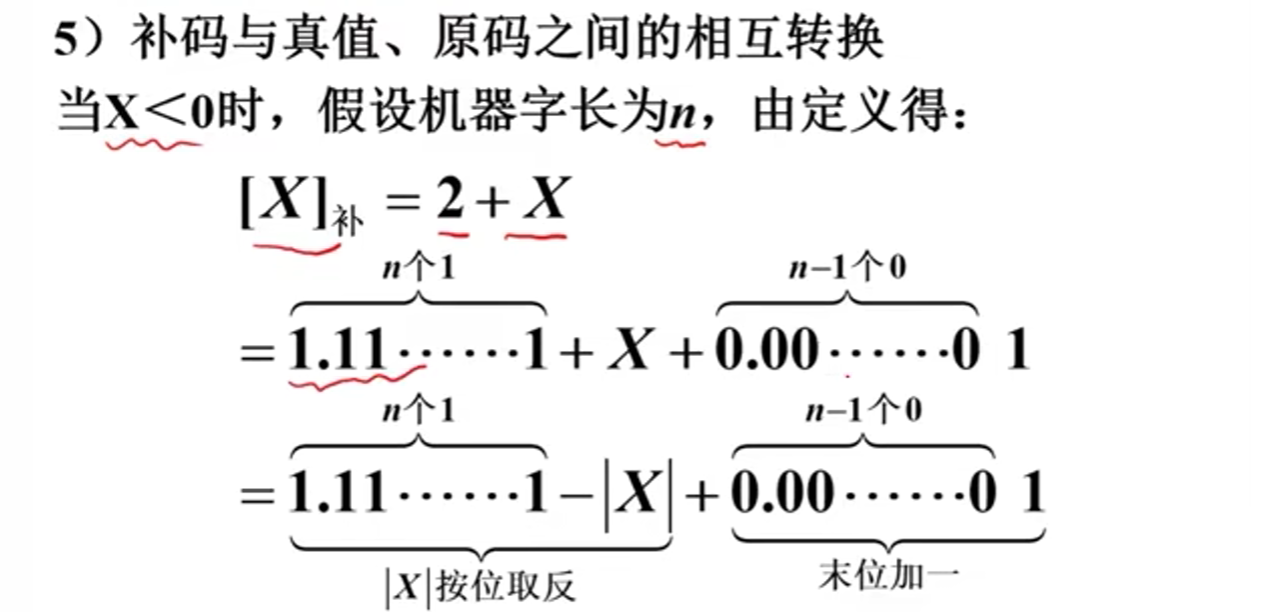
补码-->真值
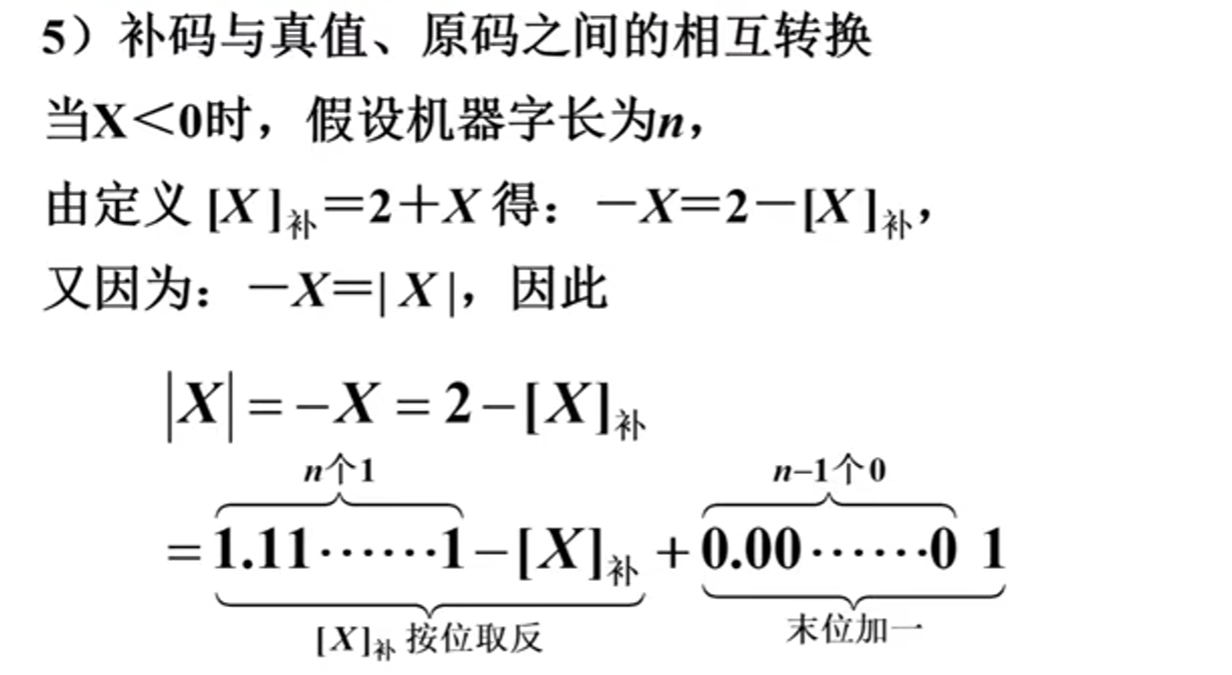
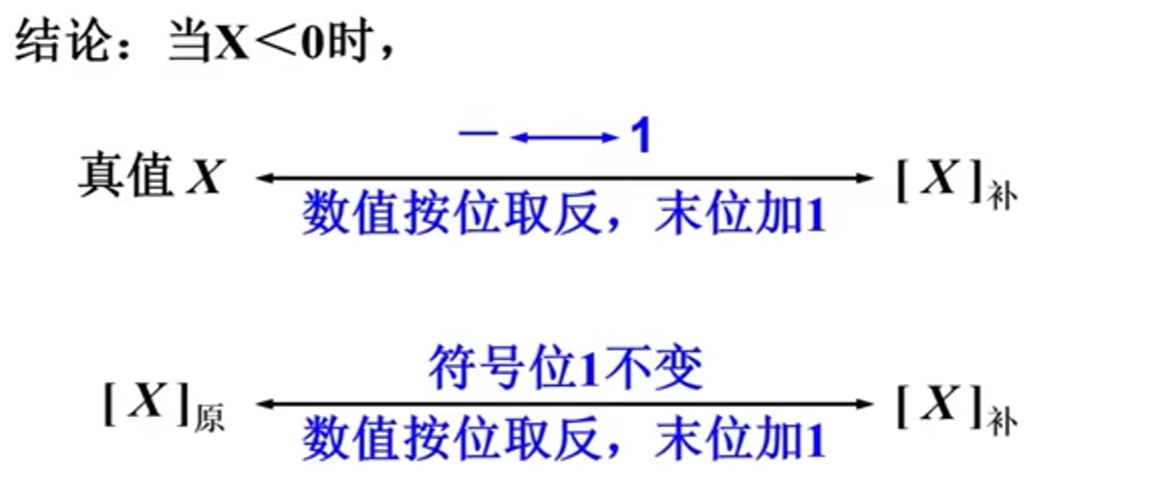
简化方法:







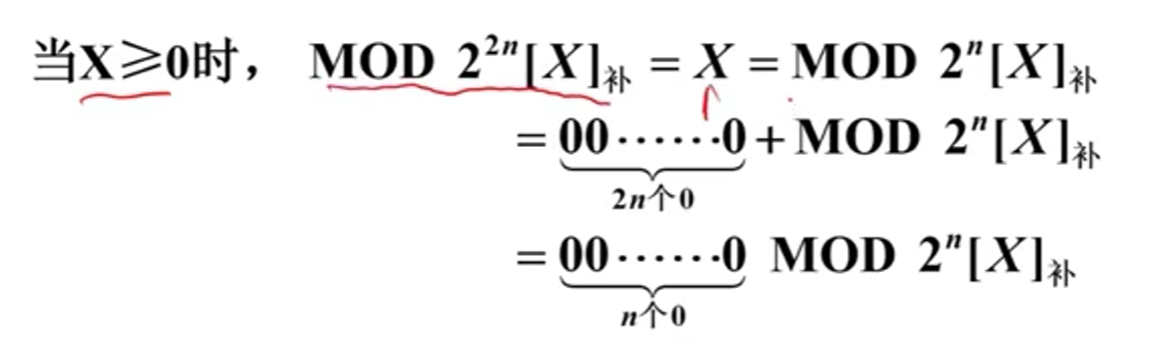
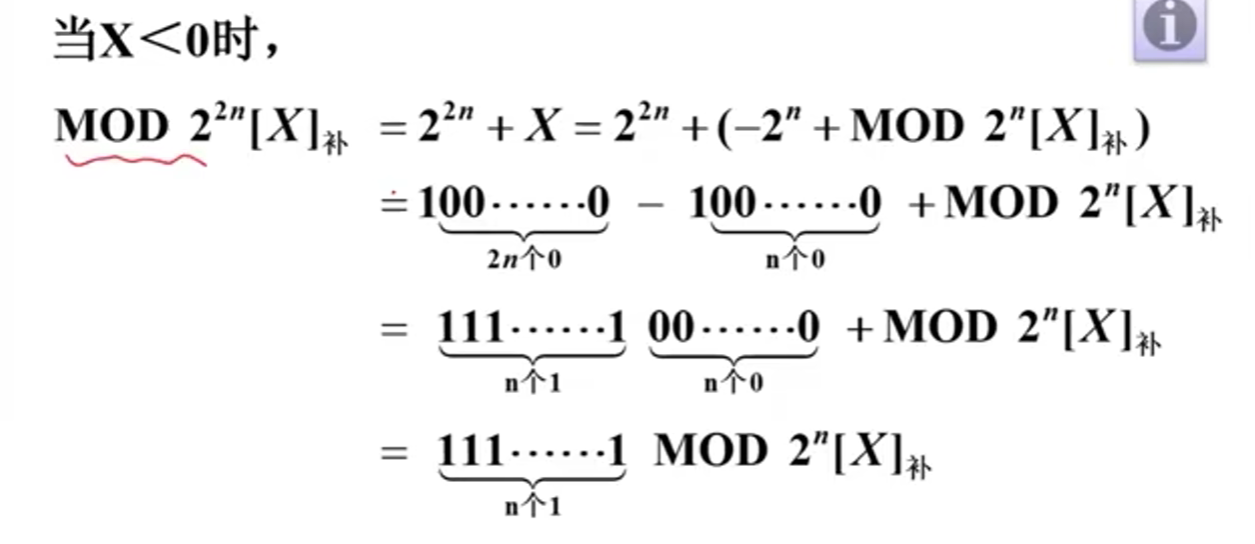




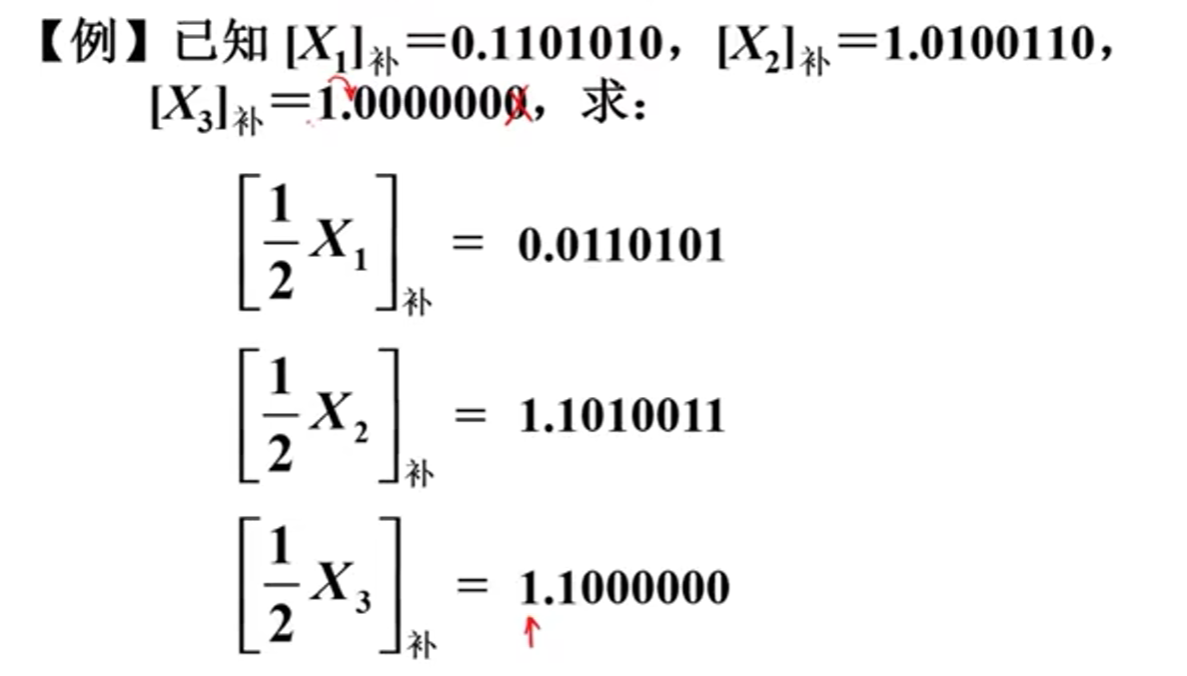


溢出说明已经超出了表示范围

2、反码(计算机中不使用)
1)反码的定义和表示
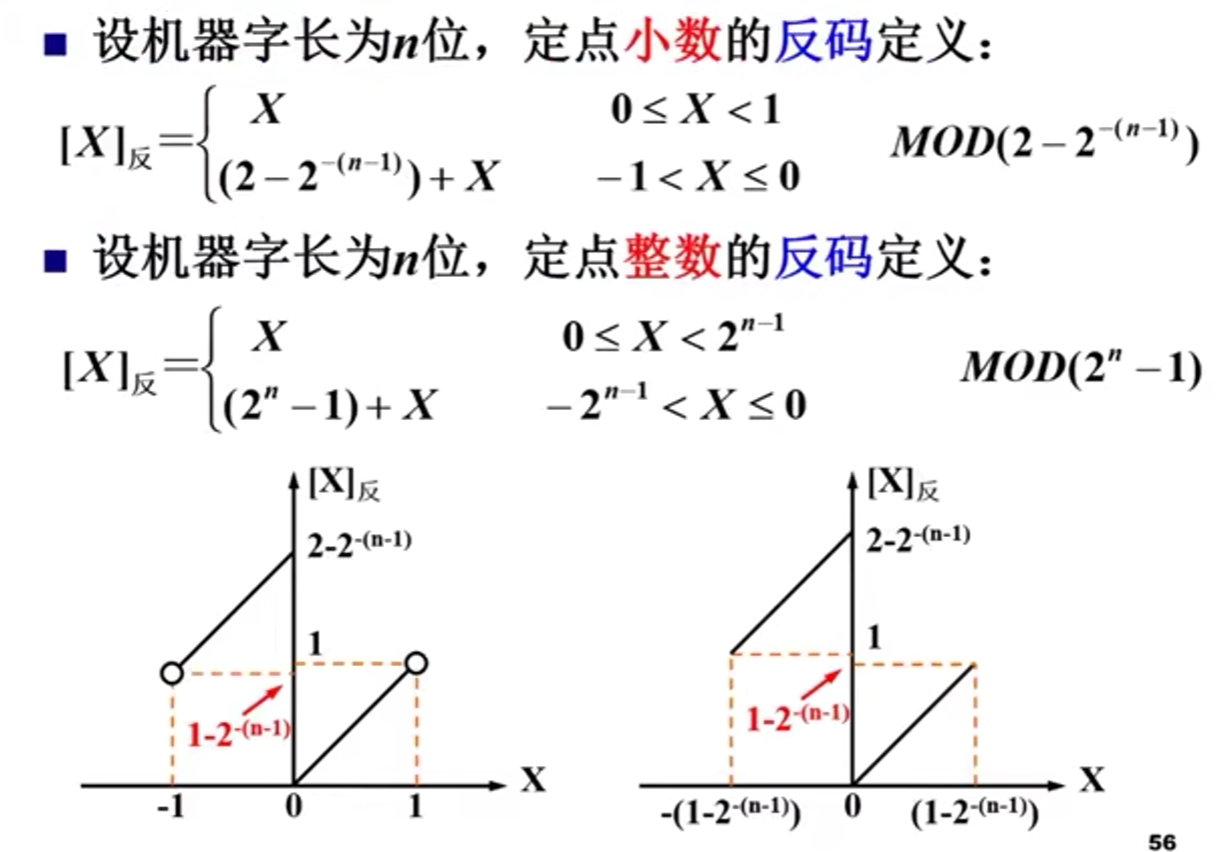
反码和补码的区别就是反码不需要末尾加一。
2)反码的性质![image-20230403203436965]()
3、移码
1)移码的引入
计算机中的浮点数的组成为:
当我们在比较两个浮点数时,在符号相同的情况下,我们先比较阶码的大小,当阶码一样时再去比较尾数,并且我们希望从阶码的高位向低位依次去进行比较。但是如果用原码或者补码来表示阶码,就会存在一个问题:负数的符号 位是1,正数的符号位是0,因此负数的符号位总是大于正数的符号位,这不利于我们从高位向低位依次的进行浮点数比较,而通过转换的方法又很麻烦,所以我们干脆设计一种新的编码,我们希望这种编码值和真值之间是线性正比的关系。
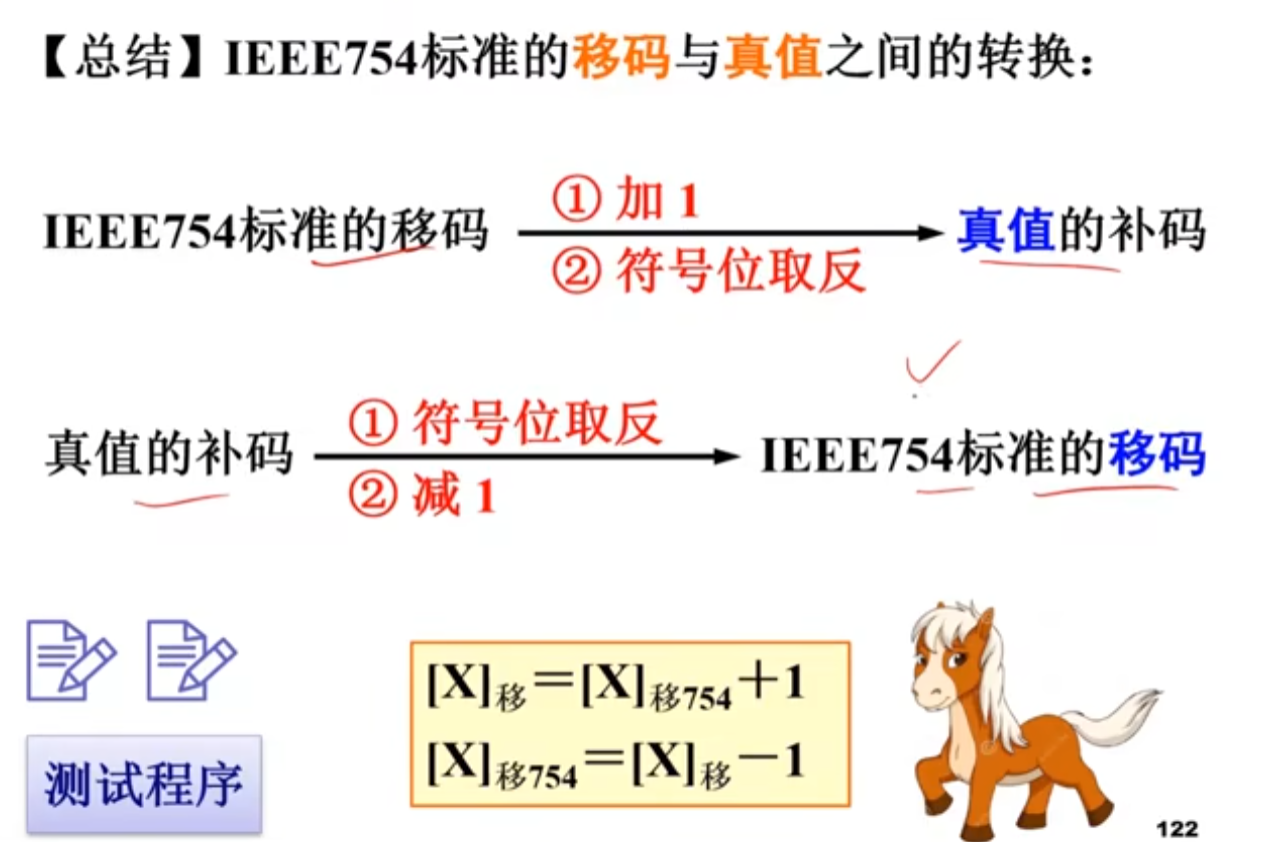
2)移码的表示

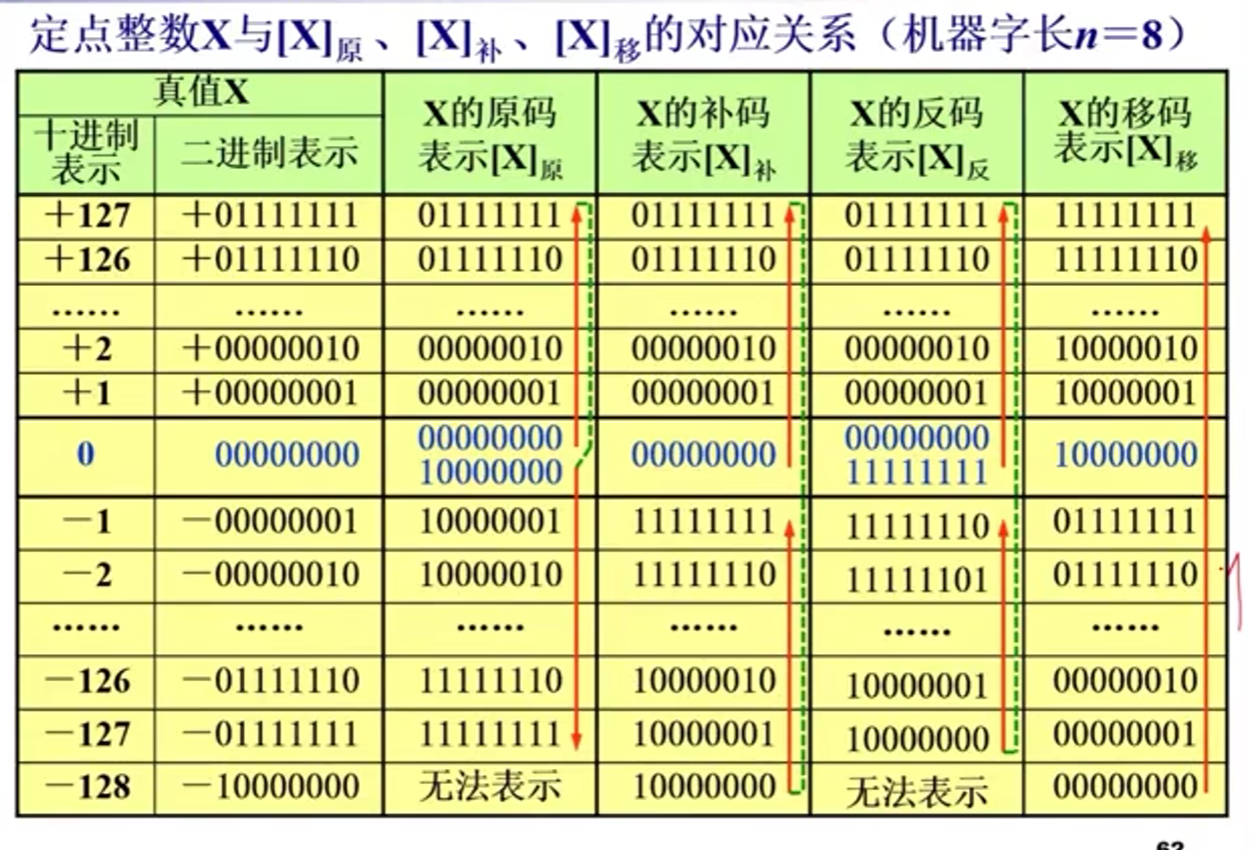
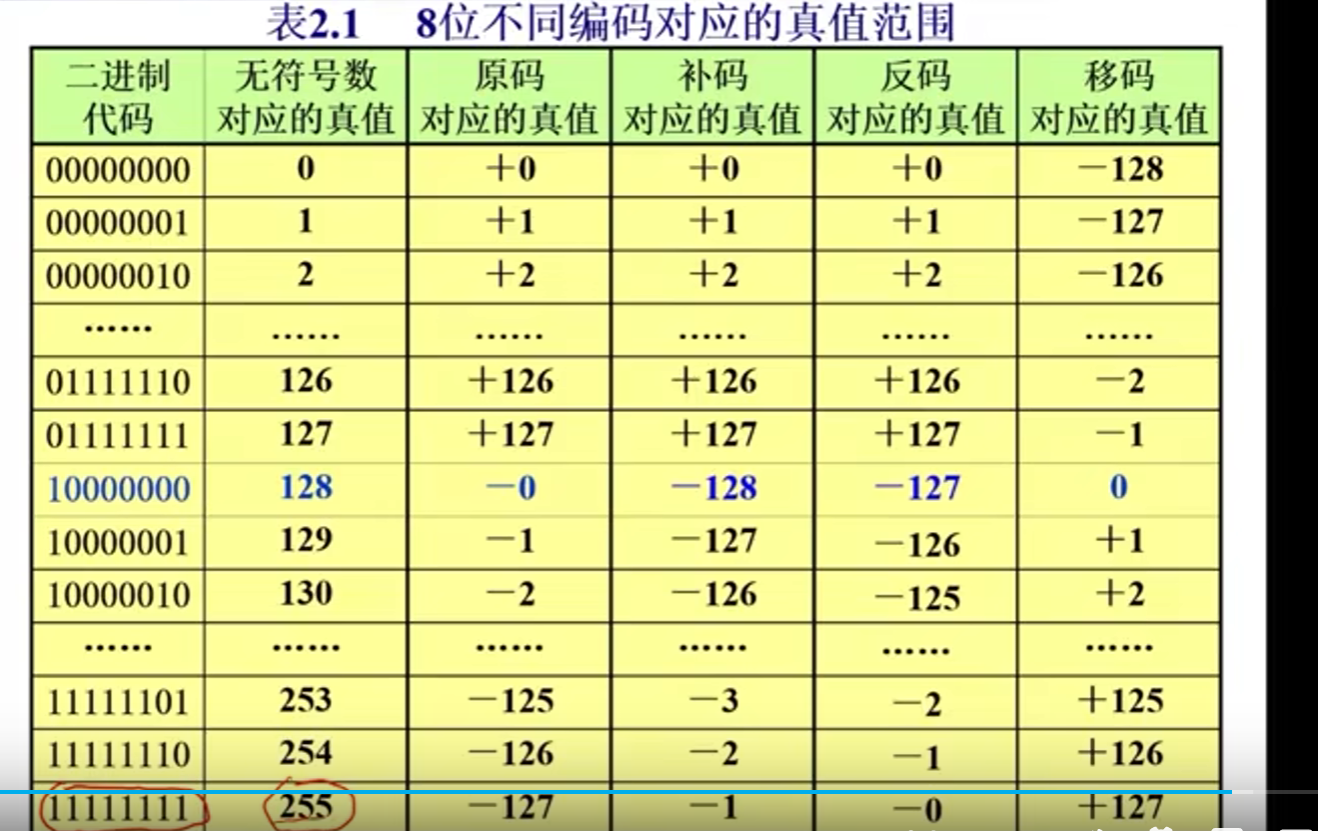
3)移码的性质
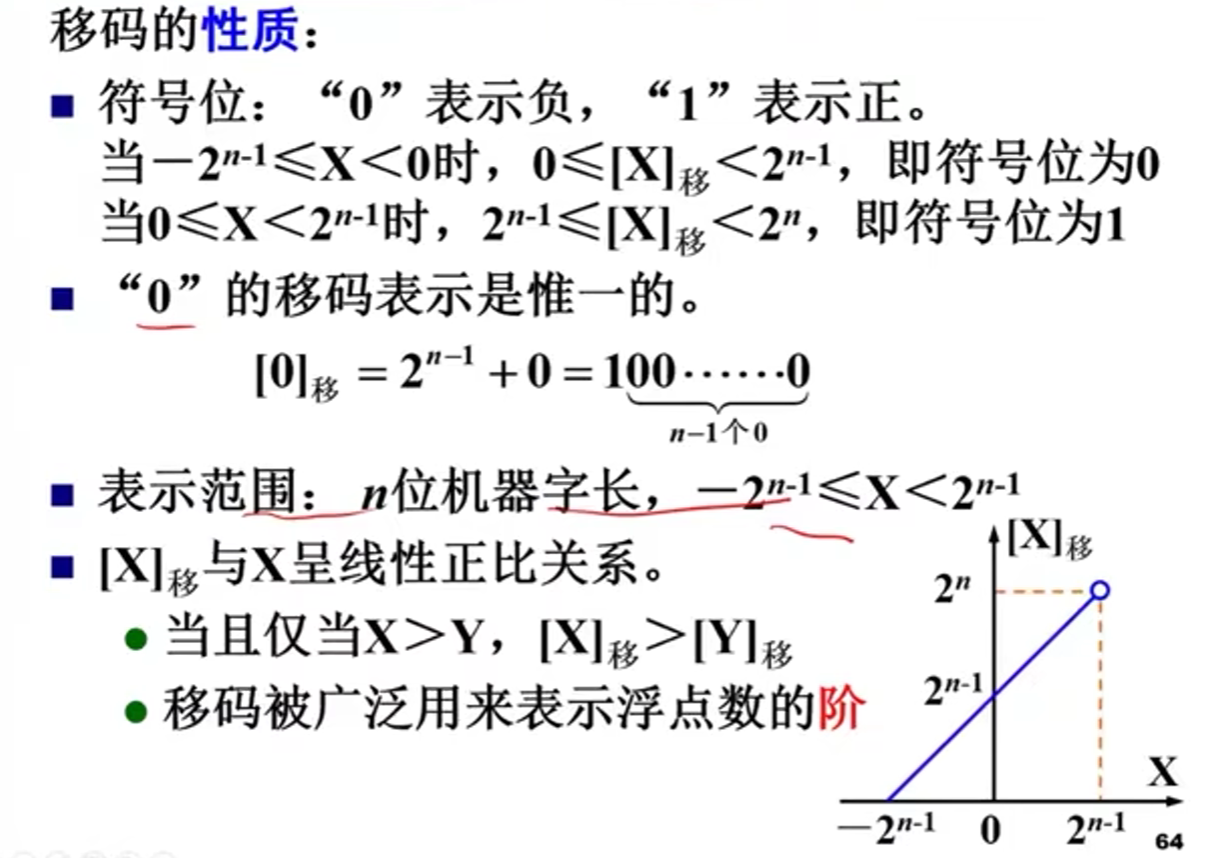
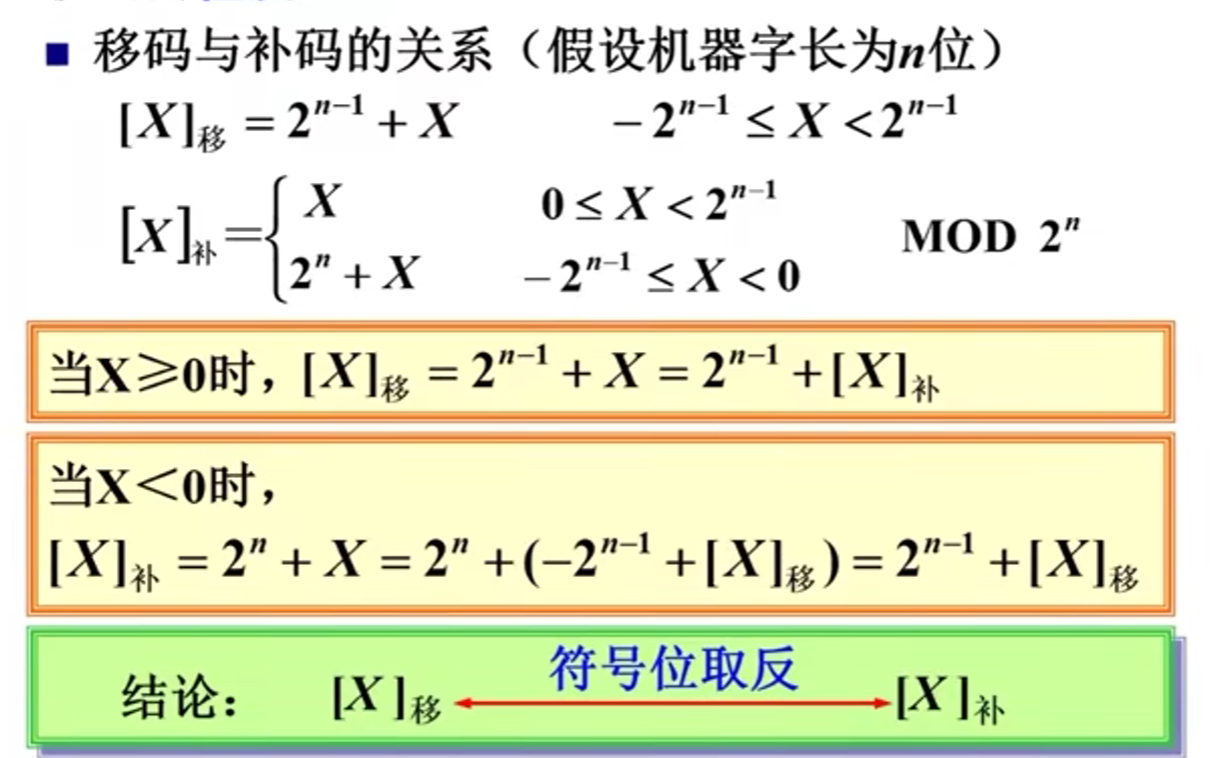
二)数据的浮点表示
1、浮点数在计算机中的表示

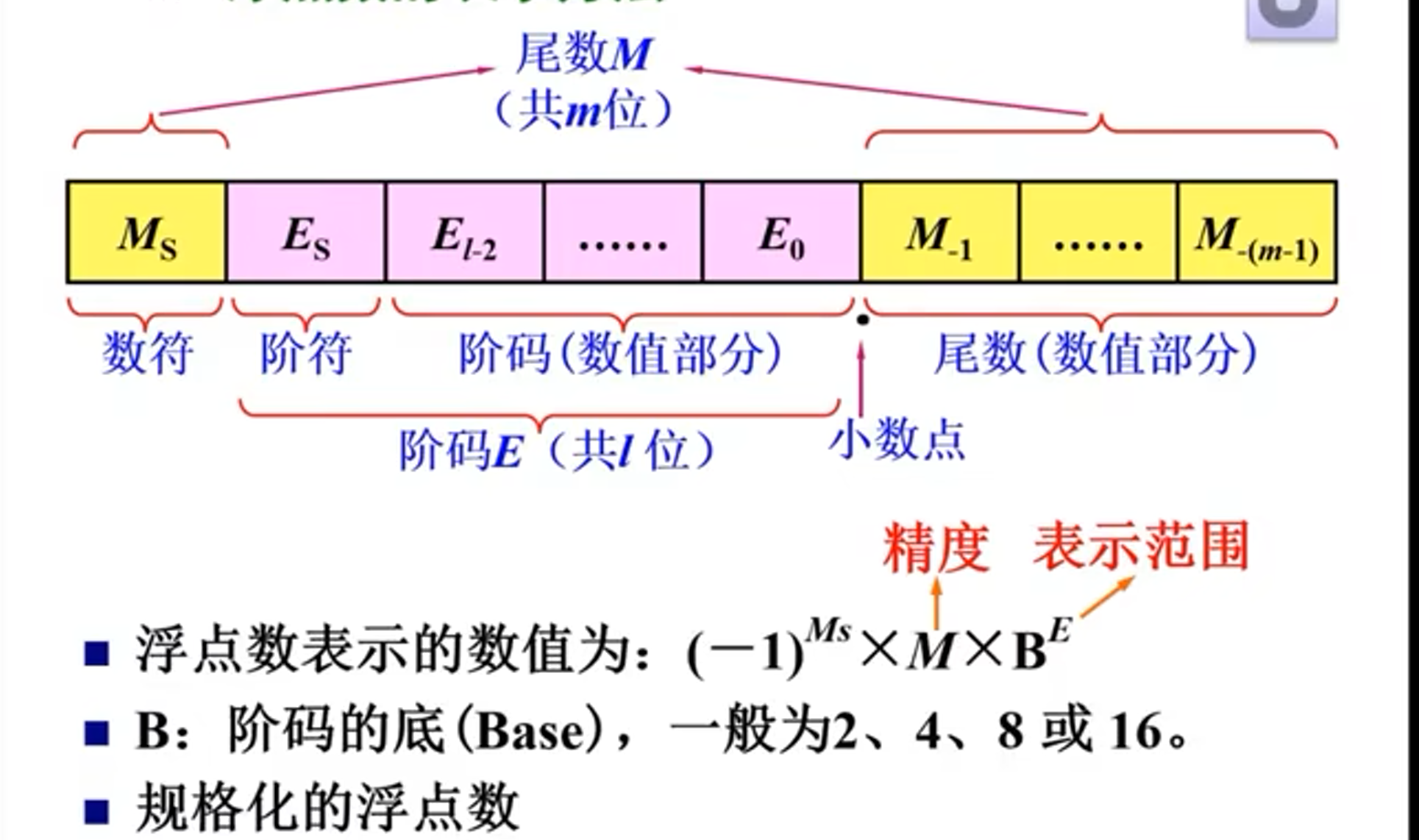
现在的计算机阶码的底默认都是2。
2、规格化的浮点数
计算机中采用的是二进制,因此尾数的表示也是二进制,类比于十进制的科学计数法,我们要对二进制进行一个规格化的处理。对于浮点数的尾数来说,它的第一位也就是整数位肯定必须要是0,而小数位的第一位要是1。原因就是如果一个尾数是0.0001110,那么小数部分的前三个0很明显会造成数值位的浪费,我们可以让他改进成0.11100000然后让它的阶码减3。总而言之,计算机中的浮点数需要被规格化,规格化之后需要满足原码为S.1XXXXXX(S为符号位),也就是小数位的第一位必须为1。
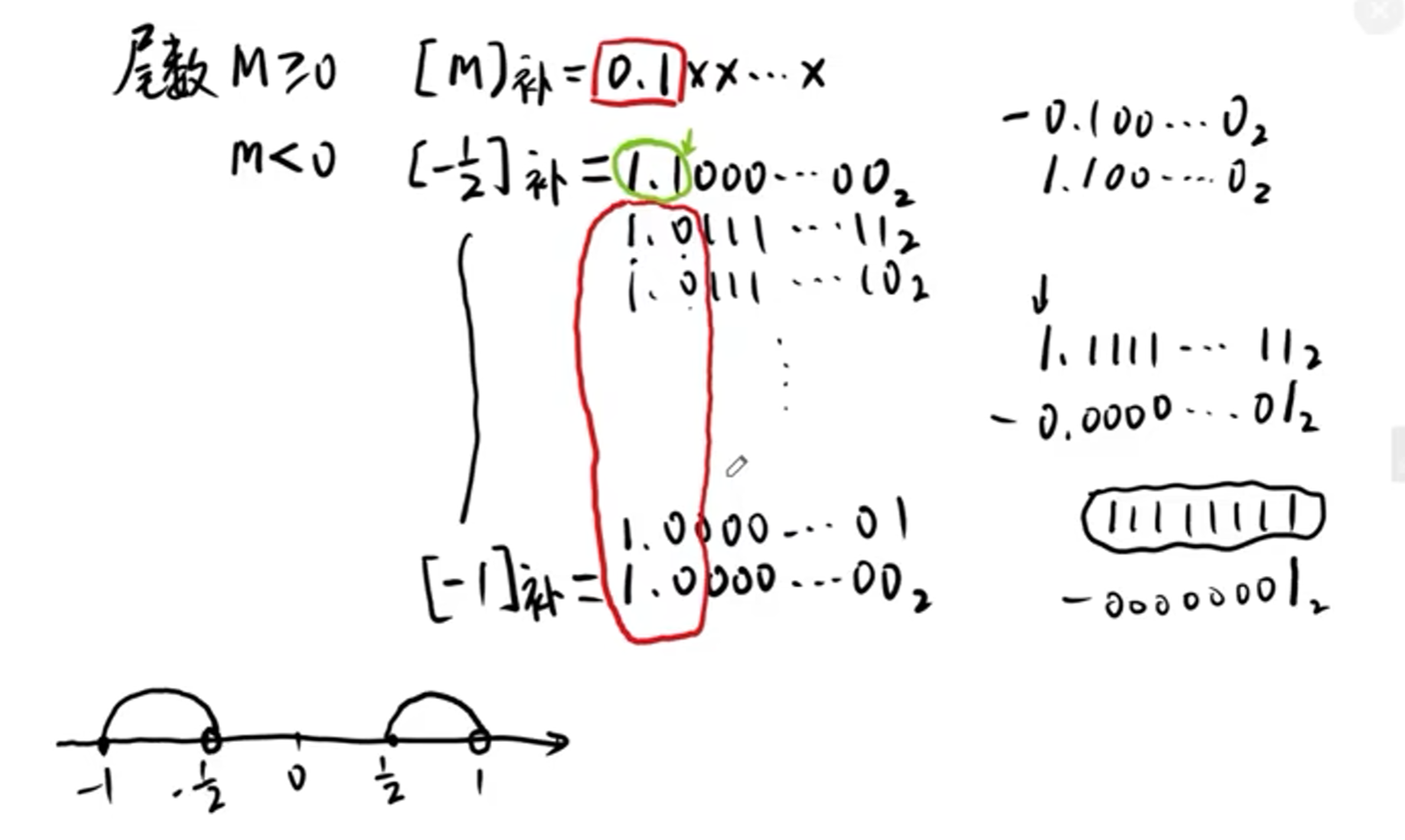

注:一般来说,计算机中浮点数的尾数使用原码表示,阶码使用移码表示。但是实际做题时题目可能会要求尾数用不同的编码表示,原码表示相对比较简单, 因此我们做出尾数用补码表示的情况。
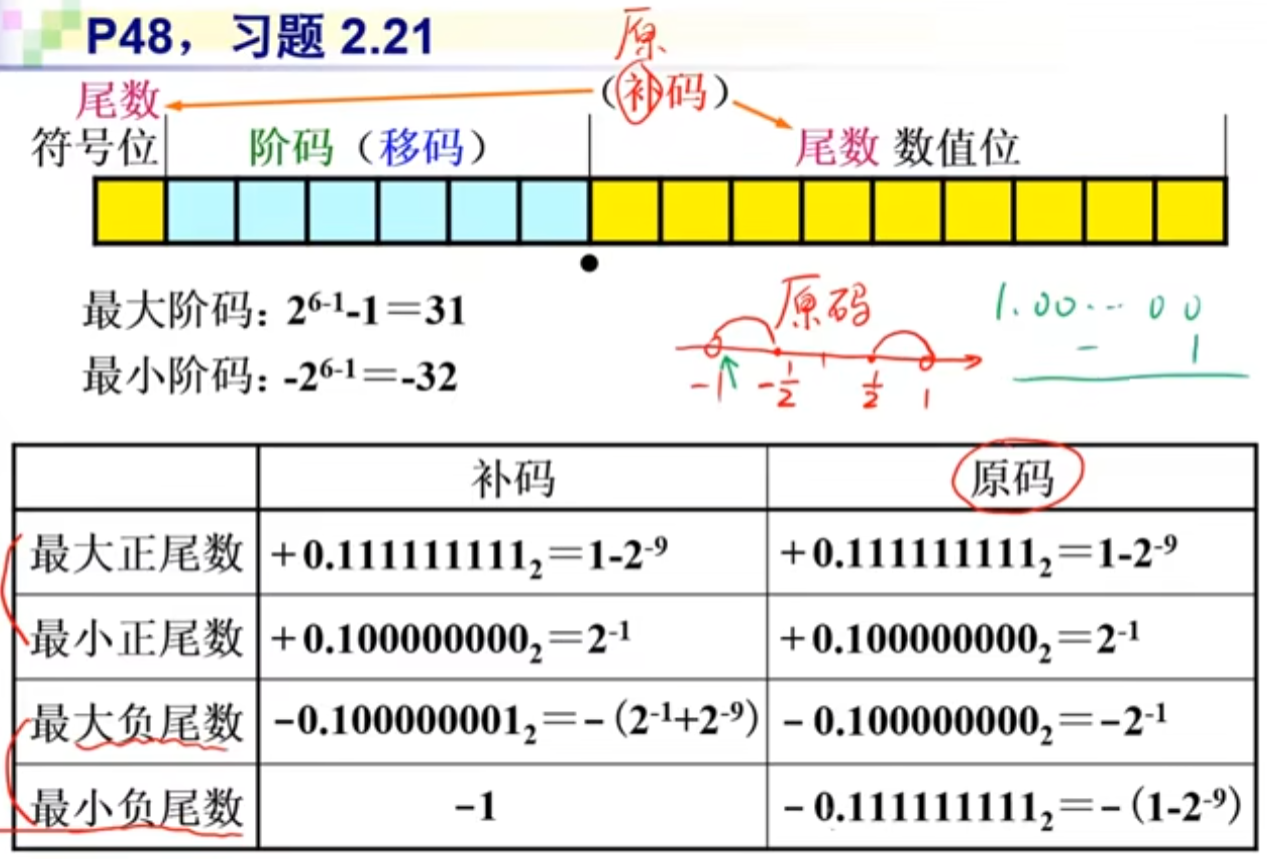
尾数用原码表示和尾数用补码表示两种方法尾数真值取值范围的对比:

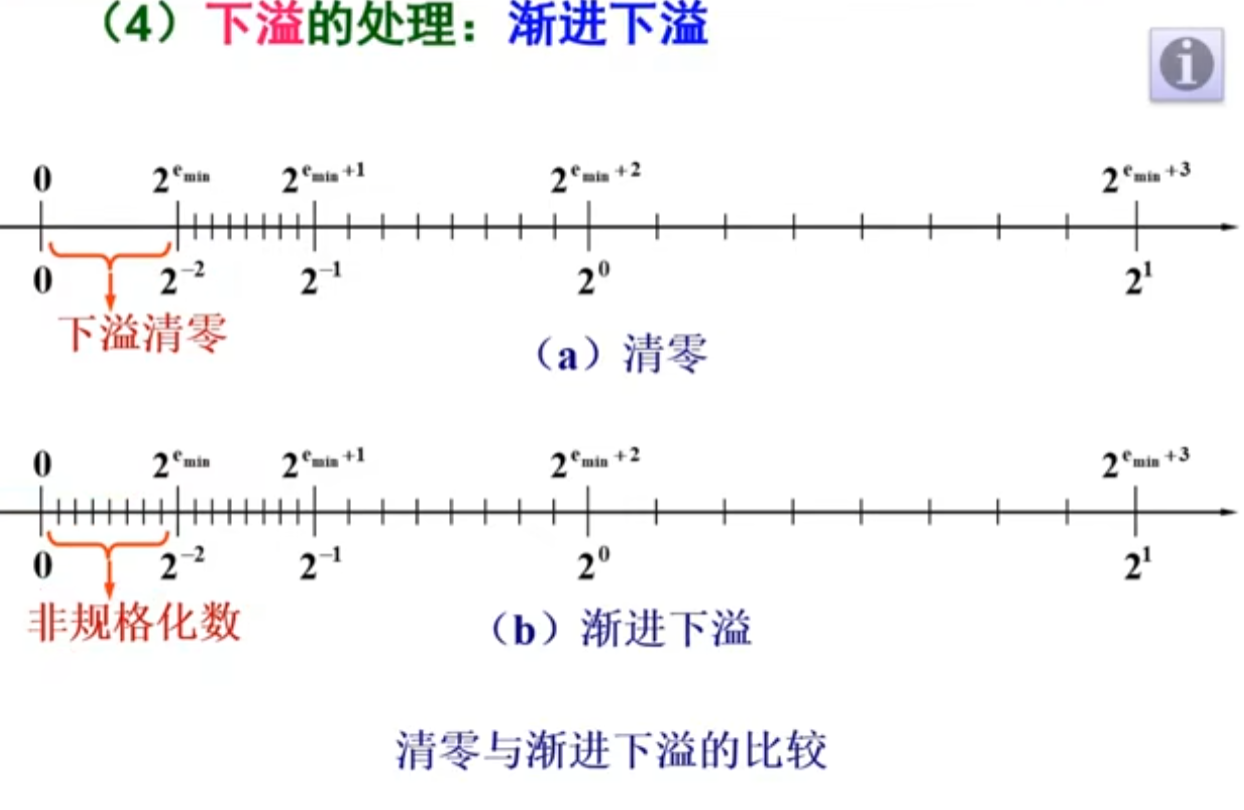
目前存在的一个问题:无法表示浮点数的0,只能表示一个十分接近0的数。后面IEEE754标准会解决这个问题。




关于为什么需要两个符号位,这是称之为变形补码,在计算机运算过程中为了防止溢出会有这种形式,但是运算结果只能是一个符号位。
3、浮点数的特点
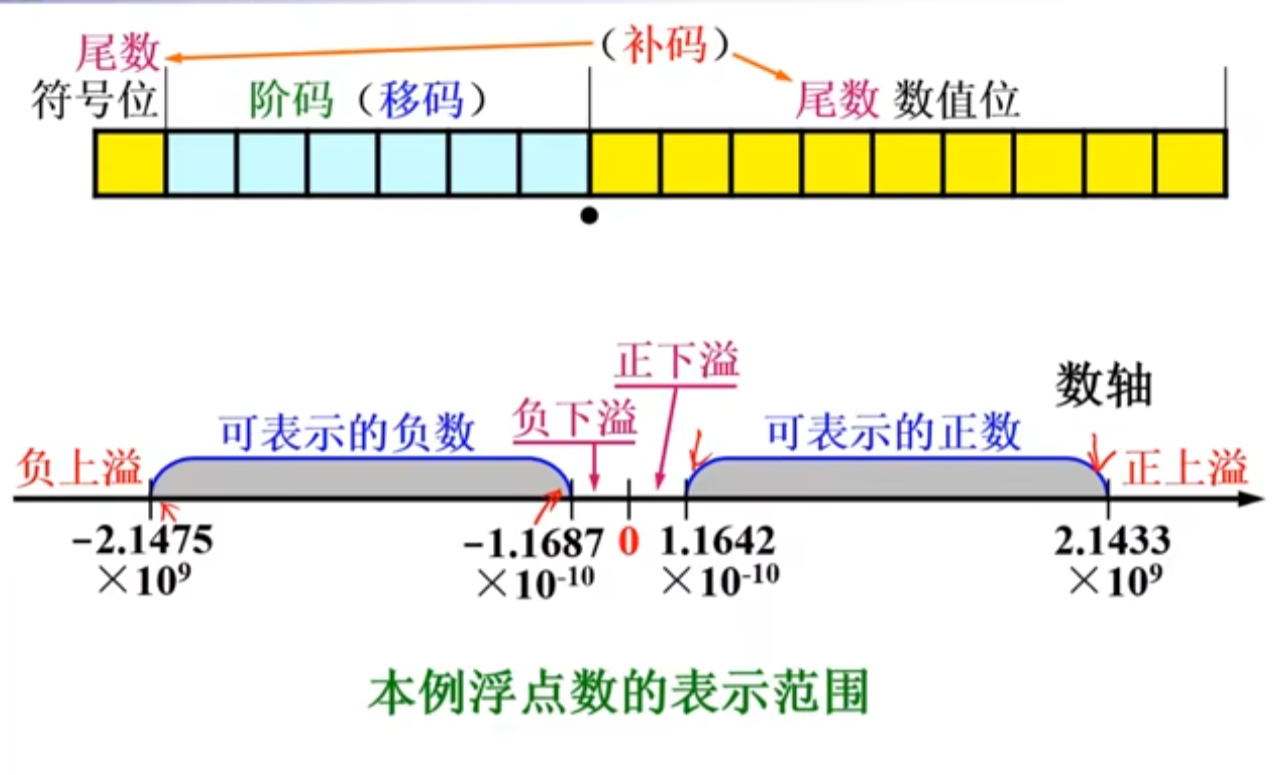
虽然浮点数的表示范围相对于定点数要大得多,但是一定的位数能表示的数字个数是有限的,比如一个32位的数,它只有-231~231-1这232种组合,也就是不管定点数还是浮点数最多只能表示232个。

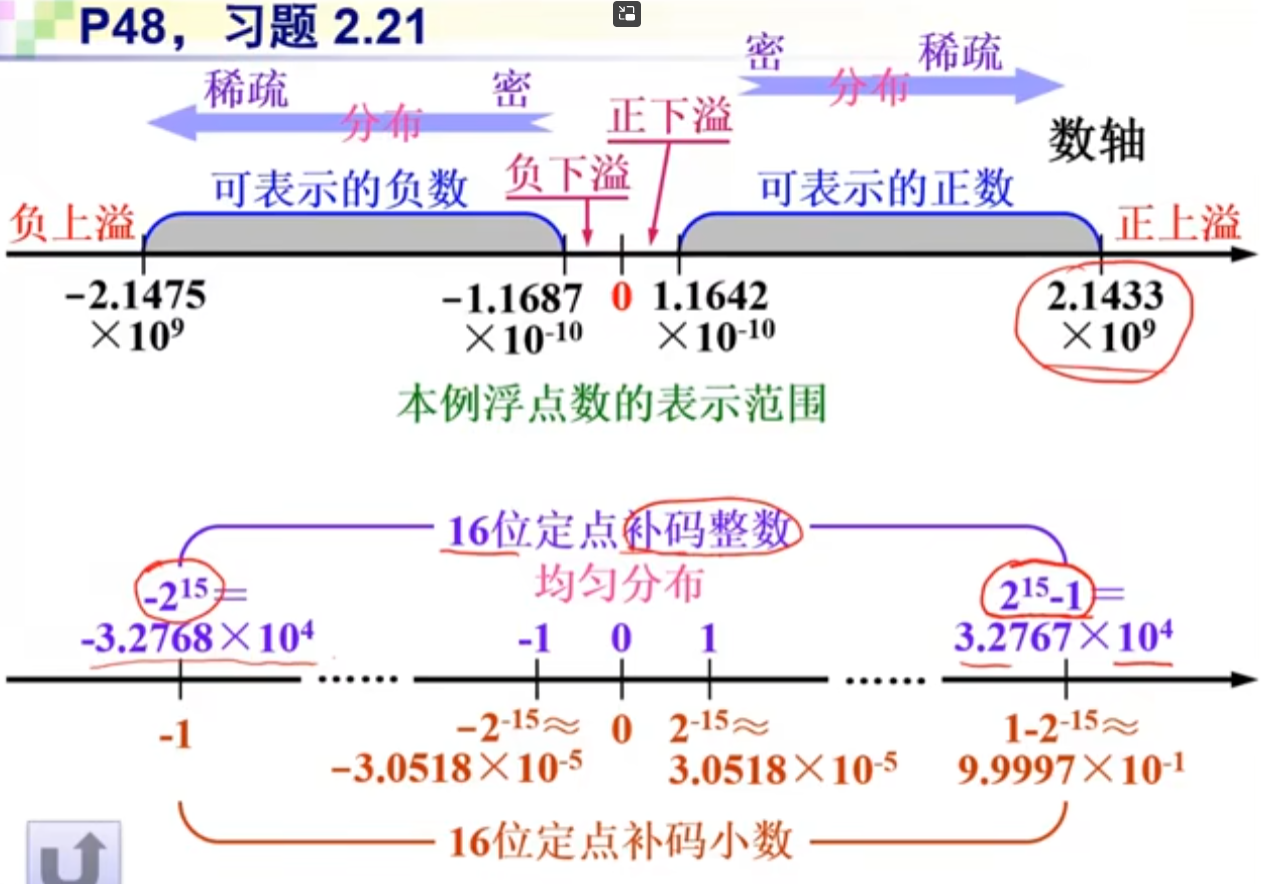
浮点数在数轴上的分布特点:离原点越近,分布越密,离原点越远,分布越稀。但两个相邻的2的整数次幂之间的数的分布是均匀的。
容易想到,定点数在数轴上应该是均匀分布。



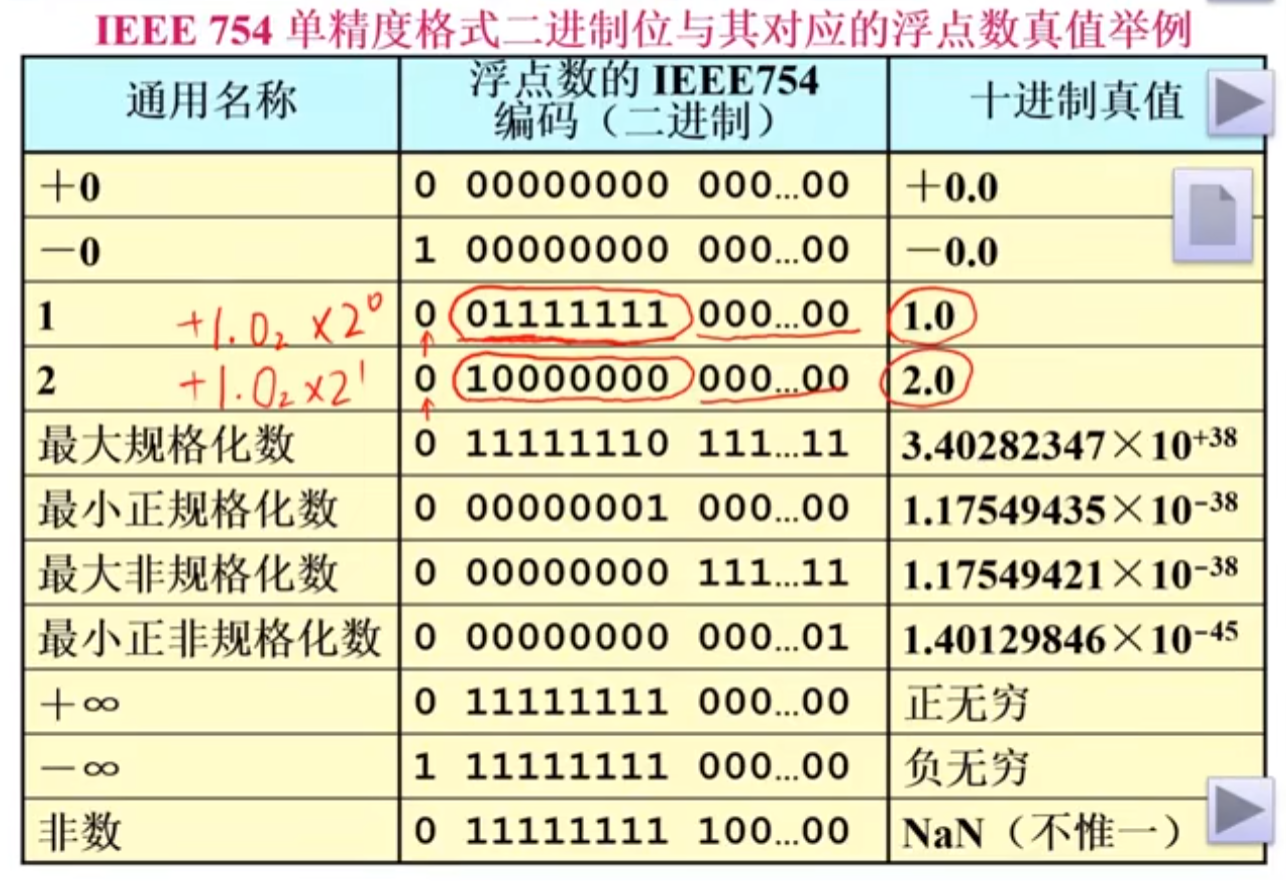
4、IEEE754标准

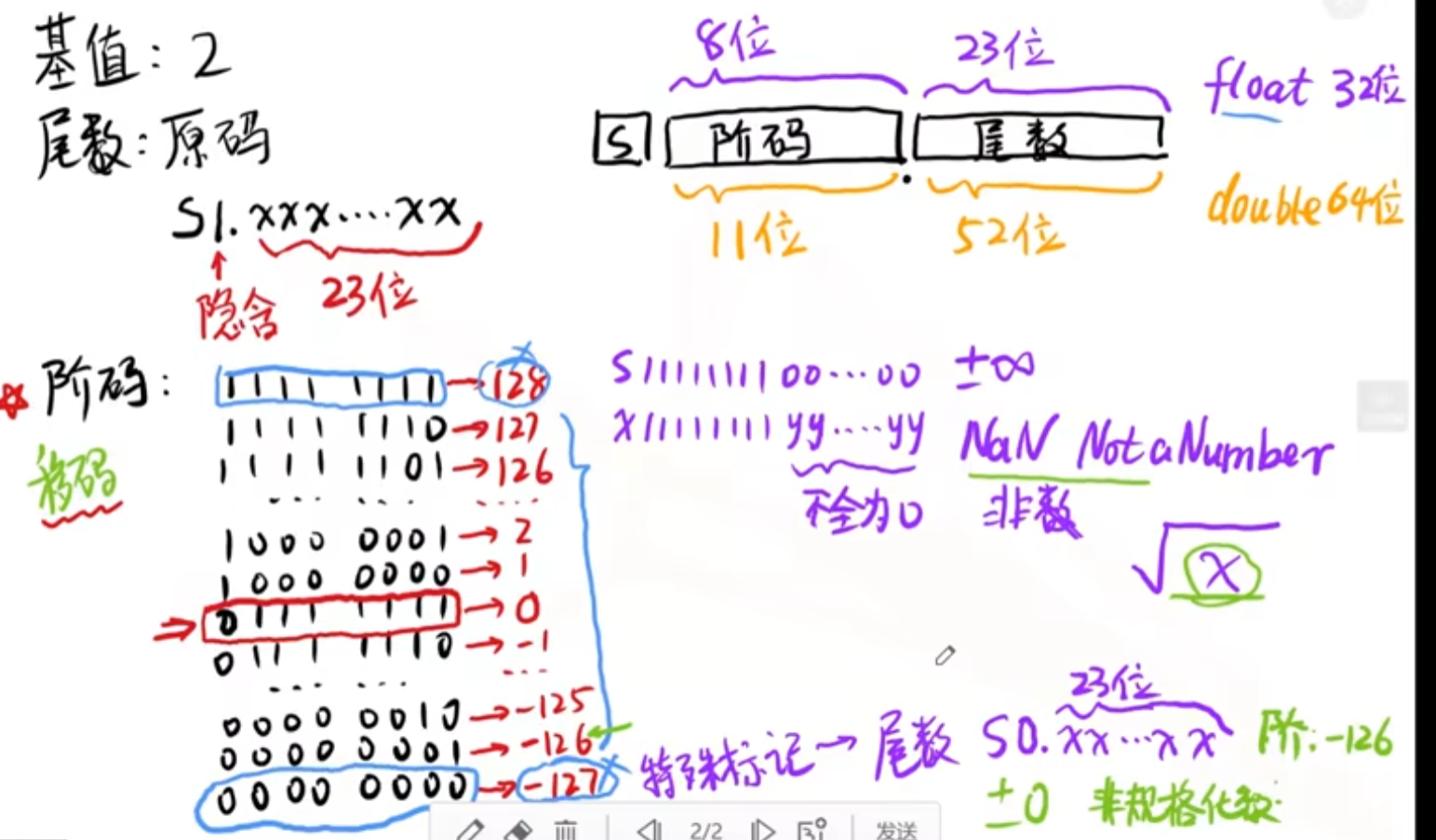
移码偏移量和之前不一样是为了正数比负数多一个数,从而在执行倒数运算时不会产生上溢,比如一个数的-126次方的倒数会有正的126次方与之对应。而下溢很好处理,可以近似为0,也可以使用非规格化数来表示。




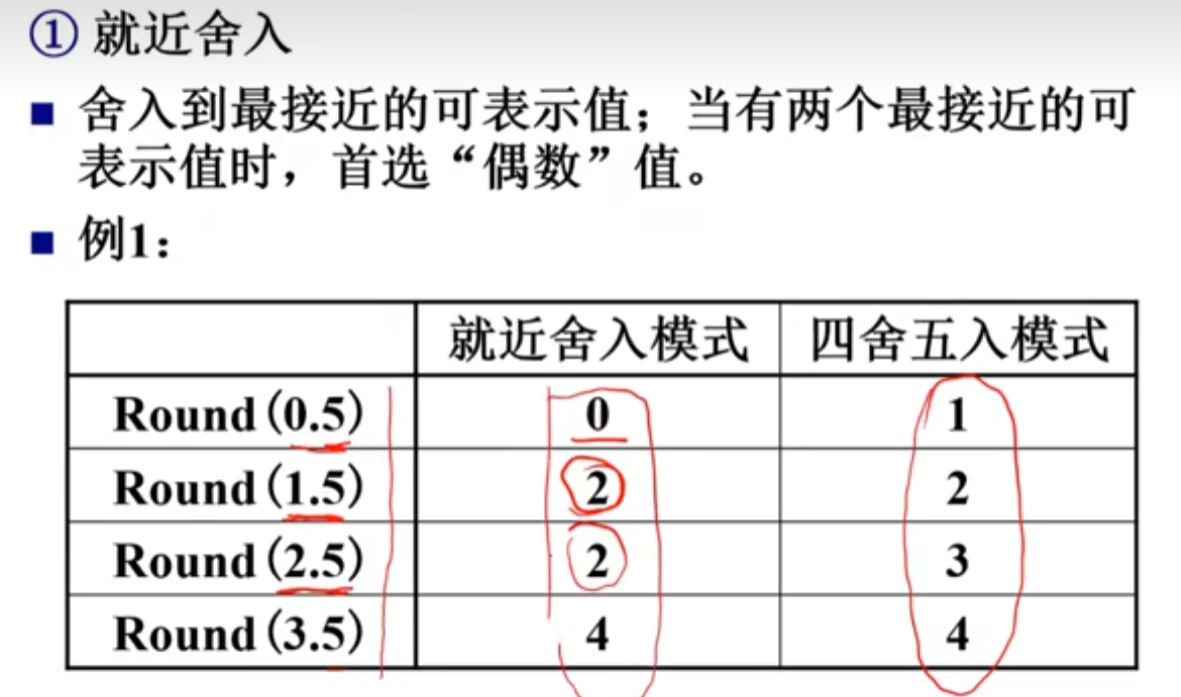
只有需要舍的数正好为5时这样舍入,其他如1.3、1.8还是按照四舍五入。
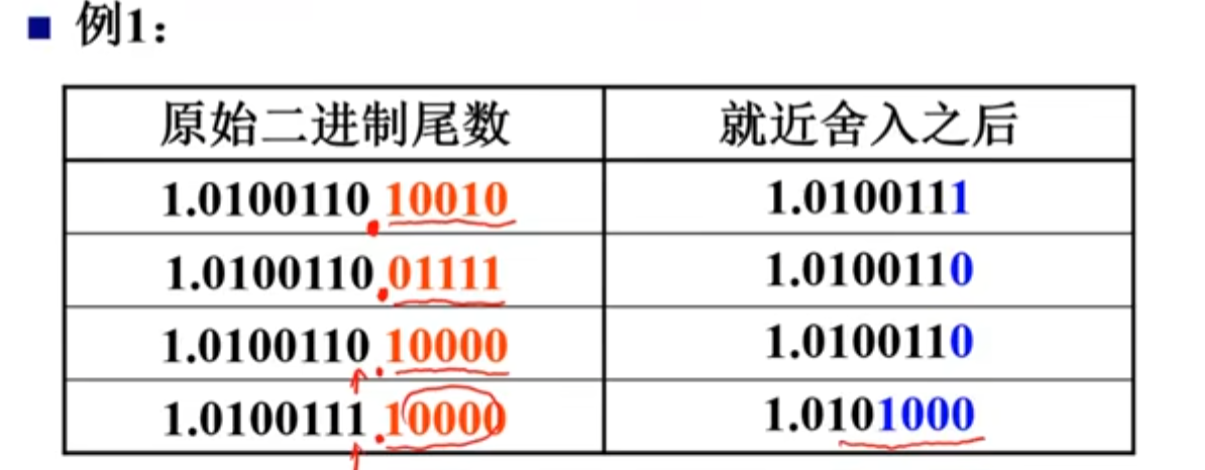
对于二进制来说就近舍入碰到“5”这种情况也就是留下的最后一位舍入后应为0






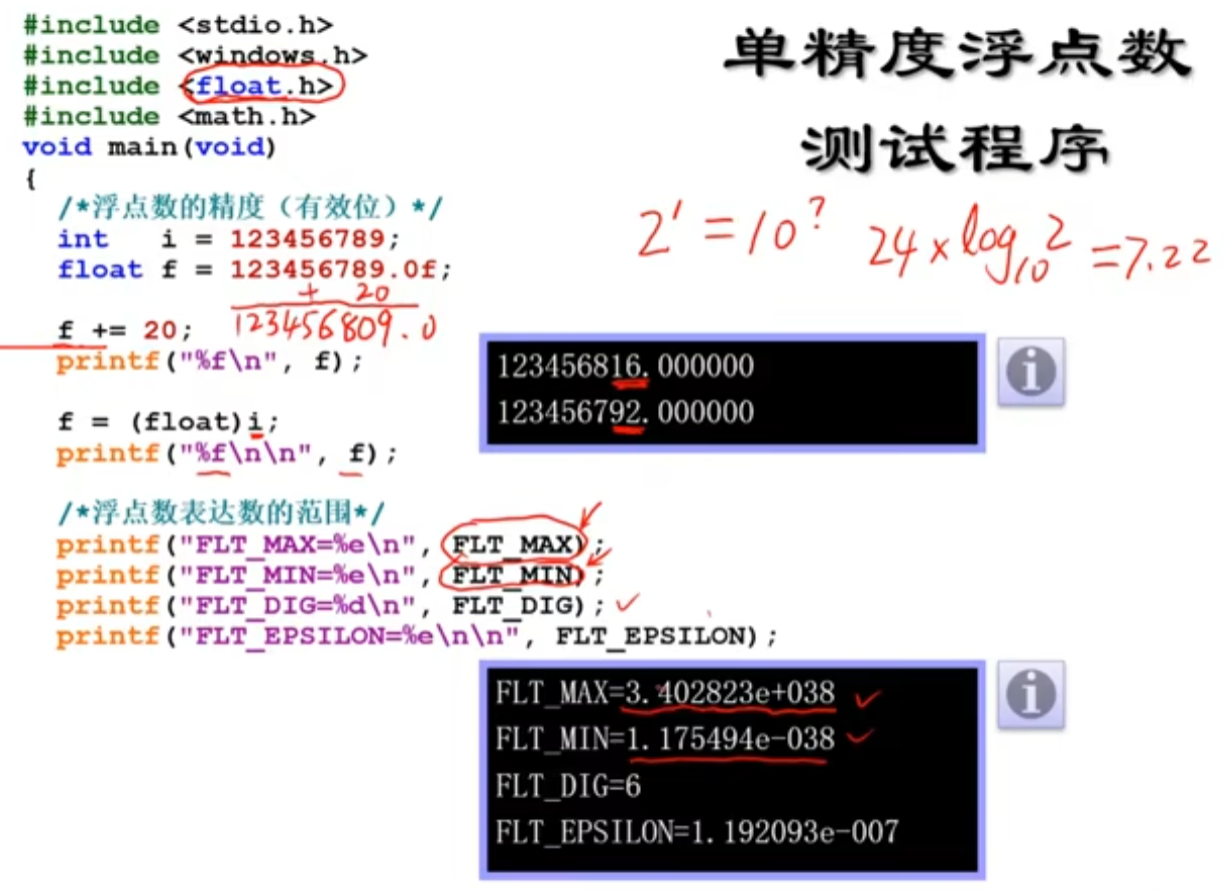
IEEE754标准下float只有23位尾数,可以表示最多24位的尾数,对应的最大值对应十进制应该时24lg2约等于7.所以上面程序中的数字只有前七位是准确的,后面两位不准确。
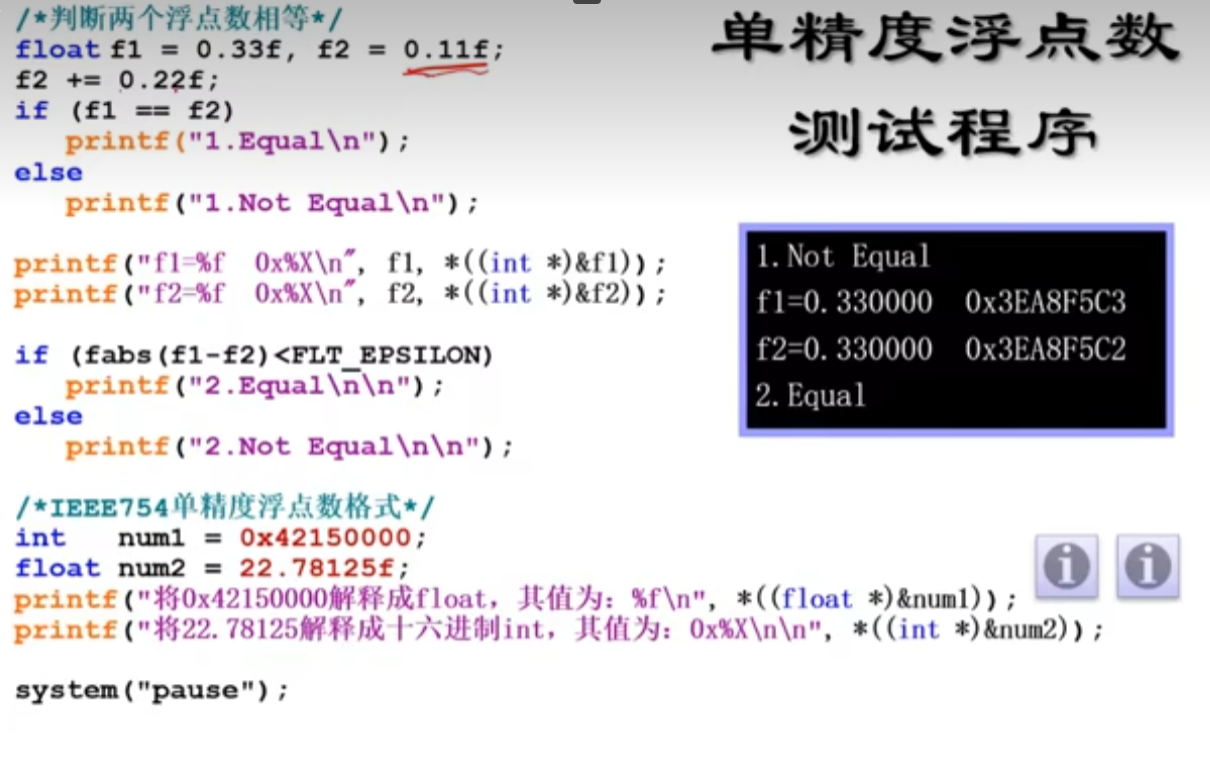
0.22和0.11在转换成单精度浮点数时会有精度损失。
三)二进制编码的十进制数

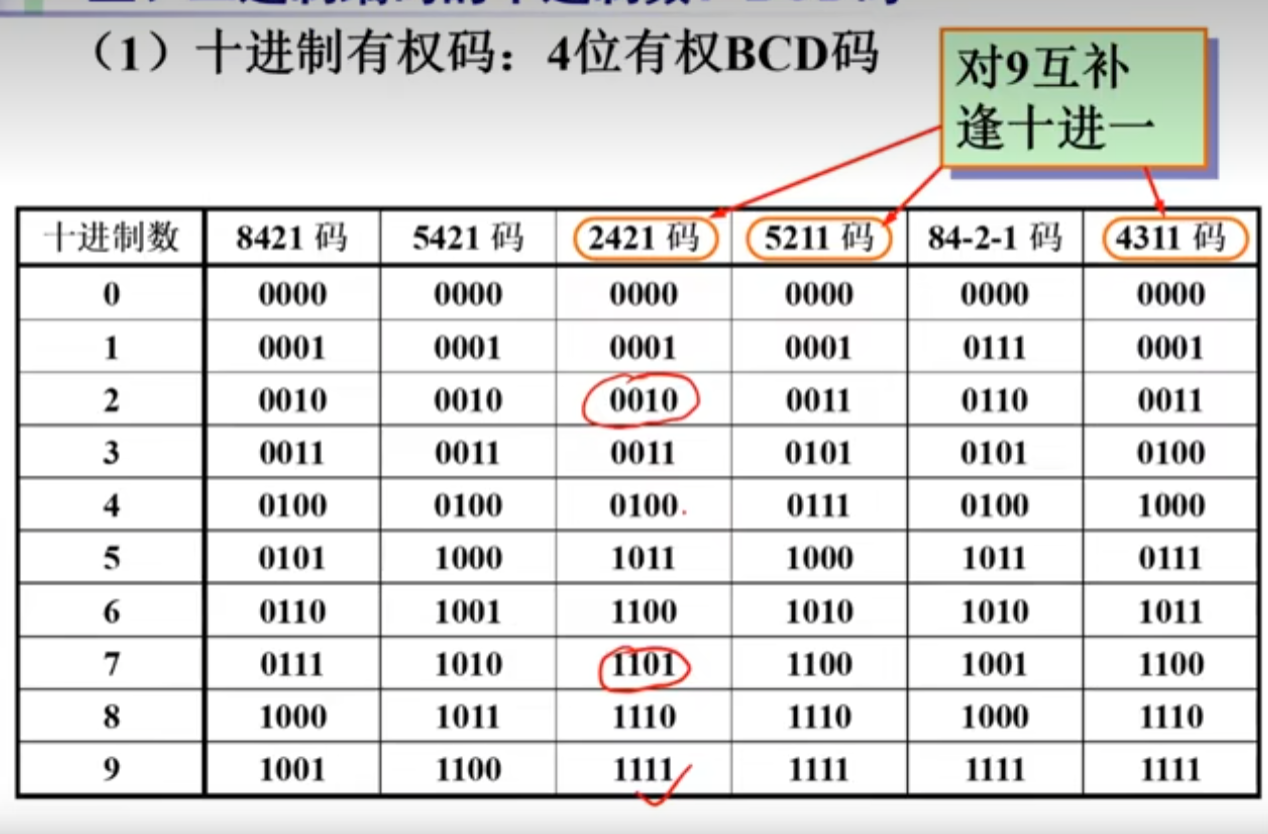
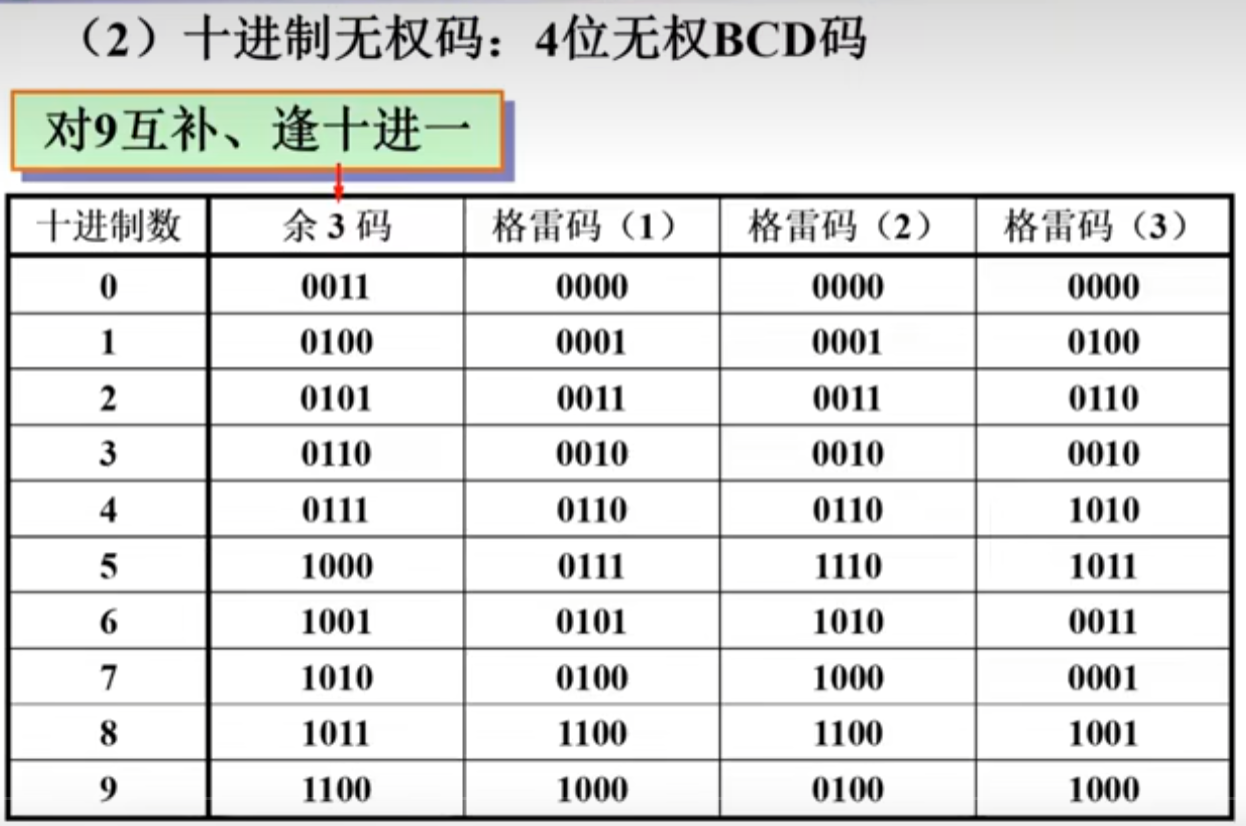
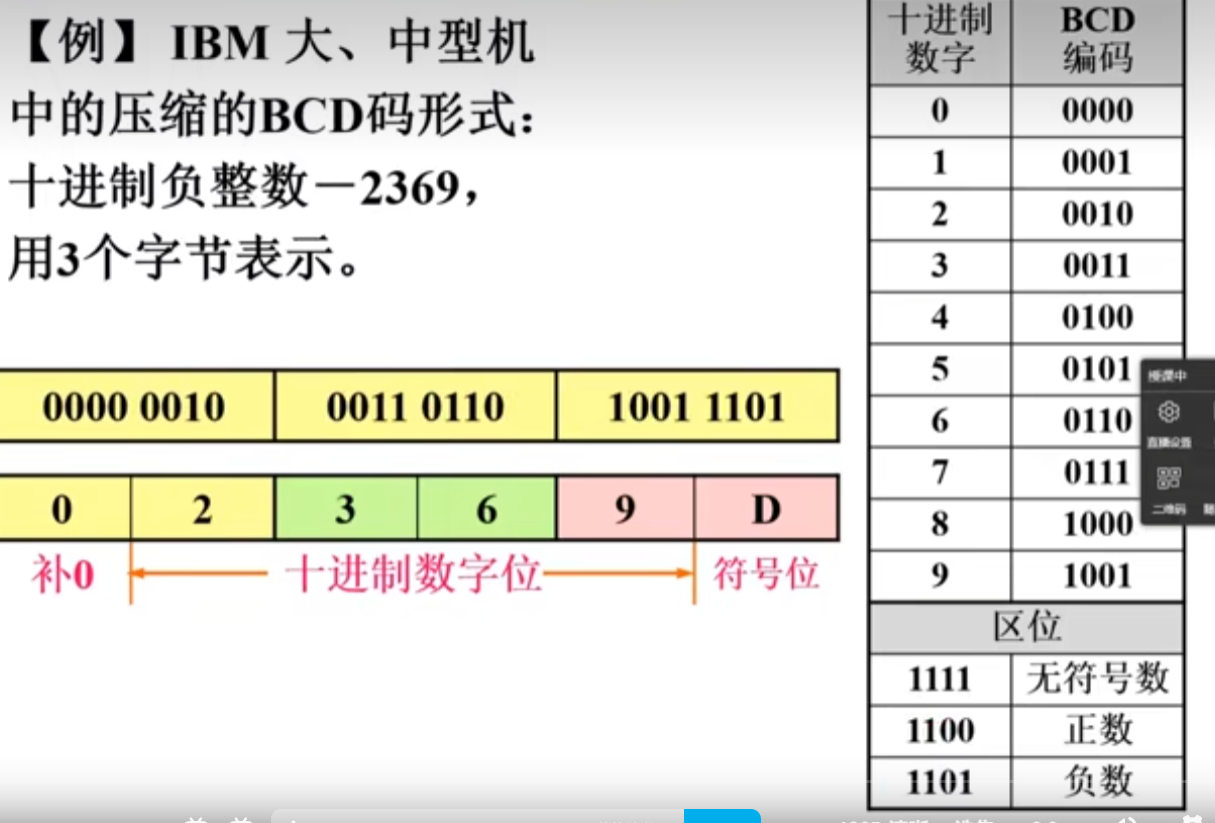
四)非数值数据的编码


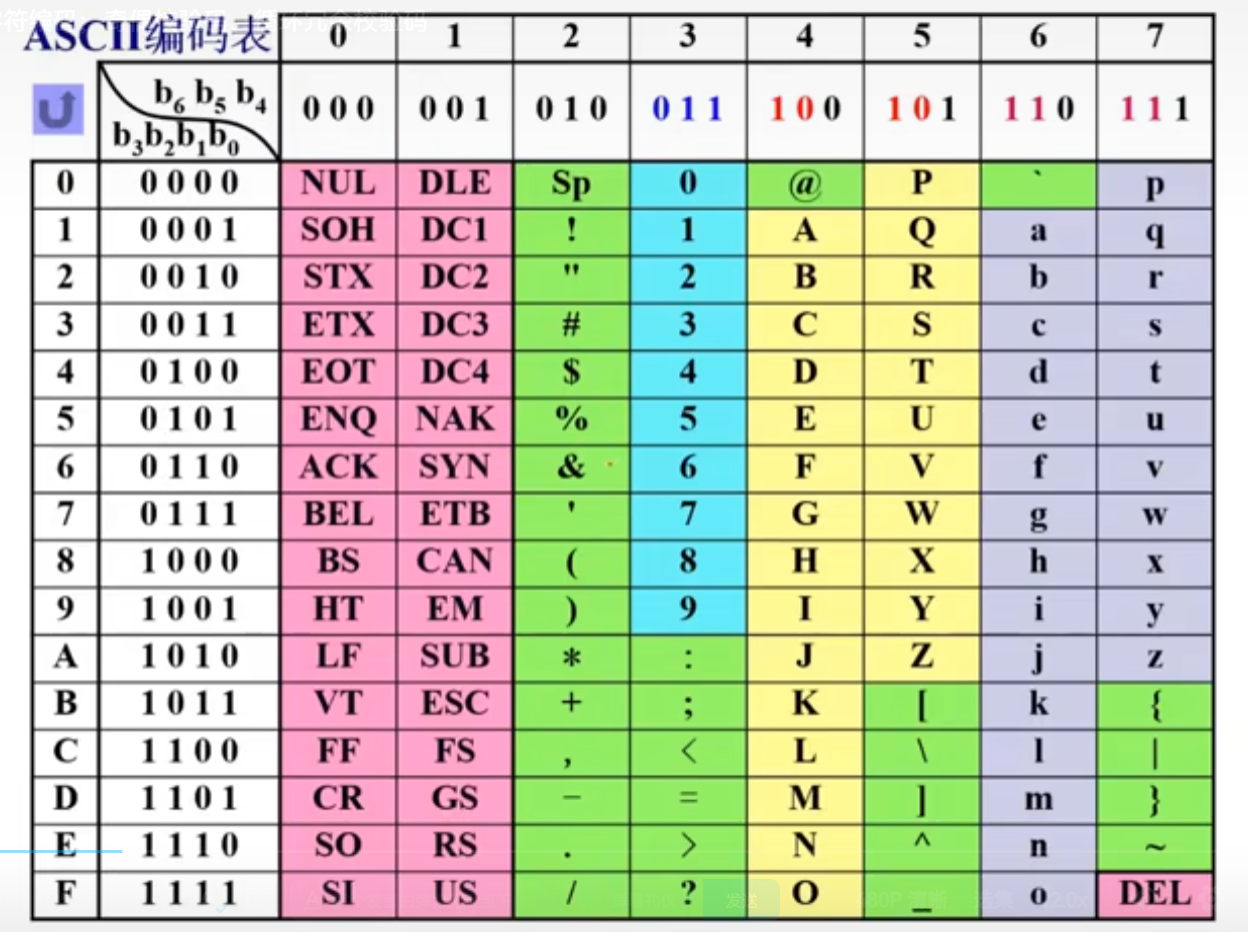
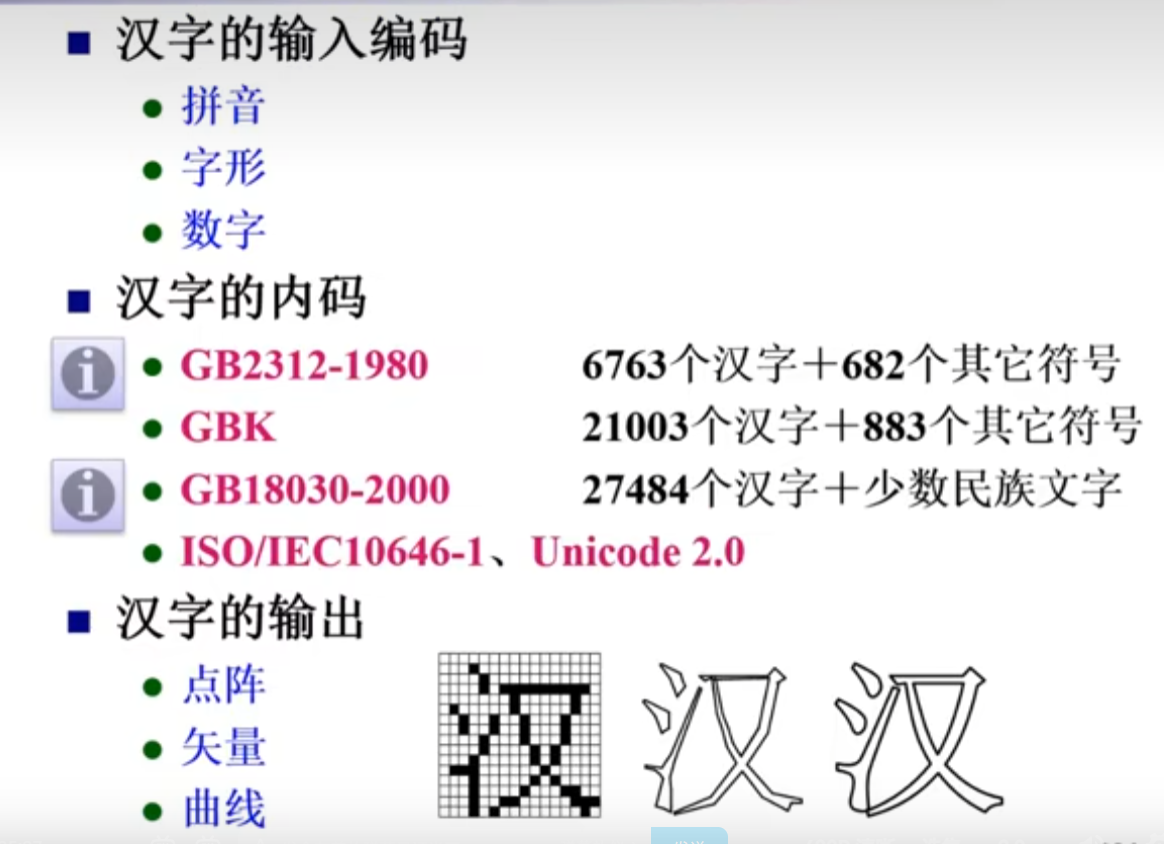
前两种是两个字节表示。

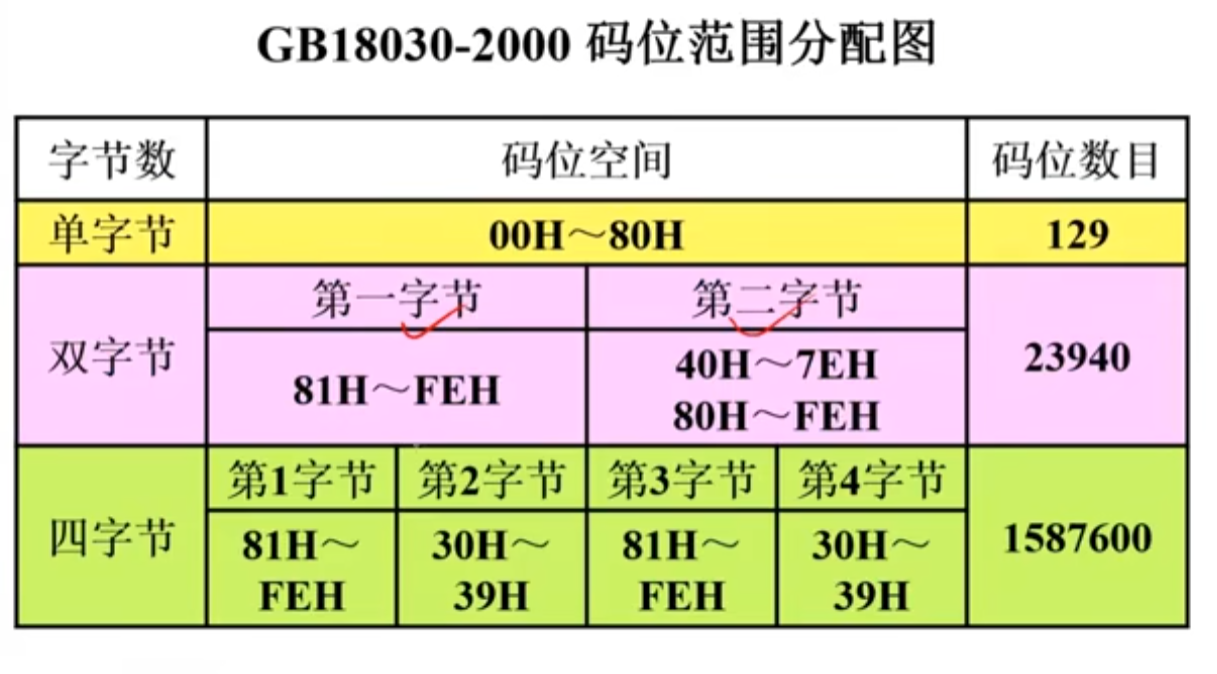
常用字用两个字节表示,生僻字用四字节表示。
五)检错与纠错码


1、奇偶校验码



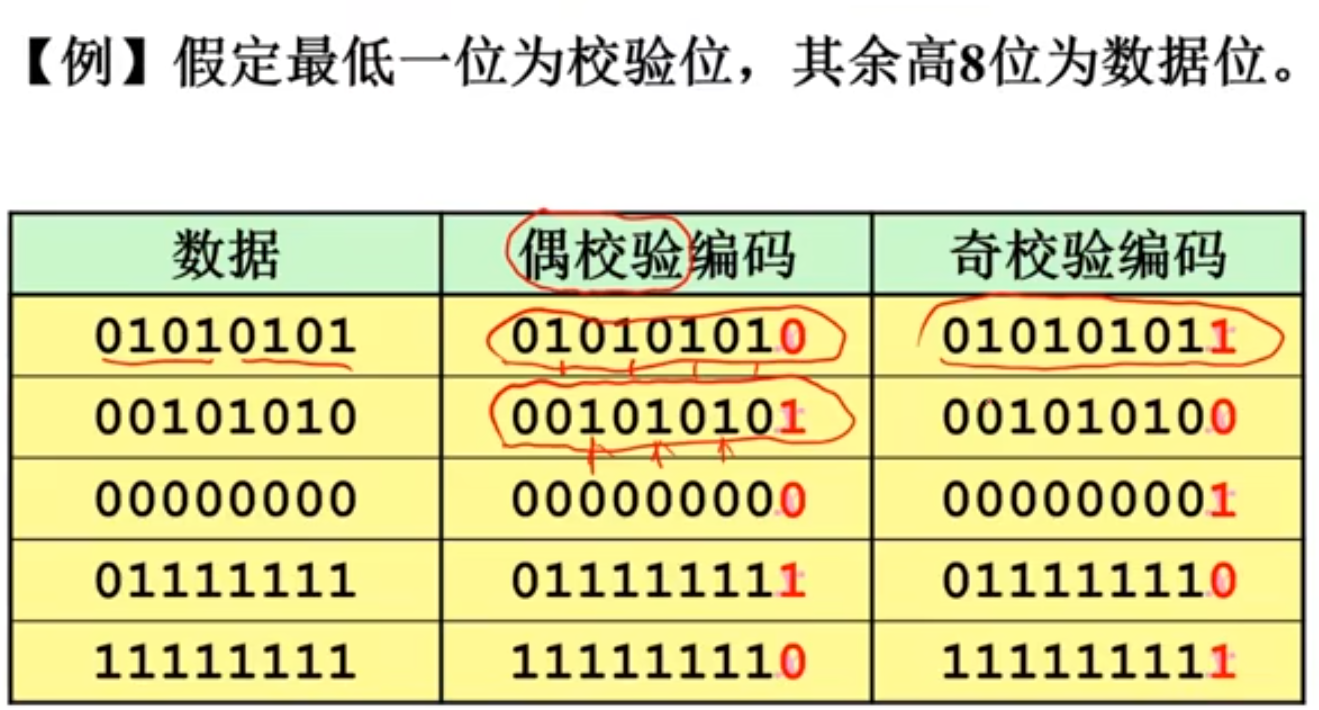

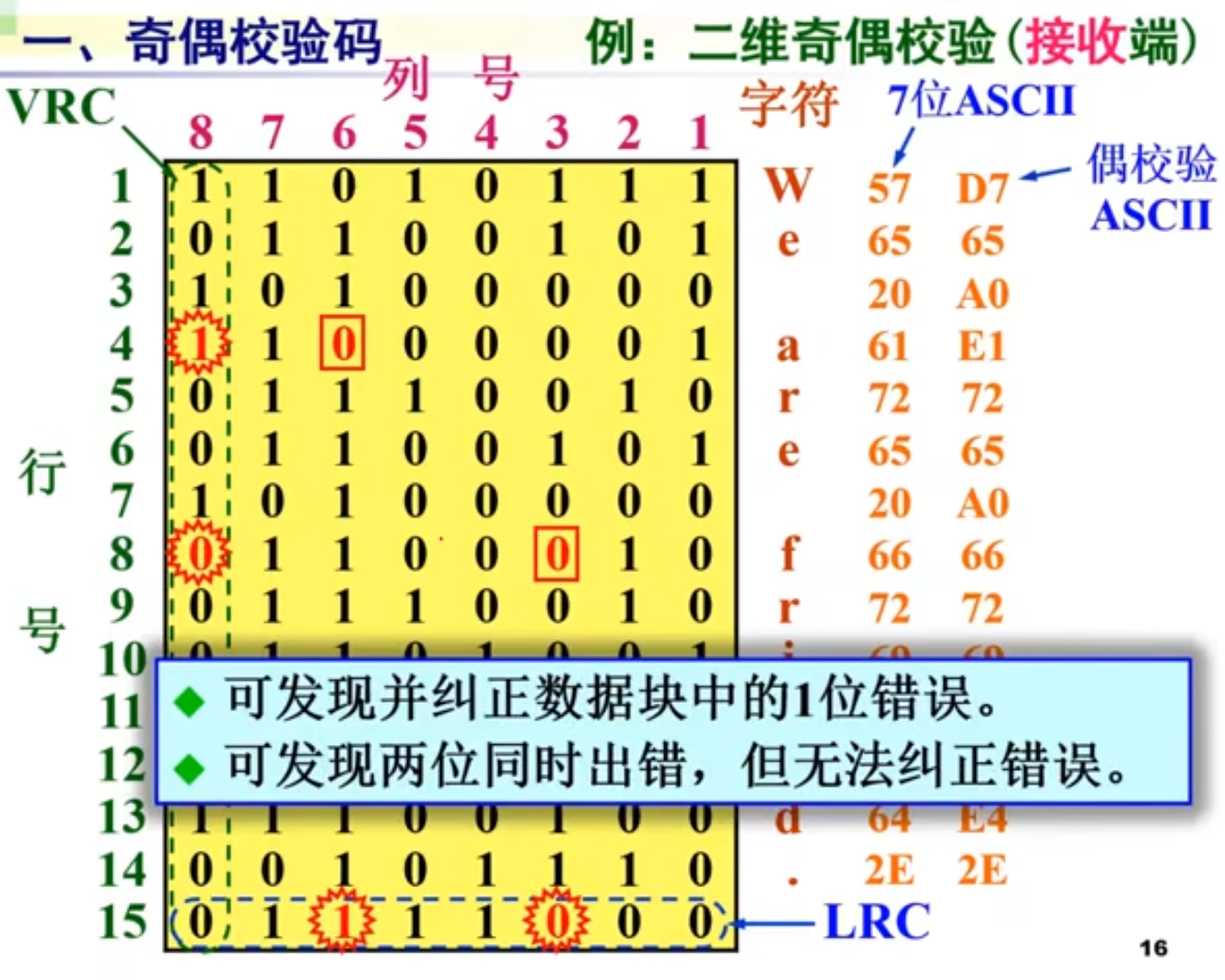
也可以发现三位错误,但不能发现四位。
2、循环冗余校验码(CRC)



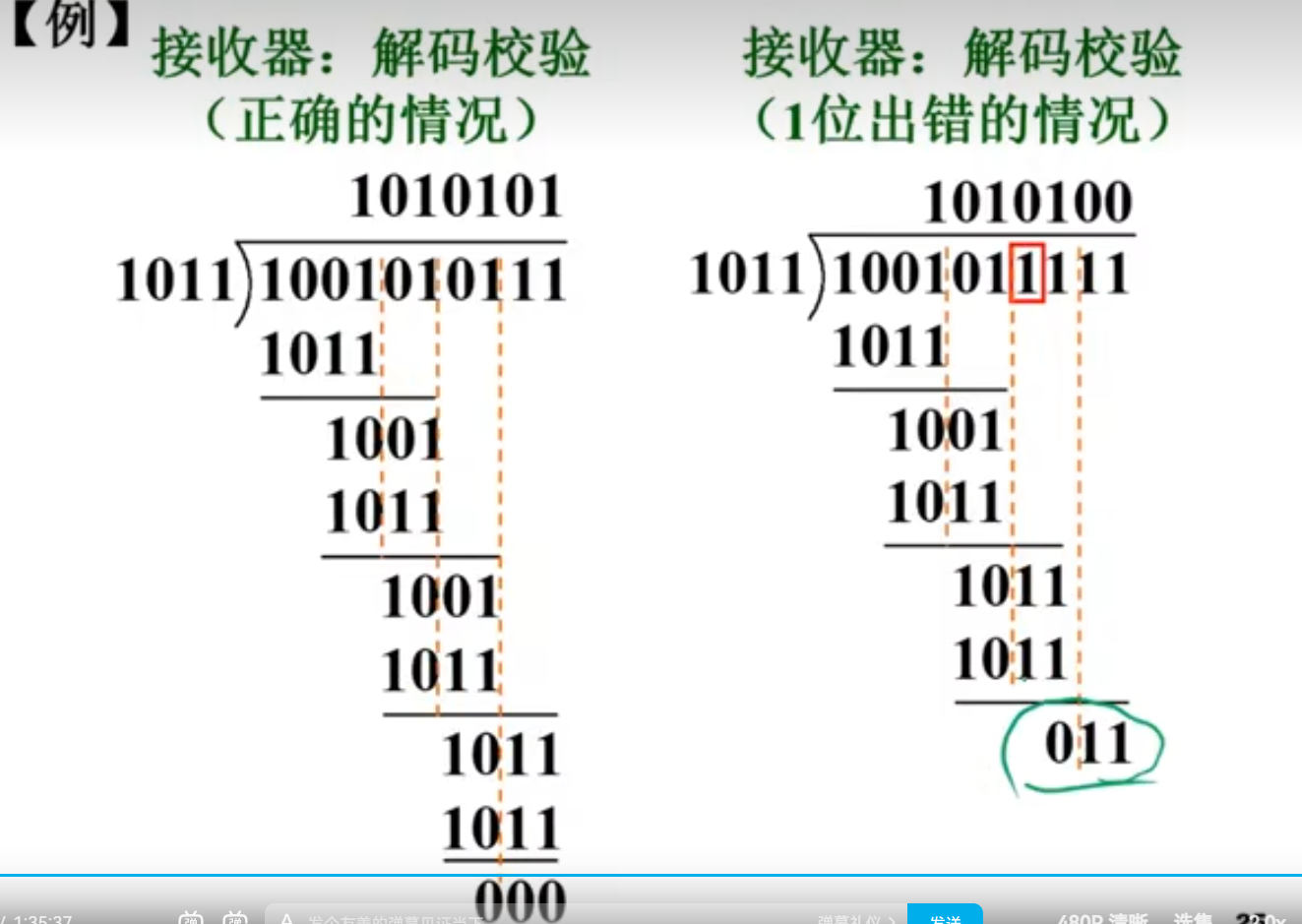
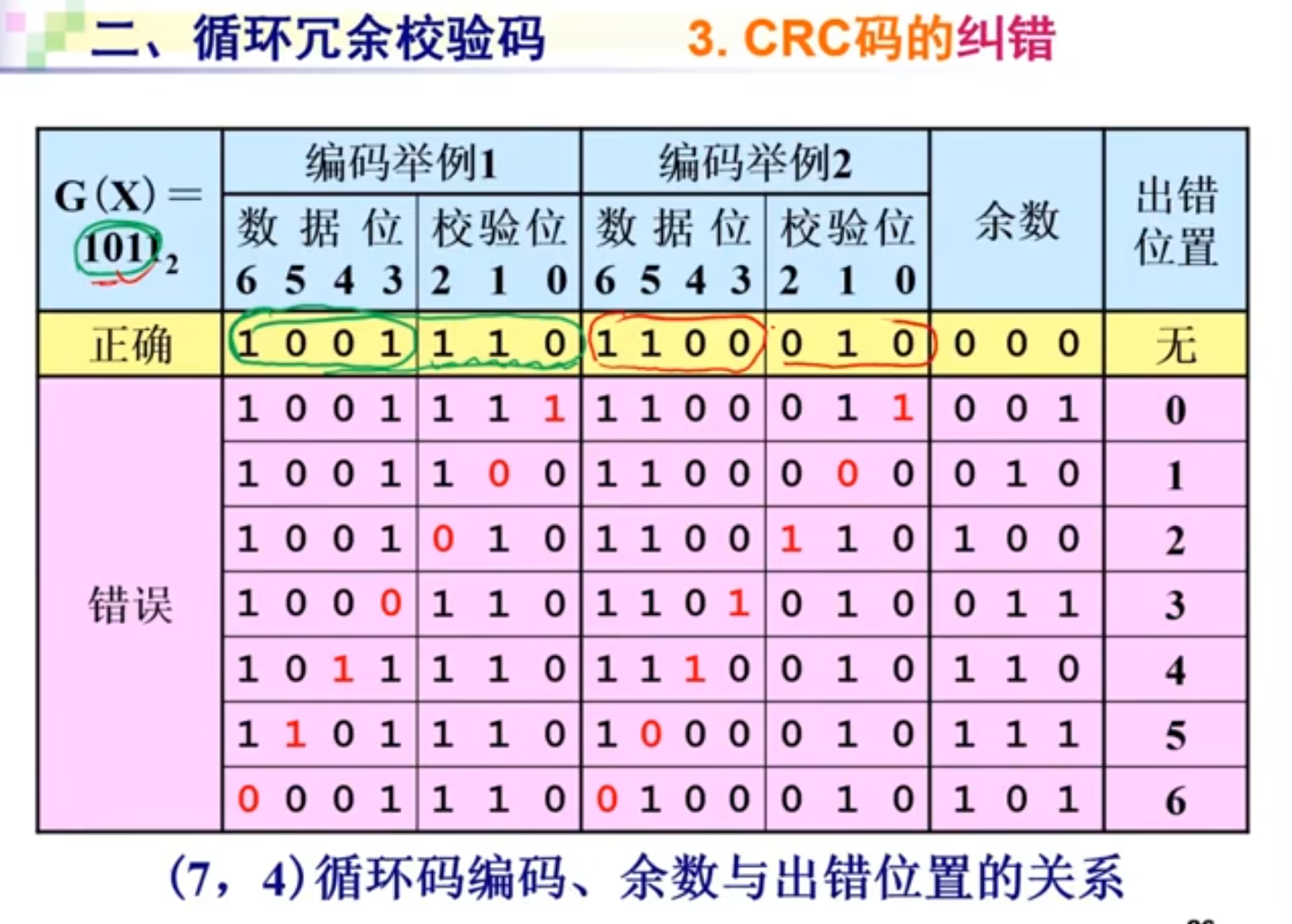

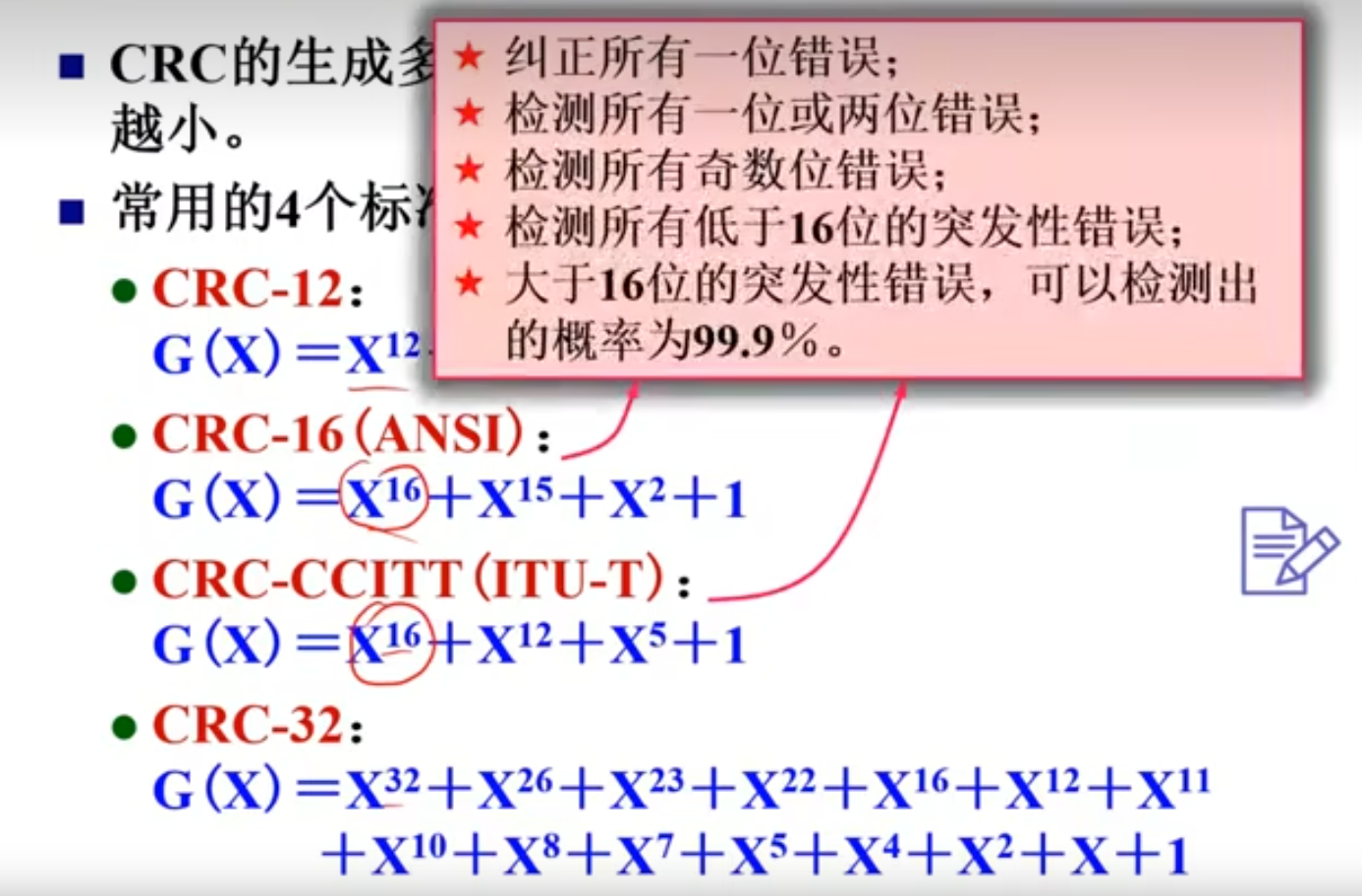
3、海明码

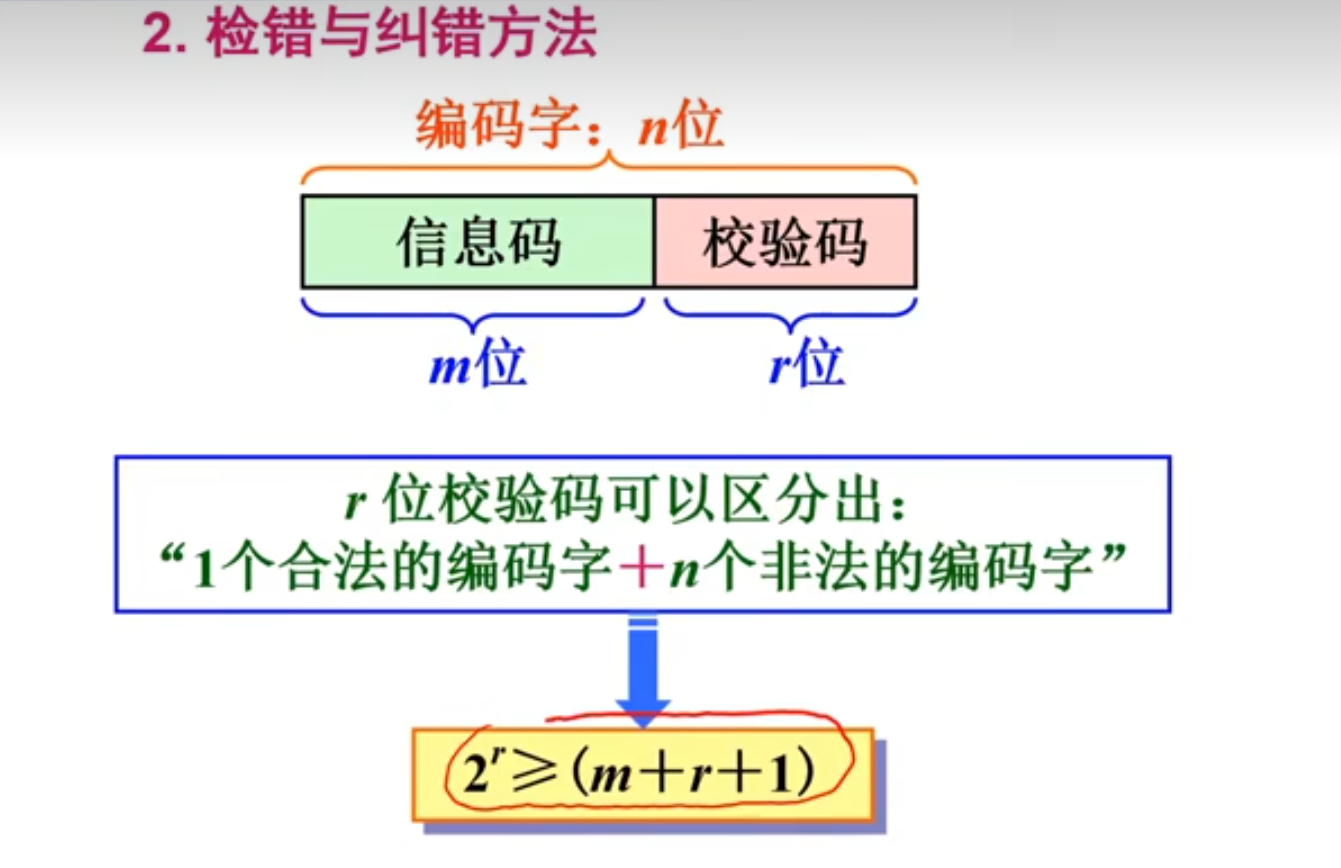
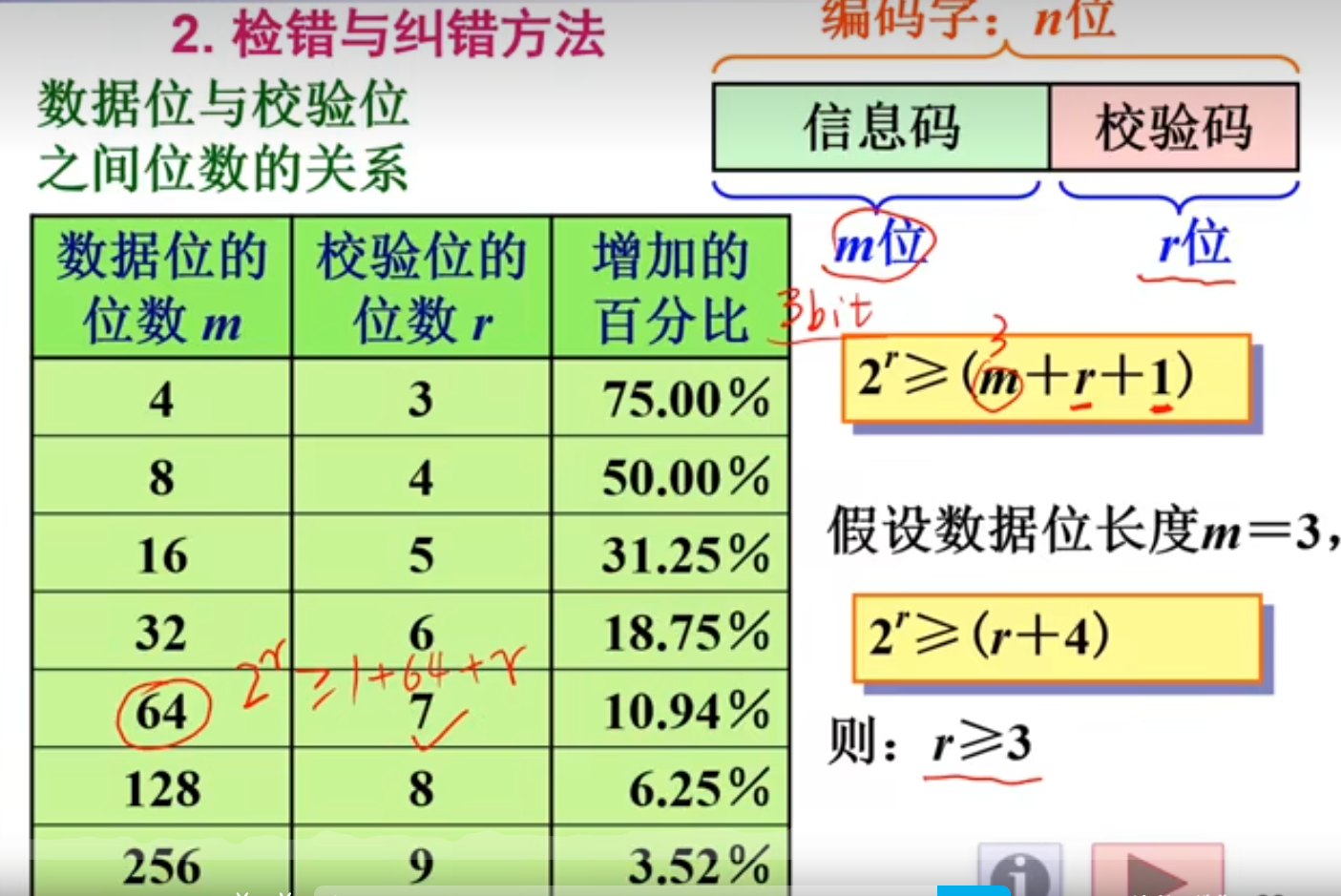

海明码可以检测1或2位错误,只能纠正一位错误。
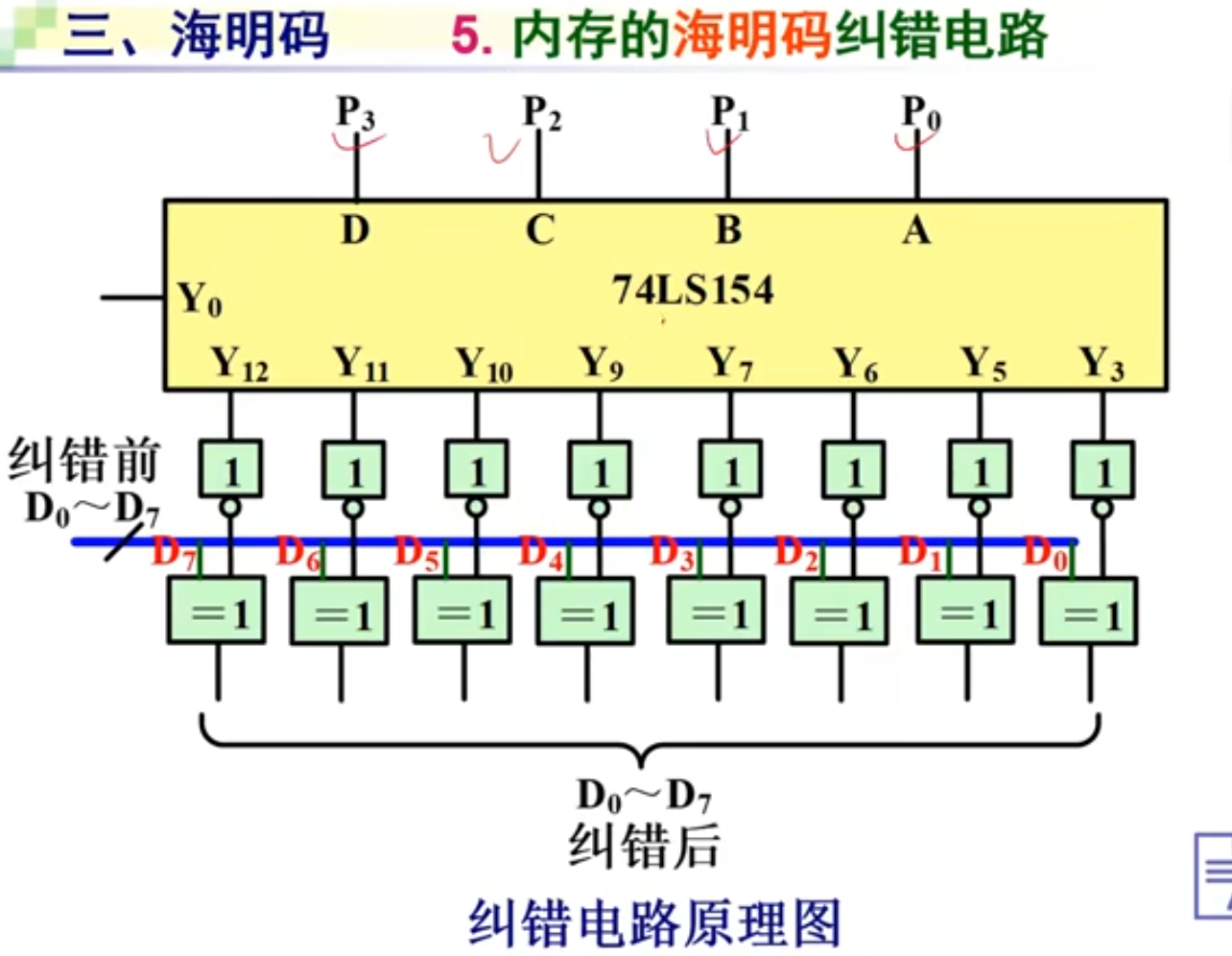
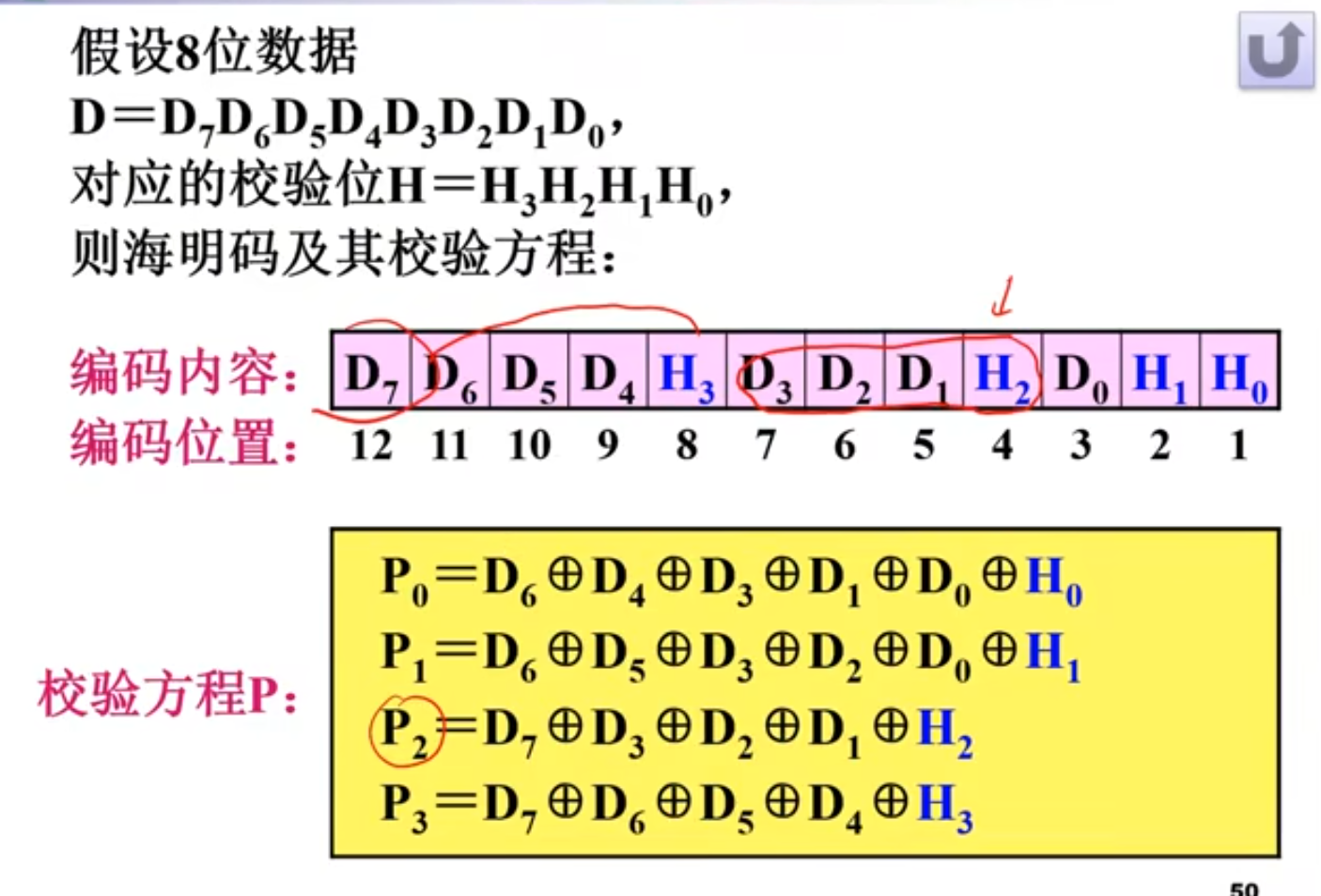
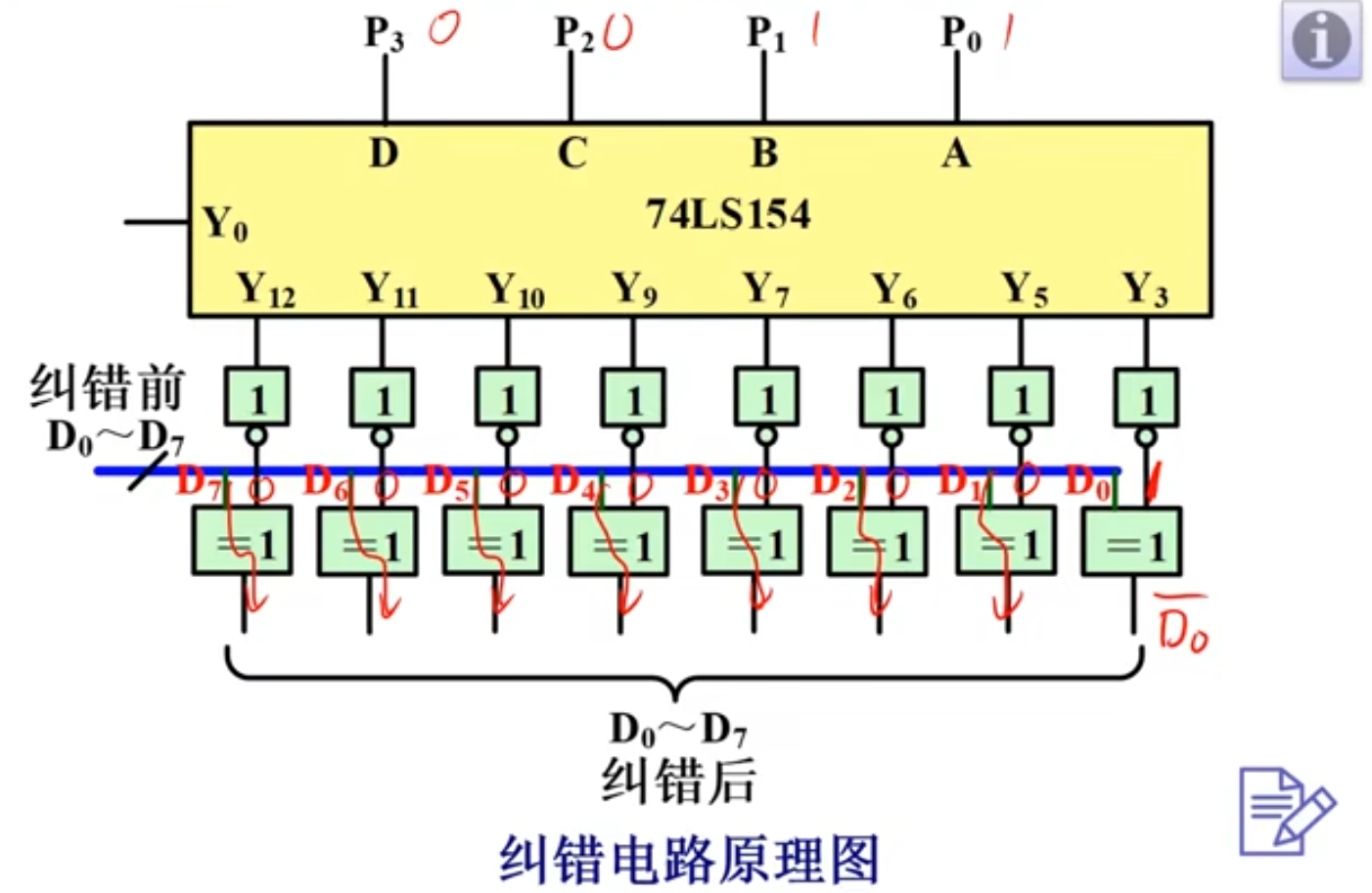
本文来自博客园,作者:Athonal0,转载请注明原文链接:https://www.cnblogs.com/athonal0/p/17333093.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号