数学分析(3)
1.多元函数的极限与连续
1.平面点集与多元函数
邻域:\(\delta\) 圆邻域和 \(\delta\) 方邻域,视情况而选用
内点: 有邻域能够在 \(E\) 内
内部:全体内点的集合
外点:有完全不含于 \(E\) 的集合
界点:所有邻域都能同时包含属于 \(E\) 和不属于 \(E\) 的点
\(\delta E\):边界,即所有界点构成的集合
聚点:任何 空心 邻域都含有 \(E\) 的点 \(\Leftrightarrow\) 任何邻域含有 \(E\) 的无穷个点
孤立点:属于 \(E\) 但不是 \(E\) 的聚点的点
这里有,因为孤立点本身是属于 \(E\) 的,而会有邻域不包含 \(E\) 的点,且可以想象这个邻域在所有邻域中处
于内环的位置,所以孤立满足界点的定义
开集:每一点都是 \(E\) 的内点,保证了边界上的点不被取到
闭集:所有聚点都属于 \(E\),保证了边界上的点都能被取到
特例:没有聚点时也称为闭集
开域:非空连通开集
闭域:开域连同其边界
这里描述了闭域是开集加上边界,那么闭域是否等同于闭集呢?
我们看到闭域满足闭集的定义,所以闭域一定是闭集
但是对于闭集,考虑例子
{\({{(x,y)|x^{2} + y^{2}=1或y=0,0 \leq x \leq 1}}\)}
这是一个闭集,因为圆弧附近同样有无穷多个点,但是却无法用含于 \(E\) 的线段连接,因此不是闭域
柯西准则:
必要性:三角不等式
充分性:\(x\) 坐标和 \(y\) 坐标这两个子列收敛
闭域套定理:
用柯西准则,当邻域直径趋于无限小时,两点间距离趋于 \(0\),从而收敛于某一点,这一点即被套住的点
聚点定理:设 \(E\subset R^{2}\) 为有界无限点集,则 \(E\) 在 \(R^{2}\) 中至少有一个聚点
有限覆盖定理
2.二元函数的极限
二元的海涅归结原则: 任意找一个以 \(P_{0}\) 为聚点的子集,它的极限是 \(A\) \(\Leftrightarrow\) 在整个集合上点的极限是 \(A\)
由这一原则可以得到如下推论:
-
子集趋于聚点的极限不存在,则整个集合趋于聚点的极限也不存在
-
两个子集趋于聚点的极限存在但不相等,则整个集合趋于聚点的极限也不存在
-
\(lim f(p)\) 存在 \(\Leftrightarrow\) 对于所有趋于 \(P\) 的子列 \(P_{n}\) , \(f(P_{n})\)都收敛
累次极限:\(x、y\) 分先后趋于点 \(P\)
重极限:\(x、y\) 同时趋近于点 \(P\) 的横纵坐标
| 定理:若累次极限和重极限均存在,则两者相等
proof: 因为累次极限是可以固定一个坐标不动,让另一个坐标取极限的 我们先假设重极限为 \(A\) 用数学语言就是 \(\forall \epsilon > 0,\exists \delta > 0 ,使|f(x,y)-A|<\epsilon\) 此时点位于以 \(\delta\) 为半径的邻域中 所以自然也有 \(|x-x_{0}|<\epsilon\) 对于这一区域的每个 \(x\),都有 \(\lim(y \to y_{0})\)时,\(f\) 能取得极限 \(\phi(x)\) 在最初的不等式中再让 \(x->x_{0}\)即可 |
由此有两个推论:
-
两个累次极限和重极限都存在,则三者相等
-
两国累次极限存在但不相等,则重极限不存在
习题:
16.2(2)
累次极限不存在:因为固定的常数乘以不存在极限的 \(sin\)
重极限存在:考虑将原式放缩成 \(x+y\)
16.2(3)
重极限考虑\(f(x,x)和f(x,0)\)
16.2(7)
累次极限易证不存在
重极限:令\(y=kx^{2}\)
然后将原式拆成\(\frac{e^{kx}-e^{y}}{ky^{2}}\cdot \frac{ky^{2}}{sin(ky^{2})}\)
其中第二部分是一个常见极限,再对第一部分用洛必达即可发现此极限与 \(k\) 相关
4
取 \(\delta = \epsilon\),然后将原式放缩成 \(x\),进而放缩成 \(\sqrt{x^{2}+y^{2}}\)
3.二元函数的连续性
一致连续性定理(存疑)
习题
16.3.1(2)
在\(k<x+y<k+1\)时连续,在\(x+y=k\)时不连续
(4)
在 \((0,0)\) 处把 \(\sin xy\) 放缩成 \(|xy|\),进而把整体放缩成 \(|x|\),从而趋于 \(0\)
(5) 存疑
取极限为 \(A\) 这里需注意 \(A \neq 0\)
然后再利用基本的极限形式,取 $\epsilon = A - r $ 即可
第一个条件固定 \(x\),使 \(y\) 可变,第二个条件固定 \(y\) ,使 \(x\) 可变,其中第二个条件中的“一致连续”保证了第
一个条件中固定下来的 \(x_{0}\) 是任意的
2.多元函数微分学
1.可微性
可微: f 在 \(P_{0}\) 处的全增量 \(\Delta z\) 可表示为 \(A\Delta x + B\Delta y + o(\rho)\)
偏导数的几何意义:
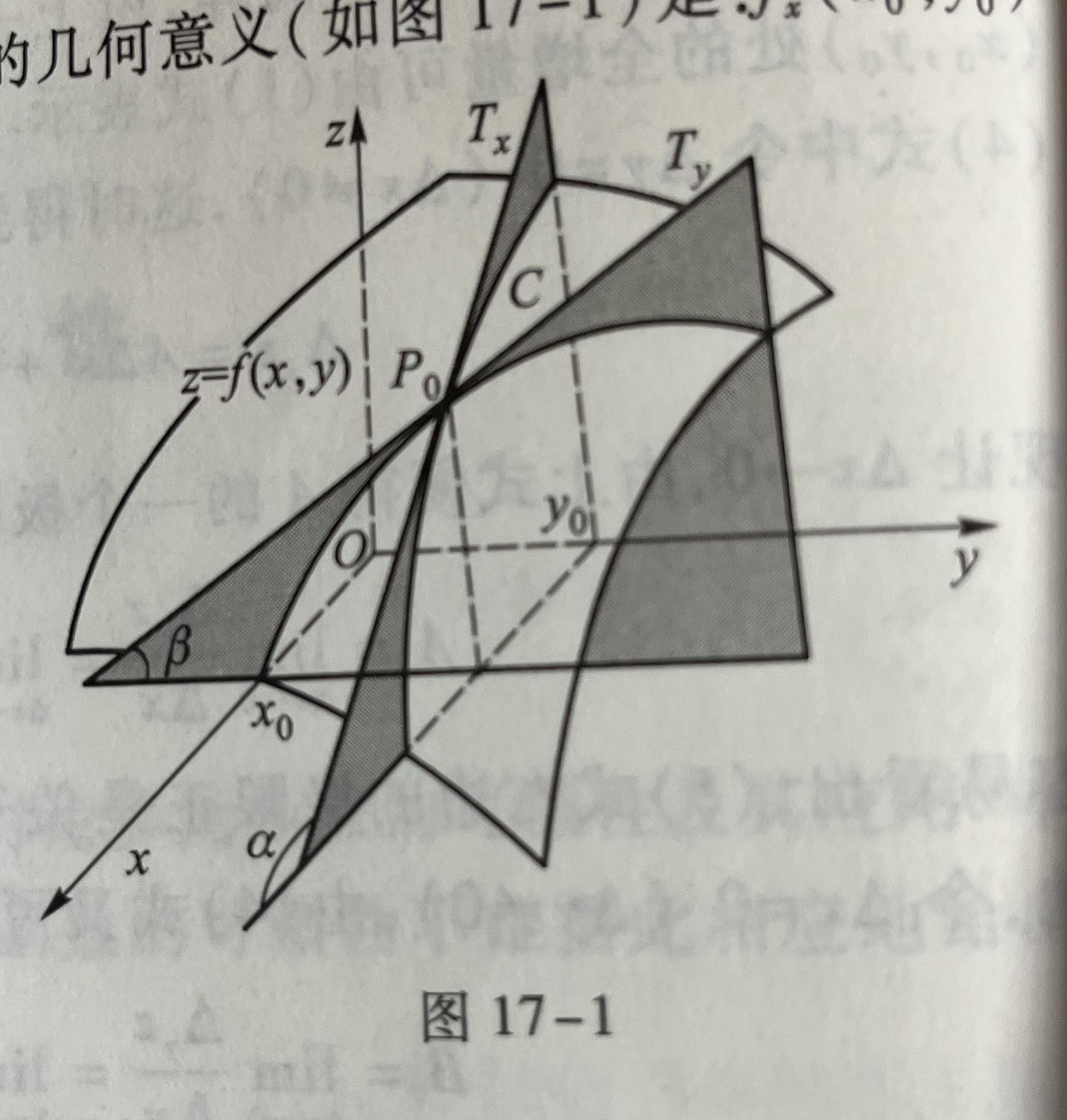
首先将其视为平面与曲面的交线,从而得到一条曲线,然后就可以看作平面上一元函数的切线了
可微的必要条件:
关于每个自变量的偏导数都存在,且等于可微定义中的 \(A\) \(B\)
可微的充分条件:
偏导数在邻域内存在,偏导数在该点连续
全微分:
\(A \Delta x + B \Delta y\)
|
proof:
把全增量拆成两个,其中每一个都是固定一个变量,考虑另一个变量的增量 再对它们分别用一元函数的拉格朗日中值定理写成微分的定义的形式 |
注意:
与一元函数的可导一定连续,连续不一定可导不同,二元函数可微并不一定能推出连续
例如反例:
它在 \((0,0)\) 处可微,但在 \((0,0)\) 处不连续
为什么这一结论与一元函数截然不同呢?
那是因为偏导数只能刻画二元函数在某一方向上的变化情况,而不能反应出二元函数的整体情况
|
定理:曲面 $z=f(x,y)在点 P 存在不平行于 z 轴的切平面 \Leftrightarrow f在点 P 处可微$
可类比平面存在不平行于 \(y\) 轴的切线的情况,详细证明待补充 |
习题
这个题目很好地说明了偏导数均存在时,仍然可能出现不可微的情况
考察可微:
因为如果可微,可以将 $\Delta f $表示为 \(A \Delta x + B \Delta y + o(\rho)\)
所以计算 $\Delta f - A \Delta x - B \Delta $ 比上 \(\rho\) 的极限,其中 \(A\)和\(B\) 为刚刚计算出的偏导数值
取 \(\Delta x = \Delta y\) 和 \(\Delta y = 0\) 可得知极限不存在,从而不可微
2.复合函数微分法
注意:用链式求导法则的前提必须是外层函数可微
3.方向导数与梯度
动机:在一些问题中要知道函数在某个特定方向上的变化率
若可微,则一定各个方向导数存在,而方向导数存在,不一定能推出可微
例2中的函数为什么不可微(存疑)
梯度:是一个向量,记作 \(grad f = (f_{x}(P_{0}),f_{y}(P_{0}),f_{z}(P_{0}))\)
4.泰勒公式与极值问题
通过构造一些不常规的函数,即在 \((0,0)\) 处有单独表达式的函数,发现这些函数的混合偏导数与求导顺序
有关,于是寻求混合偏导数与求导顺序无关的条件
|
定理:若 $f_{xy}(x,y)$ 和 $f_{yx}(x,y)$ 在 $(x_{0},y_{0})$ 处都连续,则偏导数换次序后仍然相等
proof: 回归导数的本质 -> 与极限有着密切的关系 因此从混合偏导数的极限形式出发 令 \(F(\Delta x,\Delta y)=f(x_{0} + \Delta x,y_{0} + \Delta y)-f(x_{0} + \Delta x,y_{0})-f(x_{0},y_{0} + \Delta y)+f(x_{0},y_{0})\) 为了方便对某个变量单独考虑,再令 \(\phi (x)=f(x,y_{0}+\Delta y)-f(x,y_{0})\) 所以可将 \(F(\Delta x,\Delta y)\) 表示成 \(\phi (x_{0}+\Delta x)-\phi (x_{0})\) 然后对函数 \(\phi\) 用一元函数的中值定理,即可将变量 \(x\) 固定,而 \(y\) 变化 再对以 \(y\) 为自变量的函数 \(f_{x}\) 用一元函数的中值定理,即可将上式化为 \(f_{xy}(x_{0}+\theta_{1}\Delta x,y_{0}+\theta_{2}\Delta y)\Delta x\Delta y\) 改变构造顺序,即可发现得到的两个结果相等 |
中值定理:
二元函数的中值定理与一元的类似,但是要先定义凸开域
|
定理:任意两点 $P(a,b),Q(a+h,b+k) \in D ,\exits \theta$使得
\(f(a+h,b+k)-f(a,b)=f_{x}(a+\theta h,b+\theta k)h+f_{y}(a+\theta h,b+\theta k)k\) proof: 令 \(\Phi(t)=f(a+th,b+tk)\) 则 \(\Phi(t)\) 是定义在 \([0,1]\) 上的一元函数(这里由凸开域来保证) 所以由一元函数的中值定理,\(\exits \theta \in [0,1]\),使得 \(\Phi(1)-\Phi(0)= \Phi ^\prime(\theta)\) 即得到原式 |
矩形区域为什么不能直接成立中值定理?(存疑)
泰勒定理:证明的时候思路一样,也是先构造一个一元函数,然后按照一元的泰勒展开,求得各阶导数
形式:\(f(x_{0}+h,y_{0}+k)=f(x_{0},y_{0})+(h\frac{\delta}{\delta x}+k\frac{\delta}{\delta y})f(x_{0},y_{0})+(\frac{1}{2!}(h\frac{\delta}{\delta x}+k\frac{\delta}{\delta y}))^{2}f(x_{0},y_{0})+...+\frac{1}{(n+1)!}((h\frac{\delta}{\delta x}+k\frac{\delta}{\delta y})^{n+1})f(x_{0}+\theta h,y_{0}+\theta k)\)
极值的必要条件:若函取得极值,并且在该点各个偏导数存在的话,则它们都等于 \(0\)
思考:如果在一个点取得极值,一些偏导数存在,一些偏导数不存在,那不存在的是否等于 \(0\) 呢?
|
定理(极值的充分条件): \(f\) 在 \(P_{0}\) 的某邻域上具有二阶连续偏导数,且 \(P_{0}\) 是 \(f\) 的稳定点,当 \(H_{f}(P_{0})\) 是正定矩阵时, \(f\) 在 \(P_{0}\) 取极大值,是不定矩阵时取极小值 proof: 利用泰勒公式,一阶导均等于 \(0\),我们考虑展开到二阶 \(f(x,y)-f(x_{0},y_{0})=\frac{1}{2}(\Delta x,\Delta y)H_{f}(P_{0})(\Delta x,\Delta y)^{T}+o(\Delta x^{2}+\Delta y^{2})\) 而\(H_{f}(P_{0})\)正定,所以对于任何\((\Delta x,\Delta y)\neq (0,0)\)都有二次型 \(Q(\Delta x,\Delta y)>0\) 所以存在一个与\(\Delta x\),\(\Delta y\)无关的正数\(q\)使得 \(Q(\Delta x,\Delta y) \geq 2q(\Delta x^{2},\Delta y^{2})\) 所以\(f(x,y)-f(x_{0},y_{0} \geq q(\Delta x^{2}+\Delta y^{2})+o(\Delta x^{2}+\Delta y^{2})\) \(=(\Delta x^{2}+\Delta y^{2})(q+o(1)) \geq 0\) 所以\(f\)在点\((x_{0},y_{0})\)取得极小值 同理,当\(H_{f}(P_{0})\)负定时,\(f\)在\((x_{0},y_{0})\)处取得极大值 最后来证明当\(H_{f}(P_{0})\)不定时,\(f\)在\(P_{0}\)处不取得极值 先假设\(f\)在该点处取得极值,然后考虑过\(P_{0}\)的直线\(x=x_{0}+t\delta x,y=y_{0}+t\delta y\),将其 视作关于\(t\)的一元函数,它在\(t=0\)处取得极值,所以可得到\(H_{f}(P_{0})\)是半正定或者半负定的,矛盾 |
由这个证明,又可以得到如下有用、好用的结论
- 一阶顺序主子式大于\(0\),二阶顺序主子式大于\(0\),取得极小值(正定)
- 一阶顺序主子式小于\(0\),二阶顺序主子式大于\(0\),取得极大值(负定)
- 二阶顺序主子式小于\(0\),不取极值(负定)
- (不完全理解,待补)
(存疑:极值充分条件中的正定、负定可以换成半正定、半负定吗)
习题
17.4
6.令\(x_{0}=0,y_{0}=0,h=\frac{\pi}{3},k=\frac{\pi}{6}\)
3.隐函数定理及其应用
1.隐函数
动机:对于显函数,讨论其连续性、可微性是容易的,而对于隐函数则需要另寻他路
隐函数定理的几何意义
隐函数是一个局部的概念,我们讨论隐函数时只能说在某个\(P_{0}\)附近确定了一个隐函数
你是否会有疑问,为什么隐函数不同于我们之前所学的函数,而只是一个局部概念呢?
我们先拿最简单的单位圆来举例,它的方程是\(x^{2}+y^{2}=1\),现在你位于圆上的任意一点,你可以向任意方向迈出一小步
我们先不妨令\(x^{2}+y^{2}=1=s\),记你沿\(x\)方向的移动为\(dx\),沿\(y\)方向的移动为\(dy\),沿\(s\)方向的移动为\(ds\)(沿\(s\)方向不太直观,可以自行脑补一下)
进行移动后,以单位圆为参照,你的状态无非就以下两种:
1.仍然位于圆上
2.跑到了圆外
这两种情况有什么本质区别呢?
在圆上,则坐标平方之和仍然为\(1\),所以\(ds=0\)
跑到圆外,则\(ds \neq 0\)
对于\(x^{2}+y{2}=1\),我们对其两边进行求导,得到
\(2xdx+2ydy=0\)
这个等式便是保证你仍然位于圆上的条件,写成另一种形式,也就是
\(\frac{dy}{dx}=\frac{-x}{y}\)
显然,当\(y=0\)时,上式是没有意义的,也就是当\(y=0\)时,我们无法找到一种方案,保证你在圆上
所以当\(y=0\)时,无法确定唯一的隐函数
所以从这个角度理解,隐函数就是对于在曲线上的一点,寻找一种仍能保证你微小移动后仍在曲线上的可行方案,
且这个方案应当是唯一的,不然也违背了“函数”的初衷
|
定理(隐函数存在唯一定理):
\(F(x,y)\)满足条件:
纸面上的)
则
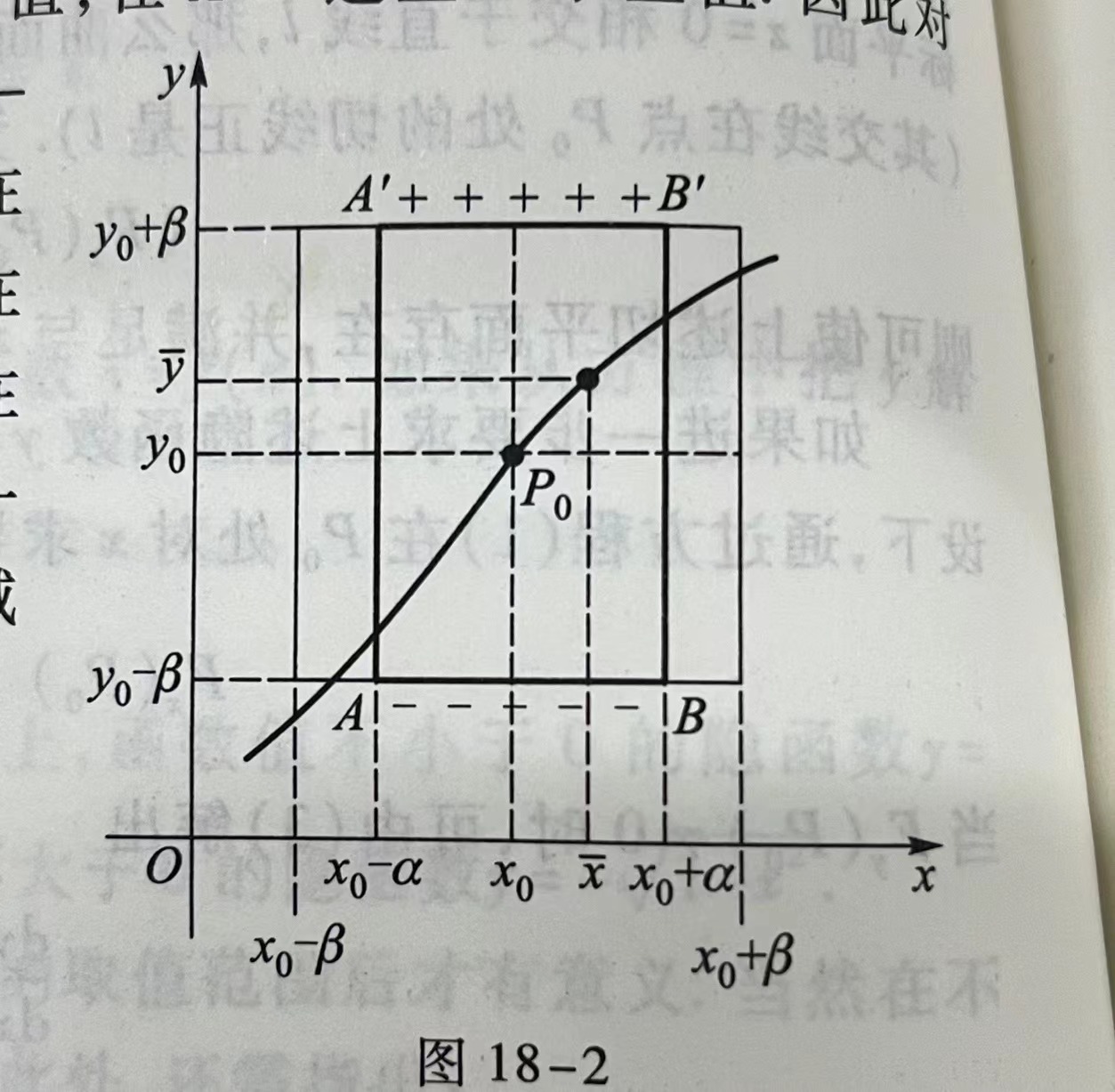
且有\(F(x,f(x))\equiv 0,f(x_{0})=y_{0}\) 2.\(f(x)\)在\((x_{0}-\alpha,x_{0}+\alpha)\)上连续 proof: 假设\(F_{y}(x_{0},y_{0})>0\),则由连续函数的局部保号性 在\(P_{0}\)的某一方形邻域\([x_{0}-\beta,x_{0}+\beta] \times [y_{0}-\beta,y_{0}+\beta]\)上,其上的每一点都有\(F_{y}(x,y)>0\) 用图形表示,就是如下的矩形\(ABB'A'\)
在\(AB\)上\(F\)取负值,在\(A'B'\)上\(F\)取正值,而当我们固定下来每一个 \(x_{s}\) 后,从垂直于\(x\)轴的方向来看,它在 \([y_{0}-\beta,y_{0}+\beta]\)上连续且严格增,所以由介值定理必有取\(0\)之时(且是唯一的),然后又有\(x\)的任意性即可证得 |
|
隐函数可微性定理:\(F(x,y)\)满足隐函数存在唯一性定理中的四个条件,又在\(D\)上存在连续的偏导数\(F_{x}(x,y)\),则\(f(x)\)在定义域\((x_{0}-\alpha,x_{0}+\alpha)\)上有连续导数,并且 \(f^{\prime}(x)=\frac{-F_{x}}{f_{y}}\) 这一定理仍旧可以用单位圆\(x^{2}+y^{2}=1\)来理解,对于几何意义中的求导,我们得到 \(\frac{dy}{dx}=\frac{-x}{y}\), 如果直接解出它的隐函数\(y=\sqrt(1-x^{2})\),对它进行以\(x\)为自变量的求导,得到的结果相同 |
隐函数可微性定理的严格证明:
设\(x\)和\(x+\delta x\)都属于\((x_{0}-\alpha,x_{0}+\alpha)\),它们对应的函数值都含于\((y_{0}-\beta,y_{0}+\beta)\)
所以,\(F(x,y)=0,F(x+\delta x,y+\delta y)=0\)
然后由二元函数的中值定理,
\(0=F(x+\delta x,y+\delta y)-f(x,y)=F_{x}(x+\theta \delta x,y+\theta \delta y)\delta x+F_{y}(x+\theta \delta x,y+\theta \delta y)\delta y\)
后续证明有待理解(待补)
类似地,我们还可以把这一定理推广到\(n\)元
2.隐函数组
3.几何应用
4.条件极值
在正常求极值的条件下加入了某些等式的限制(实际应用中显得尤为重要)
和探讨隐函数一样,直接进行消元往往是无法实现的,所以需要寻求一种不依赖于消元的方法
从简单的二元情况入手,求函数\(f(x,y)\)的极值,其中\((x,y)\)受条件\(\phi(x,y)=0\)的限制
和隐函数相似的,设\(x_{0}\)为\(z=h(x)=f(x,g(x))\)的极值点,在\(x_{0}\)处求导,得到
\(h^{\prime}(x_{0})=f_{x}(x_{0},y_{0})+f_{y}(x_{0},y_{0})g^{\prime}{x_{0}}=0\)
而又由隐函数的条件,成立
\(g^{\prime}(x_{0})=\frac{\phi_{x}(x_{0},y_{0})}{\phi_{y}(x_{0},y_{0})}\)
两式联立,可得
\(f_{x}(P_{0})\phi_{y}(P_{0})-f_{y}(P_{0})\phi_{x}(P_{0})=0\)
(待补)
得到拉格朗日乘数法
更多元的拉格朗日乘数法(需参看第23章)
4.含参量积分
1.含参量正常积分
设\(f(x,y)\)是在矩形区域\([a,b]\times[c,d]\)上的二元函数,固定\(x\)后,\(f(x,y)\)便变为定义在\([c,d]\)上的关于\(y\)的一元函数
这时对\(f(x,y)\)进行积分,得到的值必与刚刚固定的那个\(x\)有关,因此对于整个\([c,d]\)进行积分,得到的积分值便是\(x\)在\([a,b]\)上取值的函数
所以
\(\phi(x)=\int_{c}^{d}f(x,y)dy\)
连续性:\(f(x,y)\)在\([a,b]\times[c,d]\)上连续,则\(\phi(x)=\int_{c}^{d}f(x,y)dy\)在\([a,b]\)上连续
proof:
设\(x\)和\(x+\Delta x\)属于\([a,b]\),所以
\(\phi(x+\Delta x)-\phi(x)=\int_{c}^{d}[f(x+\Delta x,y)-f(x,y)]dy\)
因为\(f(x,y)\)在闭区域连续,所以在闭区域上一致连续,所以\(\forall \epsilon > 0\),\(\exists \delta\)
当\(|x_{1}-x_{2}|<\delta,|y_{1}-y_{2}|<\delta\)时,就有
\(|f(x_{1},y_{1})-f(x_{2},y_{2})|<\epsilon\)
所以\(|\phi(x+\Delta x)-\phi(x)|\leq \int_{c}^{d}|f(x+\Delta x,y)-f(x,y)|dy<\int_{c}^{d}\epsilon dx=\epsilon (d-c)\)
所以\(\phi(x)\)在\([a,b]\)上连续
同理\(\Phi(y)\)在\([c,d]\)上连续
这个定理也正好说明,积分和取极限可以交换顺序
连续性2:\(f(x,y)\)在区域\(G={(x,y)|c(x)\leq y \leq d(x),a \leq x \leq b}\)上连续,其中\(c(x)\)和\(d(x)\)为\([a,b]\)上的连续函数,则函数\(F(x)=\int_{c(x)}^{d(x)}f(x,y)dy\)在\([a,b]\)上连续
proof:
利用换元积分法,令\(y=c(x)+t(d(x)-c(x))\),当\(y\)在\([c(x),d(x)]\)上取值,\(t\)在\([0,1]\)上取值,
\(dy=(d(x)-c(x))dt\)
所以\(F(x)=\int_{0}^{1}f(x,c(x)+t(d(x)-c(x)))(d(x)-c(x))dt\),而被积函数在\([a,b]\times [0,1]\)上连续
所以确定下来的函数\(F(x)\)在\([a,b]\)上连续
可微性:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号