2-13

差分

定义： 设变量y依赖于自变量t ,当t变到t + 1时,因变量y = y(t)的改变量Dy(t)= y(t+1) - y(t)称为函数y(t)在点t处步长为1的(一阶)差分，记作Dy1= yt+1- yt，简称为函数y(t)的(一阶)差分,并称D为差分算子。 差分具有类似于微分的运算性质。

向前差分

x_k=x₀+kh  (k=0,1,2,.......,n)-

Δf(xk) =  Δf(xk+1) - Δf(x k) 

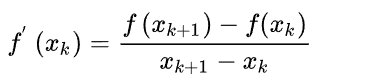
向后差分

Δf(xk) =  Δf(xk) - Δf(x k-1)

 

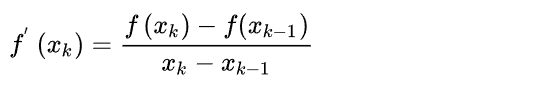
中心差分

Δf(xk) =1/2*（ Δf(xk+1) - Δf(x k-1) ）

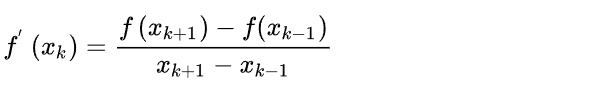
函数在每个小区间上的增量y(k+1)-yk为f(x)的一阶前向差分。在微积分学中的有限差分，前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当是多项式时，前向差分为Delta算子，一种线性算子。前向差分会将多项式阶数降低1。

 

C++中应用：

void adjdif(int a[], int b[],int n)

{

  for(int i=1; i<=n;i++)

      b[i]=a[i]-a[i-1];

}

 

数组 ：  2  3  5  7  11  13  17  19

差分 ：  2  1  2  2  4  2  4  2

可以在第一个元素上加常数c，即可改变数组中每个元素；同理，区间L至R加c :

void Insert(int b[],int L,int R,int c)

{

  b[l]+=c;

  b[r+1]-=c;

}

 

二维数组：

void Insert(int x1, int x2, int y1, int y2, int c)

{//点(x1,y1) 在 (x2,y2)的左上方(或重合)

  b[x1][y1]+=c;

  b[x2+1][y2]-=c;

  b[x2][y2+1]-=c;

  b[x2][y2]+=c;

}

 

例：

第一行有两个整数n，p，代表学生数与增加分数的次数。

第二行有n个数，a1~an，代表各个学生的初始成绩。

接下来p行，每行有三个数，x，y，z，代表给第x个到第y个学生每人增加z分。

输出仅一行，代表更改分数后，全班的最低分。

#include <iostream>

using namespace std;

int main()

{

    std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

    int n,p;

    cin>>n>>p;

    int array[n+1];

    int array cf[n+1];

    for(int i=1; i<=n; i++) cin>>array[i];

    while(p--)

    {

        int x,y,z;

        cin>>x>>y>>z;

        cf[x]+=z;

        cf[y+1]-=z;

    }

    int ans=1e9,sum=0;

    for(int i=1;i<=n;i++)

    {

        array[i]=array[i]+sum+cf[i];

        sum+=cf[i];

        ans= min(ans,array[i]);

    }

    cout<<ans<<endl;

    return 0;

}

 

 

#include <iostream>

#include <algorithm>

using namespace std;

int main()

{

    std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

    int n,q;

    cin>>n>>q;

    int t[n],array[n];

    array[0]=0;

    for(int i = 0; i<n; i++)

        cin>>t[i];

    for(int i=n-1; i>=1; i--)

        t[i]-=t[i-1];

    sort(t+1,t+n);

    for(int i = 1; i<n; i++)

        array[i]=t[i]+array[i-1];

    while(q--)

    {

        int k,p;

        cin>>k>>p;

        int abs=lower_bound(t+1,t+n,k)-t;

        int ans=array[n-1]-array[abs-1]-(n-1-abs+1)*k;

        if(ans>=p) cout<<"Yes"<<endl;

        else cout<<"No"<<endl;;

    }

    return 0;

}

 

前缀和：

一维数组前缀和：  y_n = y_n-1 + x_n  ;

for(int i=0;i<n;i++)

{

    if(i==0) y[i]=x[i];

    else y[i]=y[i-1]+x[i];

}

 

二维前缀和：ax,y = ax-1,y + ax,y-1  - ax-1,y-1 + ax,y  ;

for(int y=0;y<n;y++)

{

    for(int x=0;x<m;x++)

    {

        if(x==0 && y==0) 

            b[y][x]=a[y][x];//左上角的值

        else if(x==0) 

            b[y][x]=b[y-1][x]+a[y][x];//第一列

        else if(y==0) 

            b[y][x]=b[y][x-1]+a[y][x];//第一行

        else 

            b[y][x]=b[y-1][x]+b[y][x-1]-b[y-1][x-1]+a[y][x];

    }

}

前缀和是一种预处理，用于降低查询时的时间复杂度。

给定 n   个整数，然后进行 m  次询问，每次询问求一个区间内值的和。

如果用暴力写法，那每次询问都需要从区间左端点循环到区间右端点求和，时间复杂度较大。这种时候就可以预先求出该数组的一维前缀和。

则 ans = y[R] - y[L - 1] ,其中， L 和 R 是给定区间，每次询问可直接输出答案，复杂度从 O（n*m）降到了O（n+m）。