傅立叶变换与使用

在看三体的时候有一种叫做维度打击的事情，傅立叶变换也就是属于此类事件吧

摘自百度百科，手动整理添加

傅里叶变换的定义

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合

傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成频率谱——显示与频率对应的幅值大小）。

 

傅里叶变换的原理

第一幅图是一个余弦波 cos（x）

第二幅图是 2 个余弦波的叠加 cos (x) +a.cos (3x)

第三幅图是 4 个余弦波的叠加

第四幅图是 10 个余弦波的叠加

随着正弦波数量逐渐的增长，他们最终会叠加成一个标准的矩形。

在不同的方向观察会得出不同的结论，在时域上是那个样子，在频域上确实另外的一个样子如下图

 

不仅仅是矩形，你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点，但是一旦接受了这样的设定，游戏就开始有意思起来了。

是上图的正弦波累加成矩形波，我们换一个角度来看看：

这就是矩形波在频域的样子，是不是完全认不出来了？教科书一般就给到这里然后留给了读者无穷的遐想，以及无穷的吐槽，其实教科书只要补一张图就足够了：频域图像，也就是俗称的频谱。

可以发现，在频谱中，偶数项的振幅都是0，也就对应了图中的彩色直线。振幅为 0 的正弦波。

所以我们可以很简单的分析出这个波形的性质是什么，不就是10 个余弦波的叠加么，但如果你从时域上分析是很难得出这个结论的。

 

信号处理上使用傅里叶变换的好处

傅里叶变换的主要实践好处是工程分析，可以从另外一个角度去观察你采集到的信号。

而且从这个角度分析得出结果的速度比原来的角度快很多，傅里叶变换提供了很多的变换手法在很多场景上有使用。

但对于我们工科的人来说往往只要懂得拿来用就可以啦，这个看上去像不像是维度打击呀 哈哈

 

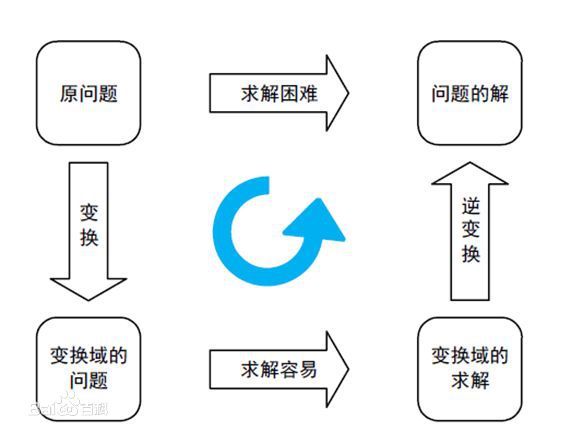
傅立叶变换的实际使用

傅里叶变换在很多场景都有使用，对于我们来说，主要是要懂得怎么在工具上使用，具体看是什么领域需要吧

我所知道的工具有对于音频分析使用 Audacity  

以及数学以及图像信号处理上使用 MATLAB

还有就是我们的python上有很多对于的库也能进行分析处理