组合数学

基本定义在此不再过多阐述，介绍一下基本符号：

\(\dbinom{n}{m}=C_n^m\)，含义为 \(n\) 选 \(m\) 的组合方案数。

\(A_n^m\)，含义为 \(n\) 选 \(m\) 的排列方案数。

求组合数方式

一般采用预处理阶乘与逆元做到线性求组合数。

如果求 \(\dbinom{n}{m}\) 时 \(n\) 极大而 \(m\) 较小，此时无法预处理 \(n\) 的阶乘和逆元，可以采用下降幂运算，即预处理 \(m\) 的阶乘和逆元，将原式写为：

\[\dbinom{n}{m}=\prod_{i=n-m+1}^n \times \dfrac{1}{m!} \]

这样就可以用较快的时间来求出组合数。

错位排列数

• 使用容斥：

\[\begin{aligned} F_n&=\sum_{i=0}^n \dbinom{n}{i} \times (n-i)! \times (-1)^i \\&=n! \times \sum_{i=0}^n \dfrac{1}{i!} \times (-1)^i \end{aligned} \]

乘号后面进行预处理即可。

• 使用递推：设填后的序列第 \(i\) 为 \(p_i\)，将 \(i\) 向 \(p_i\) 连边。考察 \(1\) 所在的环，设其长度为 \(i\)。去掉 \(1\) 所在的环，剩下的数的方案数为 \(F_{n-i}\)。所以枚举 \(i\)，同时计算长度为 \(i\) 环上的数方案数，有：

\[\begin{aligned} F_n&=\sum_{i=2}^n F_{n-i} \times \dfrac{(n-1)!}{(n-i)!} \\&=(n-1)! \times \sum_{i=0}^{n-2} \dfrac{F_i}{i!} \end{aligned} \]

在计算 \(F_n\) 的同时，维护乘号后面的式子。

• 依然是递推：对上文的递推进行简化，仍然考察 \(1\) 所在的环，将 \(1\) 去掉同时将环上和 \(1\) 相邻的两个点连上，等价于对后面 \(n-1\) 个数做错排。注意当 \(1\) 所在环只有 \(1\) 和另外一个点的时候，由于点不能指向自己，此时相当于对剩下 \(n-2\) 个数做错排。

还有一种理解方式，考虑现在已经有一个合法的错排图，要向里面加入一个点，则可以在任意一条边加入该点，但这样只考虑到了新加入的点所在环长度大于 \(2\) 的情况，所以还需考虑在其中取出一个点，与新加的点互相连边，剩下的点形成一张错排图。

综上有：\(F_{n}=(n-1)(F_{n-1}+F_{n-2})\)。

「KDOI-02」一个仇的复

观察数据范围，猜测最终时间复杂度为 \(O(k^2)\)。

发现方格宽度为 \(2\)，只能容下大小为 \(1,2\) 的方块竖着放，不妨将 \(1\) 看作横着放，所以只需要考虑有多少个 \(2\) 竖着放即可，设个数为 \(i\)，对 \(i\) 进行枚举，时间消耗为 \(O(k)\)，其中 \(i \in [0,k]\)。

现在问题化为两个子问题，一个为选竖着的 \(2\) 的方案数，一个为放完竖着的 \(2\) 后整个网格横着放的方案数。不妨先考虑第二个子问题。

先思考没有竖着的 \(2\) 的方案数。将其展开为 \(1 \times 2n\) 的平面，考虑插板，由于已经有两个基本块，所以只需要再插 \(k-2\) 个板，而在 \(n\) 与 \(n+1\) 之间无法插板，所以可供插板空隙为 \(2n-2\)，故方案数为 \(\tbinom{2n-2}{k-2}\)。

现在考虑有竖着的 \(2\) 情况，由于枚举了竖着的 \(2\) 的数量，设其为 \(i\)。因为该数量固定，所以影响空隙个数的只有形成的连通块个数，设其为 \(j\)，则空隙个数即为 \(2(n-i)-2j\)。同理，可供插的板也只与连通块个数有关，为 \(k-i-2j\)。故最终方案数为 \(\tbinom{2(n-i)-2j}{k-i-2j}\)。故需要枚举形成连通块数量，时间消耗为 \(O(k)\)，其中，\(j \in [1,i+1]\)。

接着考虑第一个子问题。由于需要分成 \(j\) 个连通块，所以用来分隔网格的竖着的 \(2\) 的连通块个数即为 \(j-1\)。但是如果竖着的 \(2\) 放在了开头或者末尾是不会影响网格连通块个数的，所以 \(2\) 连通块个数还可以为 \(j,j+1\)。对这个问题做插板，发现可以插 \(j+1\) 个板，而可供插板的空隙为 \(i\) 个的开头结尾和中间共计 \(i+1\) 个位置。所以该问题方案数为 \(\tbinom{i+1}{j}\)。

最后考虑放着这些连通块到网格的方案数，相当于将剩下的 \(2 \times (n-i)\) 个格子分为 \(j\) 块，仍然用插板法，得知方案数为 \(\tbinom{n-i-1}{j-1}\)。

发现有一种情况没有考虑，即 \(n=k\) 时选 \(k\) 个竖着的 \(2\) 的方案，这种情况无法刻画，因为没有形成连通块，最后特判加上即可。

最终答案为：

\[\begin{aligned} \\& \sum_{i=0}^k \sum_{j=1}^{i+1} \tbinom{2n-2i-2j}{k-i-2j} \times \tbinom{i+1}{j} \times \tbinom{n-i-1}{j-1} + [n=k]\\&= \sum_{i=0}^k \sum_{j=0}^{i} \tbinom{2n-2i-2j-2}{k-i-2j-2} \times \tbinom{i+1}{j+1} \times \tbinom{n-i-1}{j} +[n=k]\end{aligned} \]

可能空间开不下，但是发现可以预处理后两个组合数的阶乘和逆元，对前一个组合数只预处理阶乘，求的时候现求逆元即可（或者都开成 \(int\)，强转 \(long long\)）。

广义组合数

• 当 \(n \ge m \ge 0\) 时，\(\dbinom{n}{m}=\dfrac{n!}{(n-m)!m!}\)

• 当 \(m \ge 0 \land m \ge n\) 时，\(\dbinom{n}{m}=\dfrac{\prod_{i=n-m+1}^n i}{m!}\)

• 由二式得，当 \(m \ge n \ge 0\) 时，有：

\[\begin{aligned} \dbinom{-n}{m}&=\dfrac{\prod_{i=-n-m+1}^{-n} i}{m!}\\&=\dfrac{(n+m-1)!}{(n-1)!m!} \times (-1)^m\\&=(-1)^m \times \dbinom{n+m-1}{m} \end{aligned} \]

[集训队互测 2012] calc

首先可以做一个简单的 dp，\(dp_{i,j}\) 表示考虑 \([1,i]\) 中的数，选了 \(j\) 个数在序列中的权值积，最后 \(dp_{k,n} \times n!\) 即为答案。

观察 dp 转移：\(dp_{i,j} = dp_{i-1,j} + dp_{i-1,j-1} \times i\)，发现转移系数和 \(i\) 有关，故矩阵快速幂中的转移矩阵不固定，没有前途。

本题生成函数对于笔者来说太过困难，所以在此只讨论使用拉插解题。

发现 dp 转移非常简洁，所以猜测对于固定的 \(j\)，\(dp_{i,j}\) 在一个多项式上。设 \(g(f_x)\) 表示 \(f_x\) 的多项式次数，则显然有，\(g(f_x-f_{x-1})=g(f_x)-1\)。观察 dp 转移式子，有：

\[\begin{aligned} &dp_{i,j}=dp_{i-1,j}+dp_{i-1,j-1} \times i \\&dp_{i,j}-dp_{i-1,j}=dp_{i-1,j-1} \\&g(f_j)-1=g(f_{j-1})+1 \end{aligned}\]

又因为 \(g(f_0)=0\) 次，所以 \(g(f_j)=2j\)。因此只需要做 \(2n+1\) 次 dp，然后拉插即可。

[JLOI2015] 骗我呢

发现值域为 \([0,m]\)，则一行只有一个位置会 \(+2\)，可以做出来简单 dp，优化过后变为 \(dp_{i,j}=dp_{i,j-1}+dp_{i-1,j+1}\)。

代数推导一点不会，组合意义天崩地裂。

发现式子很简洁，想用上一题的方法看看多项式，发现次数为 \(n\)，那肯定没救的。所以考虑组合意义，将其放在网格图上，考虑将 dp 值变为到达 \((i,j)\) 的路径条数，dp 转移看为一条边。发现转移中有斜着的边，不好处理，所以将其平移。发现行末仍然有一条斜边，将其扩展为先向右再向下，于是得到一张网格图。由于将每一行行末扩展了，所以每一行长度为 \(m+1\)，则问题变为在网格图上，从原点出发，到达 \((n+m+1,n)\) 的方案数，网格形状如下：

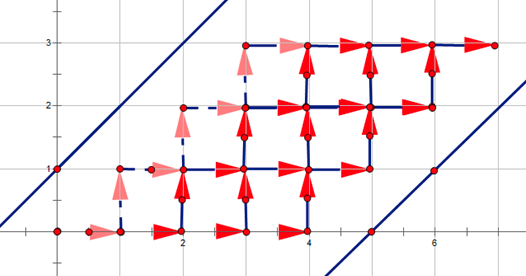
将网格形状转化为限制，变为不接触两条直线的方案数。称直线 \(A\) 为上方直线，直线 \(B\) 为下方直线，点 \(P\) 为 \((n+m+1,n)\)。考虑反射容斥，即将总方案数即从原点到 \(P\) 的路径数，减去碰到任意一条直线且可能越过直线的方案数，将碰到的直线依次写为一个序列，相邻相同的直线进行缩点，最后会得到 \(\cdots ABAB\) 或 \(\cdots BABA\)，将不合法方案分为末尾为 \(A\) 的方案和末尾为 \(B\) 的方案。发现将 \(P\) 沿直线 \(A\) 对称得到 \(P'\) 后，每一条从原点到达 \(P'\) 的路径都可以通过从第一次接触 \(A\) 开始对称，最终到达 \(P\)；同理，每一条从原点到达 \(P\) 且接触了 \(A\) 的路径都可以从第一次接触 \(A\) 开始对称，最后到达 \(P'\)，所以形成了双射。考虑这类方案对应接触序列是怎样的。考虑到达 \(P\) 且接触 \(A\) 的路径中从最后一次接触 \(A\) 到 \(P\) 的路径，由于为最后一次接触 \(A\)，所以不会再碰到 \(A\)，只有可能碰到 \(B\)。所以这类路径个数对应序列结尾为 \(A\) 或 \(AB\) 的序列个数；同理，若将 \(P\) 沿 \(B\) 反转，可以得到序列结尾为 \(B\) 或 \(BA\) 的序列个数。发现总共多减去结尾为 \(AB\) 和 \(BA\) 的序列个数。考虑将 \(P'\) 再次沿 \(B\) 对折，仍然考虑从原点到 \(P''\) 的路径中最后一次接触 \(B\) 来看，后面一定会接触 \(A\)，然后可能在去往 \(P\) 的路径上再次接触 \(B\)，所以路径末尾为 \(BA\) 或 \(BAB\)。

所以有一个简单的容斥，发现 \(P,P',P'' \cdots\) 形成的直线斜率为 \(-1\)，每两次对称一定会向 \(x,y\) 轴移动，所以至多移动线性次，所以时间复杂度为线性。

第一类斯特林数

\(s(n,k)\) 表示 \(n\) 个数，分为 \(k\) 个环（即 \(1,2,3,4\) 与 \(4,1,2,3\) 算一种方案）的方案数，记作 \(\displaystyle {n \brack m}\)。

有递推式：\(s(n,k)=s(n-1,k-1)+s(n-1,k) \times (n-1)\)。代表新加入的点是新增一个环还是插入到原有的环中共 \((n-1)\) 个位置中。

有性质：

• \(s(n,1)=(n-1)!\)，易证。

• \(s(n,2)=(n-1)! \times \sum_{i=1}^{n-1} \dfrac{1}{i}\)，证明考虑数学归纳法。

• \(\sum_{k=1}^n s(n,k)=n!\)。考虑任意一个排列都可以通过 \(i \to a_i\) 连边来映射成唯一一个由若干个环组成的图；同理，环也可以映射成唯一一个排列。二者形成双射。

下降幂

有 \(x^{\underline i}=\dfrac{x!}{(x-i)!}\)。文章开头即为下降幂优化求组合数式子。

其与组合数相乘有着优雅的形式，如下：

\[\begin{aligned} \dbinom{n}{k} \times k^{\underline m} &= \dfrac{n!}{(n-k)!(k-m)!}\\&=\dfrac{(n-m)!}{(n-k)!(k-m)!} \times \dfrac{n!}{(n-m)!}\\&=\dbinom{n-m}{n-k} \times n^{\underline m} \end{aligned} \]

发现原本式子中两个乘数都含有 \(k\)，转化完后只有一个式子含有 \(k\)。

第二类斯特林数

\(S(n,k)\) 表示 \(n\) 个数，分为 \(k\) 组，每组无序，组与组之间没有区别的方案数，记作 \(\displaystyle {n \brace m}\)。

有递推式：\(S(n,k)=S(n-1,k-1)+S(n-1,k) \times k\)。代表新加入的点是新增一组还是加入原有的 \(k\) 组中。

第二类斯特林数可用于转化幂：\(x^n=\sum_{i=1}^n \displaystyle {n \brace i} x^{\underline{i}}\)，证明考虑数学归纳法：

\[\begin{aligned} x^n&=x \times x^{n-1}\\&=x \times \sum_{i=1}^{n-1} \displaystyle {n-1 \brace i} x^{\underline i}\\&=\sum_{i=1}^{n-1} \displaystyle {n-1 \brace i} x^{\underline i} (x-i) + \sum_{i=1}^{n-1} \displaystyle {n-1 \brace i} x^{\underline i} i\\&=\sum_{i=1}^{n-1} \displaystyle {n-1 \brace i} x^{\underline {i+1}} + \sum_{i=1}^n \displaystyle {n-1 \brace i}x^{\underline i} i\\&=\sum_{i=1}^n \displaystyle {n-1 \brace i-1} x^{\underline i} + \sum_{i=1}^n \displaystyle {n-1 \brace i} x^{\underline i} i\\&=\sum_{i=1}^n \displaystyle {n \brace i} x^{\underline i} \end{aligned} \]

[省选联考 2020 A 卷] 组合数问题

发现原式为 \(k\) 的次幂乘上关于 \(k\) 的组合数，因为 \(k\) 很大，不能枚举，这个形式有不是那么好看，所以使用下降幂来将其优化一下。将原多项式变为下降幂多项式，设 \(f(x)=\sum_{i=0}^m b_i k^{\underline i}\)，然后开始转化：

\[\begin{aligned} &\sum_{k=0}^n f(k) x^k \dbinom{n}{k}\\=&\sum_{k=0}^n\sum_{i=0}^m b_i k^{\underline i} x^k \dbinom{n}{k}\\=&\sum_{k=0}^n \sum_{i=0}^m b_i \dbinom{n-i}{k-i} n^{\underline i} x^k \\=& \sum_{i=0}^m b_i n^{\underline i} \sum_{k=0}^{n-i} \dbinom{n-i}{k} x^{k+i}\\=&\sum_{i=0}^m b_i n^{\underline i} x^i \sum_{k=0}^{n-1} \dbinom{n-i}{k} x^k\\=&\sum_{i=0}^m b_i n^{\underline i} x^i (x+1)^{n-i} \end{aligned} \]

则问题转化为求 \(b_i\)。

因为有 \(x^n=\sum_{i=0}^n \displaystyle {n \brace i} x^{\underline i}\)，所以将 \(f(x)\) 进行转化：

\[\begin{aligned} f(x)&=\sum_{i=0}^m a_i x^i\\&= \sum_{i=0}^m a_i \sum_{j=0}^i \displaystyle {i \brace j} x^{\underline j}\\&=\sum_{i=0}^m x^{\underline i} \sum_{j=i}^m a_j \displaystyle {j \brace i} \end{aligned} \]

可以递推预处理出所有第二类斯特林数，然后 \(O(m^2)\) 求出所有 \(b_i\)，最后 \(O(m^2)\) 求出答案。

总时间复杂度 \(O(m^2)\)。