图论连通分量

无向图连通分量

定义

在无向连通图中，若删去一个节点 \(x\) 及所有与 \(x\) 关联的边后，该图被分为两个不连通的子图，则节点 \(x\) 称为割点。

在无向连通图中，若删去一条边 \(e\) 后，该图被分为两个不连通的子图，则该边 \(e\) 称为割边或桥。

而在无向图中，其割边与割点即为其各个连通块的割边与割点。

在一张无向连通图中，若不存在割点，则称其为“点双连通图”；若不存在割边，则称其为“边双连通图”。

一张无向图中，极大的点双连通图称为“点双连通分量”；极大的边双连通图称为“边双连通分量”。点双连通分量简称点双，简记为 “v-DCC”；边双连通分量简称边双，简记为 “e-DCC”。二者统称双连通分量，简记 “DCC”。

在无向图上，任选一点按照深度优先遍历的顺序叫做 dfs 序，依照每个点在 dfs 序中第一次被访问到的时间顺序，依次给予 \(N\) 个节点 \(1\) 至 \(N\) 的整数标记，该标记叫做时间戳。

在无向连通图上，任选一个点进行深度优先遍历，每个点仅允许被访问一次，则所有访问到的边组成一棵树，该树称为无向连通图的搜索树。在无向图中，所有的连通块的搜索树组成的森林叫做该无向图的搜索森林。

无向图中的 Tarjan 算法

Tarjan 算法可以求出无向图中的割边与割点。

对于一张无向图，可以对每个连通块分开处理，对于每个连通块求出割边与割点，故下文仅考虑无向连通图。先考虑割点的求法。

割点

首先无向连通图的边可以分为两部分：

• 在该无向连通图的搜索树上的边，称为树边。
• 不在该无向连通图的搜索树上的边，称为非树边。

性质 \(1\)

非树边连接的两个节点一定形成祖先后代关系。

证明：假如两个节点 \(x,y\) 先遍历的为 \(x\)，则遍历到 \(x\) 的时候由于 \(y\) 还未被遍历，则一定会由 \(x\) 或其子树中的节点遍历到 \(y\)，从而 \(x\) 成为 \(y\) 的祖先。

性质 \(2\)

一棵子树中的 \(dfn\) 一定是一段连续的区间。

证明：由于子树内的节点在 dfs 序的情况下是连续的，故其 \(dfn\) 也是连续的。

若该图是一棵树，则除该树根之外，每个节点都一定是割点，证明显然。考虑什么时候根为割点，显然若根的儿子数量只有一个的时候，其不是割点；否则删去根之后，原树变为多个不连通的子树，即根为割点。

根据割点的定义，若一个点 \(x\) 的子树（下文简记为 \(T(x)\)）中有节点在不经过该点的情况下无法与整张图除该点子树外的点（下文简记为 \(T'(x)\)）连通，则该点为割点。

由于该点每个儿子的子树连通，所以只需要判断该点所有的儿子能否不通过 \(x\) 到达 \(T'(x)\) 即可。所以我们可以记录 \(dp_i\) 代表 \(i\) 点在只到达 \(T(i)\) 的情况下能达到的最小 \(dfn\)。

若存在 \(son_x\) 使得 \(dp_{son_x} \ge dfn_x\) 则说明该子树在不经过 \(x\) 的情况下只能到达自己本身，即该点为割点。由此可推出状态转移方程 \(dp_x=\min(\min_{son_x} dp_{son_x},\min_{e \in 非树边} dfn_{v})\)，若 \(dp_{son_x} \ge dfn_x\)，则 \(x\) 为割点。注意此时是只有对通过非树边到达的点的 \(dfn\) 取最小值，而每个节点的父亲与该节点的连边显然不是非树边，但由于更新父亲的 \(dfn\) 并不会影响判定，所以方便起见，只要是访问过的节点我们都对其的 \(dfn\) 取最小值，其他取 \(dp\) 值。

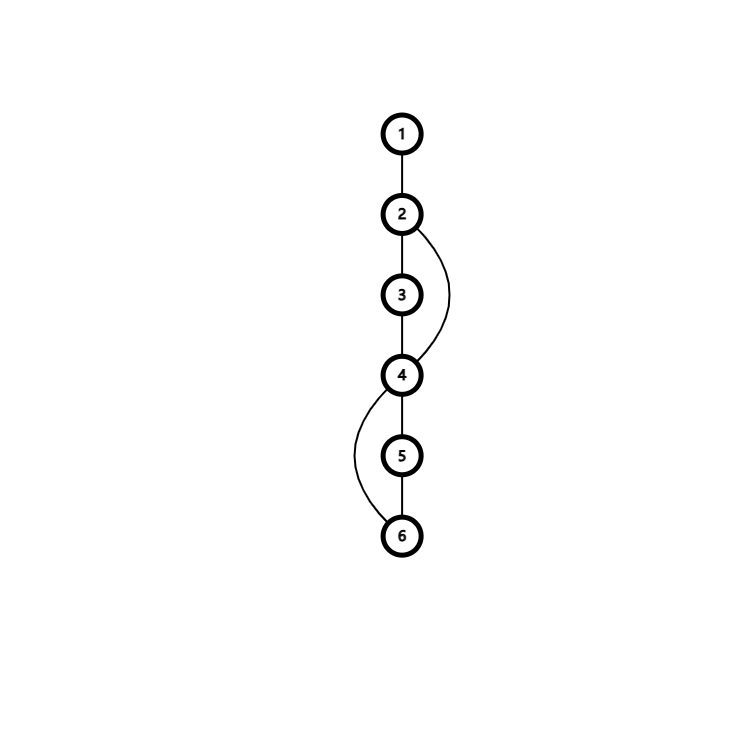
此时会引出一个问题：我们能否对访问过的节点的 \(dp\) 取最小值？首先对于父亲节点肯定不行，若父亲节点提前访问到了祖先节点，则 \(dp_{fa}=dfn_{fa_{fa}}\)，所以所有的儿子的 \(dp\) 也会变为 \(dfn_{fa_{fa}}\)，这相当于是经过了 \(T'(x)\) 后能到达的 \(dfn\) 最小值，不符合我们对 \(dp\) 数组的定义。那么改为对通过非树边到达的节点的 \(dp\) 取最小值呢？考虑与父亲节点有重边，变为上述情况。那如果除了父亲呢？考虑下图：

先来看一个性质。

性质 \(3\)

一个点可以属于多个点双，若多个点双共有一个点，那该点一定为割点。

证明：充分性：若一个割点连接两个连通块，则将该节点删去，两个连通块内部仍然连通，互相不连通，这保证了该割点属于两个点双，且两个点双无法合并为一个点双。

必要性：考虑若多个点双共用多个点，则删去其中任意一个共用的点，各个点双内部连通，外部可以通过其他共用的点连通，故原假设不成立。若多个点双给共用的不是割点，说明删去该点后，图仍然连通，说明连通性没有改变；同时，删去点双中的其他点，该点双显然连通，同时也不会对其他点双造成连通性的影响，所以这多个点连通图不是极大的，可以合并，所以其不是点双，原假设不成立。

回到上图，此时 \(dp_6=dp_3=dp_1=dfn_1=1\)，所以 \(dp_5=dp_6=1<dfn_4\)，故按照这样 \(4\) 号节点不能算为割点，但其肯定为割点，就其根本原因还是一个割点可以属于多个点双，如果按照 \(dp\) 更新的话，相当于将两个点双合并了。（建议看完如何求解割边再看后文）如果是割边或者求边双的话，由于一条点顶多属于一个边双，所以即使按照 \(dp\) 更新，也不会将其他的边双的 \(dp\) 更新到当前边双中，所以是可以的。

这就是 \(low\) 数组的含义，一般地，我们将 \(dp_x\) 初始化为 \(dfn_x\)，显然不会影响答案。

void dfs(int u){
    int son=0;
    dfn[u]=++dn,low[u]=dfn[u],vis[u]=true;
    for(int dao:g[u]){
	if(!vis[dao]){
	    dfs(dao);
	    if(low[dao]>=dfn[u]&&u!=rt) sum+=ans[u]?0:1,ans[u]=true;
	    low[u]=min(low[u],low[dao]);
	    son++;
        }
        else low[u]=min(low[u],dfn[dao]);
    }
    if(u==rt&&son>1) sum+=ans[u]?0:1,ans[u]=true;
}

割边

仿照割点的求法，发现割边的判定条件与割点有所不同，如下图：

会发现，在点 \(2\) 至点 \(6\) 中，割点为 \(2\) 与 \(4\)，但是并没有任何一个割边。而根据定义，发现假如现在判定的是 \((4,5)\) 这条边，那么判定的条件应该是 \(5\) 及以下的节点不通过 \((4,5)\) 这条边能到达的最高（即最小 \(dfn\)）点在 \(4\) 之下（不包括 \(4\)）。因为到达 \(4\) 之后其就不必借助 \((4,5)\) 这条边能与 \(T'(4)\) 连通。

由此可推出状态转移方程 \(dp_x=\min(\min_{son_x} dp_{son_x},\min_{e \in 非树边} dfn_{v})\)，若 \(dp_{son_x} > dfn_x\)，则 \((x,son_x)\) 为割边。注意，此时是必须为非树边，也就是说不能通过 \(dfn_{fa}\) 更新，但如果有重边那也就是非树边就能用 \(dfn_{fa}\) 更新。所以在 dfs 的时候可以传进去进来的边的编号，如果枚举到这条边的反向边，那就直接跳过即可。

dfn[u]=++dn,low[u]=dn;
for(int i=head[u];i;i=nxt[i]){
    int dao=ver[i];
    if(((i&1)&&v==i+1)||(!(i&1)&&v==i-1)) continue;
    if(!low[dao]){
	dfs(dao,i);
        if(low[dao]>dfn[u])
            mk[i]=true,mk[i&1?i+1:i-1]=true;
	low[u]=min(low[u],low[dao]);
    }else low[u]=min(low[u],dfn[dao]);
}

边双

对于边双的求解，我们有两种方法：

• 第一种，求出割边之后做一遍 dfs，割边将整张图分为若干个边双，此时，求解割边的时候就不必判断重边，只需判断是否是父亲节点即可。因为假如有重边，也只会标记那一条边为重边，然而 dfs 的时候会递归另外一条边，所以点双求解是正确的，但是如果输出割边那就是不正确的。
• 第二种，由于边双是搜索树上的一个连通块，且每个点仅属于一个边双，所以考虑用栈存储下来每个点，当搜索完一个节点的所有子树后，且当前节点是该边双的起点时，就可以一直出栈直至到该节点。

对于第二种，问题来到如何判断一个点 \(x\) 是否是该边双的起点。

分两种情况：

• 若 \(low_{son_x}<dfn_x\)，说明儿子可以不通过 \((x,son_x)\) 这条边到达更高的点，也就说明 \(x\) 点并不是一个边双的起点。
• 若 \(dfn_v<dfn_x(e \in 非树边)\)，说明 \(x\) 可以通过非树边到达更高的点，所以 \(x\) 为某个边连通图的 \(dfn\) 最小的点，但其不会是一个边双的起点。

综上，又因为 \(low_x=dfn_x\)，所以当 \(low_x\) 遍历完所有子树但仍未被更新的时候，说明其为一个边双的起点，此时一直出栈直到该点即可。

点双

点双似乎也可以使用 dfs 每遇到割点分割点双，进行求解，但是细节较多，所以一般使用栈存储。

当 \(low_{son_x}=dfn_x\) 时，说明该 \(x\) 是一个点双的起点。若 \(low_{son_x}<dfn_x\)，见边双证明过程，\(x\) 一定不是包含 \(x\) 与 \(son_x\) 的点双的起点。若 \(dfn_v<dfn_x\)，\(x\) 能到达 \(dfn\) 更小的点，但是 \(x\) 的儿子在不通过 \(x\) 的情况下无法到达，所以这些边不影响 \(x\) 是否能成为一个包含 \(x\) 与 \(son_x\) 的点双起点。

当 \(x\) 是两个点双的起点时，属于两个点双的两棵子树一定不连通，因为子树之间没有祖先后代关系，由性质 \(1\) 可以证明。所以在遍历完一棵子树的时候若 \(low_{son_x}=dfn_x\) 便可出栈。注意，由于 \(x\) 可能属于多个点双，所以不必把 \(x\) 出栈。

注意当遍历到根的时候，如果根没有儿子，记得也要将其单独计入一个点双。

void tar(int u){
	int son=0;
	dfn[u]=low[u]=++dn;
	s.push(u);
	for(int i=head[u];i;i=nxt[i]){
		int dao=ver[i];
		if(!dfn[dao]){
			tar(dao);
			son++;
			low[u]=min(low[u],low[dao]);
			if(low[dao]>=dfn[u]){
				sum++;
				int x;
				while(x!=dao){
					x=s.top();
					s.pop();
					ans[sum].push_back(x);
				}
				ans[sum].push_back(u);
			}
		}else low[u]=min(low[u],dfn[dao]);
	}
	if(rt==u&&son==0) ans[++sum].push_back(u);
}

有向图连通分量

定义

给定一个有向图 \(G=(V,E)\)中，若存在点 \(r\)，满足从 \(r\) 除法能够到达 \(V\) 中所有的点。则称 \(G\) 是一张流图，简记为 \((G,r)\)

在一个流图上从 \(r\) 出发进行深度优先遍历，每个点只访问一次，则发生递归的边组成一棵由 \(r\) 为根的树，我们将这棵树称为流图 \((G,r)\) 的搜索树。

在深度优先遍历的时候，按照每个点第一次被访问的时间给予流图中 \(N\) 个节点 \(1\) 至 \(N\) 的整数标记，该标记被称为时间戳，记为 \(dfn_x\)。

我们将有向图的边 \((x,y)\) 分为四种：

• 树枝边，即搜索树上的边，\(x\) 是 \(y\) 的父节点。
• 前向边，\(x\) 是 \(y\) 的祖先节点，有时候也叫返祖边。
• 后向边，\(y\) 是 \(x\) 的祖先节点。
• 横叉边，即上述三种情况以外的边，满足 \(dfn_y<dfn_x\)。注意，无向图的搜索树中没有横叉边，详见性质 \(1\)。

给定一张流图，若其中任意两个点 \(u,v\) 都能互相到达，就称这张流图为强连通图。继而，给定一张有向图，其中极大的强连通子图称为强连通分量，简称 “SCC”。

有向图中的 Tarjan 算法

在有向图中，Tarjan 可以求解强连通分量，继而可以缩点，缩点之后原图转化为一个 DAG，于是就会有一些性质可以帮助解题。

强连通分量

性质 \(1\)

强连通具有传递性。比如两个点 \(u,v\) 能互相到达，若 \(v,k\) 也能互相到达，则 \(u,k\) 能互相到达。

证明：显然。

性质 \(2\)

由性质 \(1\) 得到，每个点只属于一个强连通分量。

证明：反证，若一个点属于多个强连通分量中，那么根据传递性，这两个强连通分量可以合并，其就不是极大的了，故原假设不成立。

类似于求解边双与点双，一个环肯定是强连通分量，所以我们可以使用栈储存点，当回溯的起点的时候，就一直出栈一直到起点。由于每个点只属于一个强连通分量，所以可以搜索完所有的子树后再检查当前位置是否是起点，然后出栈，类似于边双而非点双。判断其是否是起点与点双和边双相同，也是如果 \(dfn_u=low_u\)，其就是起点。

先说 \(low\) 数组也就是类似 \(dp\) 数组的含义与更新。\(low\) 在有向图中的含义与在无向图中有所不同。在有向图中 \(low_x\) 的含义为 \(x\) 节点能到达的且会和其在同一个强连通分量的点的最小 \(dfn\)。这是因为在无向图中，若 \(x\) 遍历到了一条边的终点的 \(dfn\) 小于 \(dfn_x\)，因为无向图没有横叉边，所以这条边一定是返祖边，则 \(x\) 与该点一定形成一个环，故这两个点既在一个边双又在一个点双中。而在有向图中，遇到了一条边的终点的 \(dfn_v<dfn_x\)，这条边可能为横叉边，如下图：

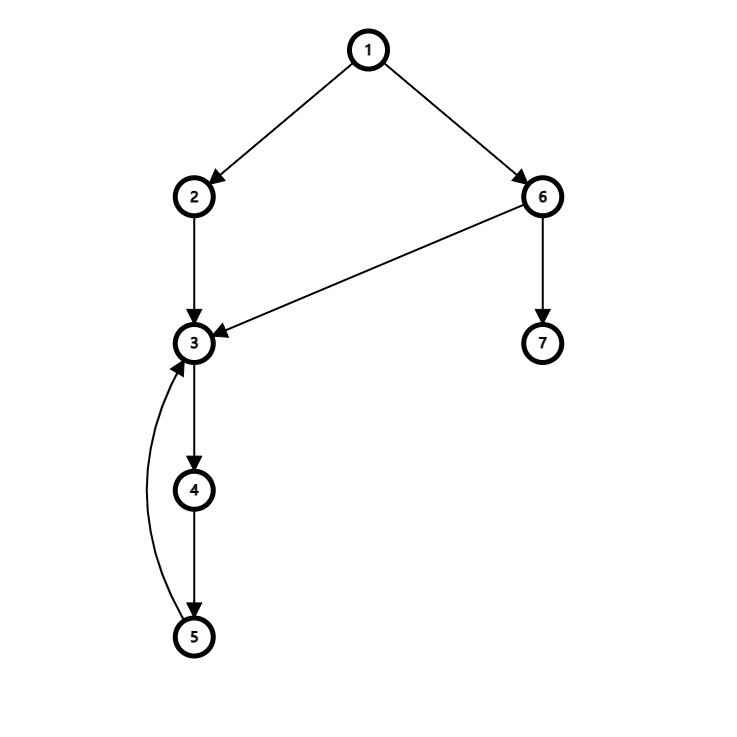
若先遍历到了 \(2,3,4,5\)，然后是 \(6\)，则 \((6,3)\) 这条边 \(dfn_3<dfn_6\)，但是由于 \(3\) 已经确定了自己的强连通分量，所以 \(6\) 和 \(3\) 一定不在一个强连通分量里面，如果强行更新的话，会导致判断强连通分量的起点错误。

以上是 \(low\) 数组新的定义，下文讲解 \(low\) 数组的更新。

当遇见横叉边 \((u,v)\) 的时候，如果 \(v\) 已经不在栈中了，说明 \(v\) 点已经出栈，其已经找到了自己的强连通分量，所以 \(u\) 与 \(v\) 一定不在一个强连通分量中。所以更新的时候的前提条件是 \(v\) 在栈中，而 \(v\) 在栈中说明 \(v\) 所属的强连通分量起点在 \(lca(u,v)\) 以上，所以 \(v\) 一定能通过若干个横叉边与后向边，最后通过若干个前向边或树枝边到达 \(lca(u,v)\) 继而向下到达 \(u\)。所以此时 \(low_u=min(low_u,low_v)\) 或者 \(low_u=min(low_u,dfn_v)\) 都是可以的，因为无论是哪种更新 \(low_u>dfn_{强连通分量起点}\)。

当遇到树枝边，将 \(low_x=min(low_x,low_{son_x})\)。因为如果 \(low_{son_x}\) 如果小于 \(dfn_x\)，则可以将 \((x,son_x)\) 看成在栈中的横叉边，两者一定在一个强连通分量。但一定要取 \(low_{son_x}\)，因为 \(low\) 数组的含义是能到达最小的 \(dfn\)。

当遇到后向边 \((u,v)\) 的时候，也可以将 \((u,v)\) 看成在栈中的横叉边。按照横叉边更新即可。

void dfs(int u){
	dfn[u]=++dn,low[u]=dn,vis[u]=true;
	s.push(u);
	for(int i=head[u];i;i=nxt[i]){
		int dao=ver[i];
		if(!low[dao]){
			dfs(dao);
			low[u]=min(low[u],low[dao]);
		}else if(vis[dao]) low[u]=min(low[u],dfn[dao]);
	}
	if(low[u]==dfn[u]){
		bcnt++;
		while(s.top()!=u)
			bein[s.top()]=bcnt,ans[bcnt].push_back(s.top()),vis[s.top()]=false,s.pop();
		bein[s.top()]=bcnt,ans[bcnt].push_back(s.top()),vis[s.top()]=false,s.pop();
	}
}

缩点

缩点就是将一个强连通分量缩成一个点，由于缩完点后的图上如果有环就说明仍然有强连通分量存在，所以缩完点后的图一定是一个 DAG（有向无环图），此时有一些好的性质可以在题中利用，或者在这个图上做 dp。如下题：缩点模板。

由于这个题可以重复经过点，所以处于同一个强连通分量的点只要选取了一个，那么整个分量都可以选上，缩点之后相当于一个 DAG，拓扑一下然后在 DAG 做一个简单 dp 即可。

现在问题来到怎么建立缩点后的新图。由于已经求出了强连通分量，所以可以再次进行 dfs，如果一条有向边连接的两个点不属于一个强连通分量，那就在这两个强连通分量上连一条有向边即可。

void dfs1(int u){
	vis[u]=true;
	for(int i=head[u];i;i=nxt[i]){
		int dao=ver[i];
		if(!vis[dao]) dfs1(dao);
		if(bein[dao]==bein[u]) continue;
		g[bein[u]].push_back(bein[dao]);
	}
}

2-SAT

这个就有点像强连通分量的扩展了。这类型的题目大意为给定长度 \(n\)，求出满足 \(k\) 个形如若 \(a_x=p\) 则 \(a_y=q\) 的限制条件的布尔序列的一种解。

首先考虑什么情况无解，显然当 \(a_x=0\) 能推出来 \(a_x=1\) 且当 \(a_x=1\) 能推出来 \(a_x=0\) 的时候无解，即两者可以互相推出。这就类似一个强连通分量，所以我们考虑建图。

我们将每个点看成两个，分别为 \(i\) 与 \(i+n\)，\(i\) 号节点代表下标为 \(i\) 的值是 \(0\)，\(i+n\) 代表下标为 \(i\) 的值是 \(1\)。则原先的条件可以转化成 \(x+p \times n\) 向 \(y+q \times n\) 连一条有向边。然而我们发现当 \(a_y=p\) 的时候，\(a_x\) 必须为 \(q\)。这就是其的逆否命题，应当也将逆否命题看成一条限制来连边。

则无解的条件转化为 \(i\) 和 \(i+n\) 节点在一个强连通分量的时候无解。否则进行拓扑排序，后出现的节点就是下标为 \(i\) 的值如果是先出现的节点的话，有可能推出来另外一个节点，也就互相矛盾了。

接下来需要证明同一个强连通分量中的节点要不然都比与自己对应的另外一个节点的拓扑序小，要不然比他们大。这样可以保证同一个强连通分量的取值是一致的。

由于一个限制条件同时有逆否命题，故一个强连通分量对应的另外的节点也会形成强连通分量，故两者一定不会出现拓扑序大小不同的情况。证毕。

以上就是本次图论连通分量的笔记。