线段树优化建图

适用范围

当一张图边数较多且建边的对象是区间时，可以使用线段树优化建图。

例题

CF786B Legacy

首先将方案转化为在图上建边，将方案的价值转化为边权。则问题变为有 \(q\) 次操作，每次操作可以从点向区间的点连边，或从区间向点连边，或点向点连边，求 \(s\) 点到所有点的最短路。

发现总共有 \(q \times n\) 条边，直接建边肯定会超时，但是边的对象是区间，所以想到线段树。

将区间放在线段树上最多有 \(\log n\) 个节点，那么总共就只剩下 \(q \times \log n\) 条边，可以接受。

该如何建图呢，下图是一个示例，点 \(7\) 连向区间 \(1\) 至 \(3\)。

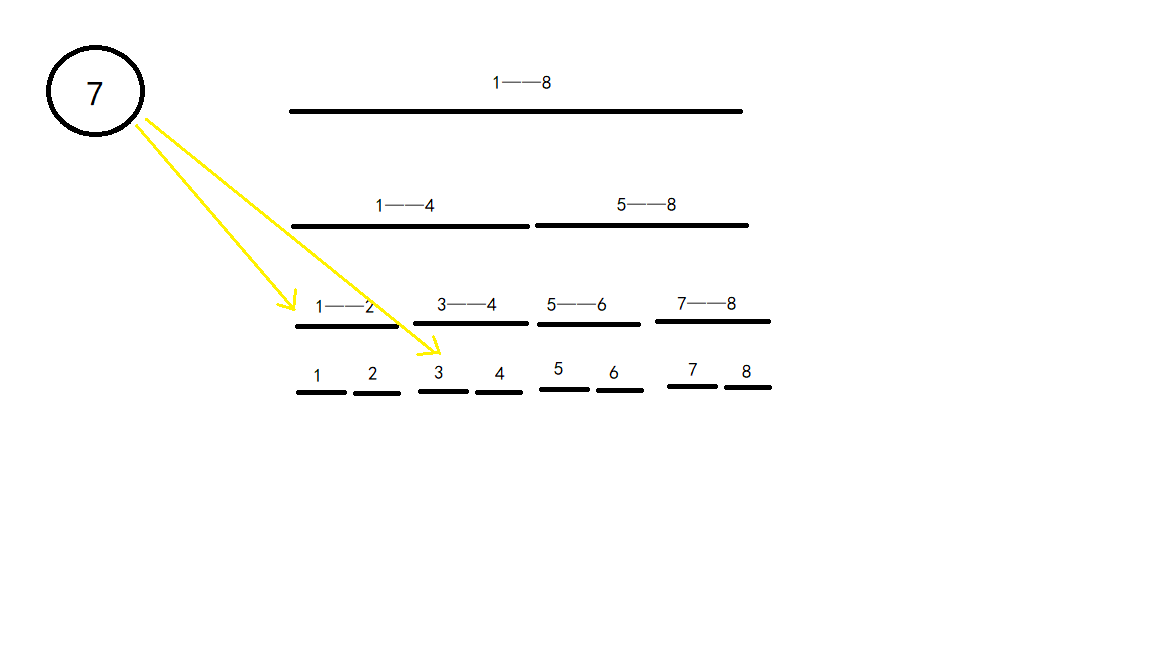
但是区间本质由点组成，所以点 \(7\) 是需要连到节点上的，那就让线段树向下连。

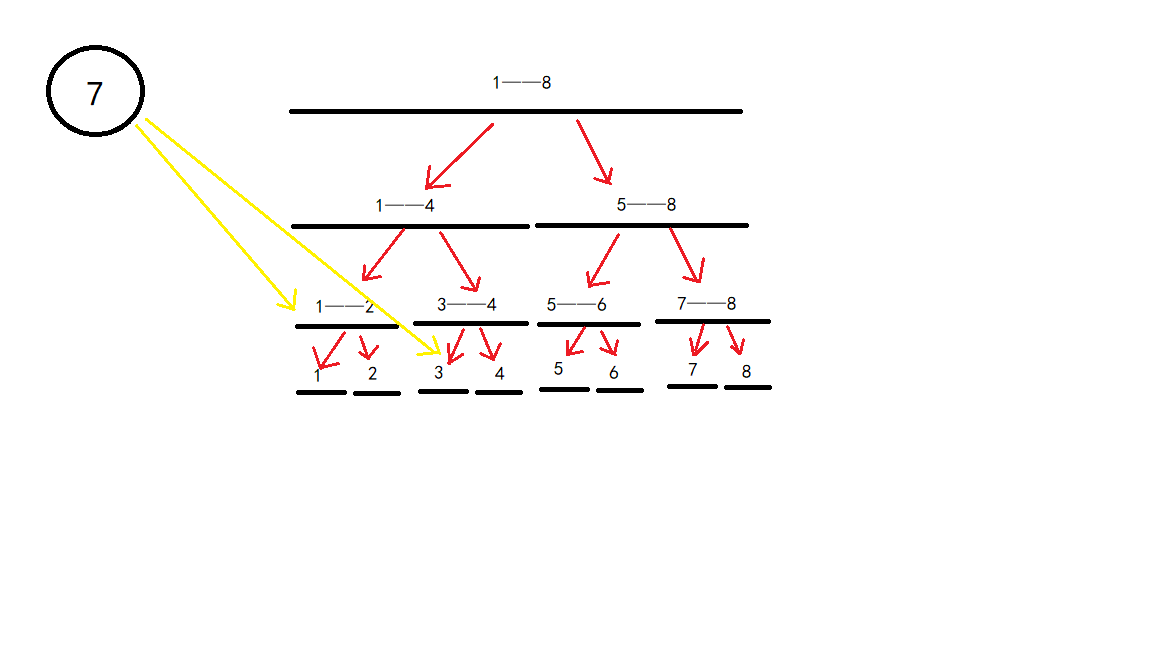
这样我们就完成了从点连向区间了，那该如何从区间连向点呢？我们想到可以依然用这棵线段树，将其从下向上连边，然后连向一个节点，就像这样（只画了 \(1\) 至 \(4\)）：

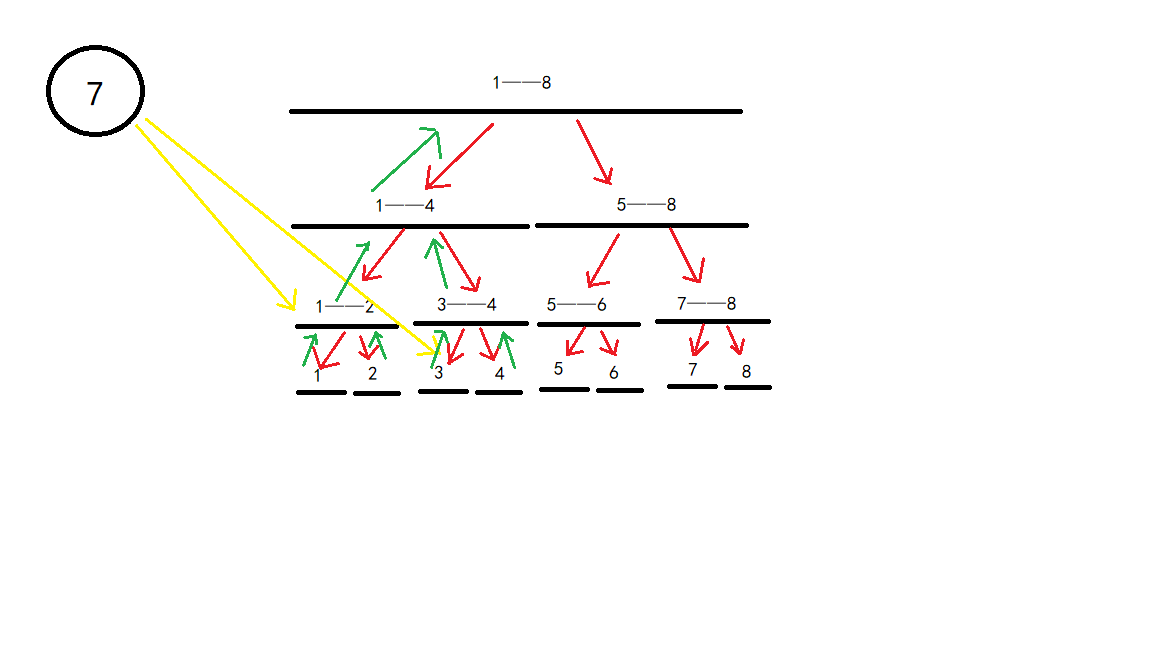
但是此时由于红边与绿边的边权都是 \(0\)，则任何点都能通过红边与绿边用 \(0\) 代价到达任意地方，于是想到可以建立两棵线段树，一个从上向下连边，代表从点连向区间；一个从下向上连边，代表从区间连向点。下图是 \(8\) 号点连向 \(1\) 至 \(6\) 的区间。

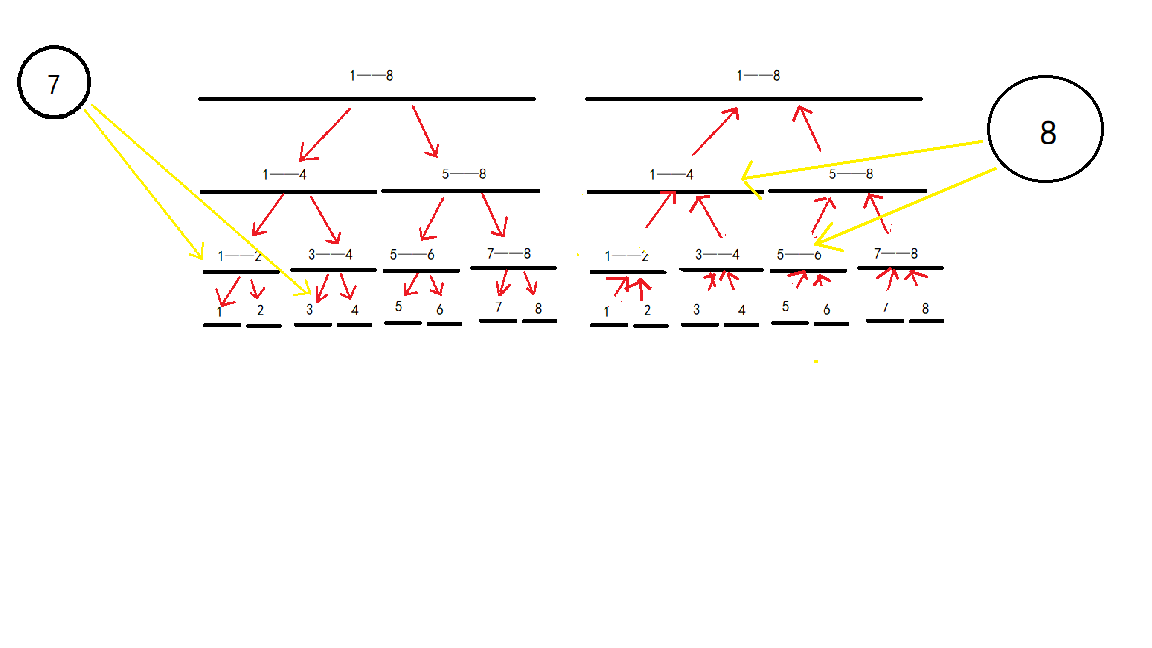
由于两棵线段树的叶子节点本质相同，所以两个叶子节点中间连一条边权为 \(0\) 的无向边。

然而我们还需要新建一个数组来表示一个节点，然后将其连向线段树，太不优美了。所以可以将第二棵线段树上的叶子节点连向第一棵线段树，表示点连向区间；将第二棵线段树连向第一棵线段树上的点，代表区间连向点。这样就成功建完图了。

建完图之后就简单了，跑一遍 dijkstra 就可以了。

ACcode

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (int)(1e18)
#define mid (l+r>>1)

const int N=1e5+10;

int n,Q,st,idx,sum;
int siz[N],dis[N<<5],vis[N<<5];
int head[N<<5],nxt[N<<5],ver[N<<5],val[N<<5];

//第一棵线段树从上到下，别连接其相当于别连接一个区间 
//第二棵线段树从下到上，其连接别相当于一个区间连接别 

inline int read(){
	int t=0,f=1;
	register char c=getchar();
	while(c<'0'||c>'9') f=(c=='-')?(-1):(f),c=getchar();
	while(c>='0'&&c<='9') t=(t<<3)+(t<<1)+(c^48),c=getchar();
	return t*f;
}

void add(int u,int v,int w){
	nxt[++idx]=head[u];
	head[u]=idx;
	ver[idx]=v;
	val[idx]=w;
}

void init(int bian,int l,int r){
	sum=max(sum,bian);
	if(l==r) return;
	init(bian<<1,l,mid);
	init(bian<<1|1,mid+1,r);
}

void build(int bian,int l,int r){
	if(l==r){add(bian,bian+sum,0),add(bian+sum,bian,0);return;}
	add(bian,bian<<1,0),add(bian,bian<<1|1,0);
	add((bian<<1)+sum,bian+sum,0),add((bian<<1|1)+sum,bian+sum,0);
	build(bian<<1,l,mid);build(bian<<1|1,mid+1,r);
}

int find(int bian,int l,int r,int x){
	if(l==r) return bian;
	if(x<=mid) return find(bian<<1,l,mid,x);
	else return find(bian<<1|1,mid+1,r,x);
}

void ins(int bian,int l,int r,int L,int R,int x,int y,bool flag){
	if(L<=l&&R>=r){
		if(!flag) add(x,bian,y);
		else add(bian+sum,x,y);
		return;
	}
	if(L<=mid) ins(bian<<1,l,mid,L,R,x,y,flag);
	if(R>mid) ins(bian<<1|1,mid+1,r,L,R,x,y,flag);
}

priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q; 

void dij(){
	for(int i=1;i<=sum*2;i++) dis[i]=INT_MAX;
	dis[st]=0,q.push({dis[st],st});
	while(!q.empty()){
		pair<int,int> x=q.top();q.pop();
		vis[x.second]=true;
		for(int i=head[x.second];i;i=nxt[i]){
			int dao=ver[i];
			if(dis[dao]>x.first+val[i]){
				dis[dao]=x.first+val[i];
				if(vis[dao]) continue;
				q.push({dis[dao],dao});
			}
		}
	}
}

void Get_ans(int bian,int l,int r){
	if(l==r){
		if(dis[bian]==INT_MAX) cout<<-1<<" ";
		else cout<<dis[bian]<<" ";
		return;
	}
	Get_ans(bian<<1,l,mid);
	Get_ans(bian<<1|1,mid+1,r);
}

signed main(){
	n=read(),Q=read(),st=read();
	init(1,1,n);build(1,1,n);
	for(int i=1;i<=Q;i++){
		int op=read();
		if(op==1){
			int u=read(),v=read(),w=read();
			int fu=find(1,1,n,u),fv=find(1,1,n,v);
			add(fu,fv,w); 
		}else{
			int u=read(),l=read(),r=read(),w=read();
			ins(1,1,n,l,r,find(1,1,n,u),w,op-2);
		}
	}st=find(1,1,n,st);
	dij();Get_ans(1,1,n);
	return 0;
}