线段树合并
使用范围
当一棵树需要将儿子的信息合并时，且总信息量不多的时候，可以用线段树合并节省时间复杂度。
例题
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
如果要使用线段树合并，直接树链剖分将 \(x\) 到 \(y\) 的路径加上救济粮肯定是不行的。因为线段树合并的时候要求合并的东西是一棵树，而树链剖分则将树变成链。而且如果直接将路径全部加上救济粮，父节点就不能从子儿子转移，也就不会合并了。
所以考虑换一种思路，将操作改为在差分数组上操作，将 \(x\) 到 \(y\) 的路径加上第 \(z\) 种救济粮就可以改成：
\[tr_{x,z}+1,tr_{y,z}+1,tr_{lca(x,y),z}-1,tr_{fa_{lca(x,y)},z}-1
\]
发现此时每个点会维护有 \(z\) 个点的信息，即每种救济粮有多少袋。而父节点维护的信息需要从儿子节点转移。现在看起来很难转移，但是总信息其实总共并不多，只有 \(4 \times m\) 个信息。所以可以对每个点建一个动态开点线段树，每个信息只会影响一条链即 \(\log n\) 的点。现在考虑如何将一群儿子的线段树合并到父节点上。
如图，左边是父节点的线段树，右边是一个子儿子的线段树。合并的时候从根节点开始遍历。
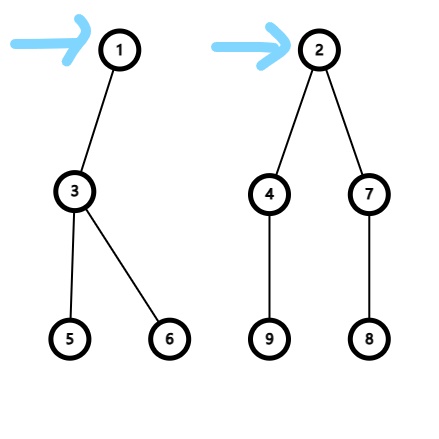
先向左边遍历，两者都有节点，继续遍历。
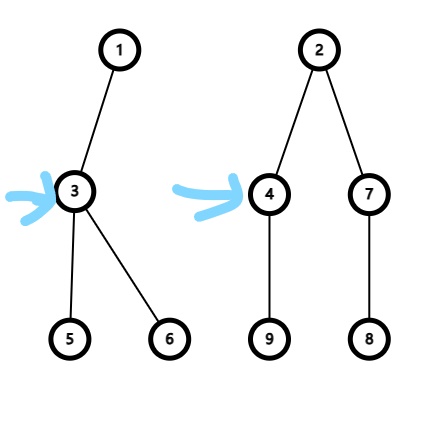
向左边发现当前是叶子节点，则将儿子的节点值加到父亲上。回到父节点，向右边遍历，发现此时儿子当前位置没有节点，那就直接回到父节点，因为此时向下一定不会改变父节点的值。
回到根节点，向右遍历。
发现此时父亲该位置没有节点，那就直接将儿子的节点接到父亲上，类似主席树。
遍历结束。
此时就把一个儿子的树合并到了父节点上，其他儿子依次类推。
合并完成答案就很好求了，直接求出最大值就行了。
ACcode
注意一个细节，应当先合并，再加入自己节点的信息，这样既可以节省时间，又可以节省空间。
#include <bits/stdc++.h>
using namespace std;
#define INT_MAX (int)(1e18)
#define mid (l+r>>1)
#define pr pair<int,int>
const int N=1e5+10;
const int Maxx=1e5;
int n,m,idx;
int head[N],nxt[2*N],ver[2*N];
int bei[20][N],dep[N],fa[N],ans[N];
vector<pr> g[N];
struct Tree{
int cnt;
struct node{
int l,r,val,wei;
}tr[N<<5];
void pushup(int bian){
int l=tr[bian].l,r=tr[bian].r;
if(tr[l].val>tr[r].val) tr[bian].wei=tr[l].wei;
else if(tr[l].val<tr[r].val) tr[bian].wei=tr[r].wei;
else tr[bian].wei=min(tr[l].wei,tr[r].wei);
tr[bian].val=max(tr[l].val,tr[r].val);
}
int merge(int p1,int p2,int l,int r){
if(!p1||!p2) return p1|p2;
if(l==r){tr[p1].val+=tr[p2].val;return p1;}
tr[p1].l=merge(tr[p1].l,tr[p2].l,l,mid);
tr[p1].r=merge(tr[p1].r,tr[p2].r,mid+1,r);
pushup(p1);return p1;
}
int insert(int bian,int l,int r,int x,int y){
if(!bian) bian=++cnt;
if(l==r){tr[bian].wei=l,tr[bian].val+=y;return bian;}
if(x<=mid) tr[bian].l=insert(tr[bian].l,l,mid,x,y);
else tr[bian].r=insert(tr[bian].r,mid+1,r,x,y);
pushup(bian);return bian;
}
}Tr;
inline int read(){
int t=0,f=1;
register char c=getchar();
while(c<'0'||c>'9') f=(c=='-')?(-1):(f),c=getchar();
while(c>='0'&&c<='9') t=(t<<3)+(t<<1)+(c^48),c=getchar();
return t*f;
}
void add(int u,int v){
nxt[++idx]=head[u];
head[u]=idx;
ver[idx]=v;
}
void dfs(int u,int v){
fa[u]=v,bei[0][u]=v,dep[u]=dep[v]+1;
for(int i=1;i<=18;i++) bei[i][u]=bei[i-1][bei[i-1][u]];
for(int i=head[u];i;i=nxt[i]){
int dao=ver[i];
if(dao==v) continue;
dfs(dao,u);
}
}
int lca(int u,int v){
if(dep[u]>dep[v]) swap(u,v);
for(int i=18;i>=0;i--)
if(dep[u]<=dep[bei[i][v]]) v=bei[i][v];
if(v==u) return u;
for(int i=18;i>=0;i--)
if(bei[i][u]!=bei[i][v]) u=bei[i][u],v=bei[i][v];
return fa[u];
}
void Merge(int u,int v){
for(int i=head[u];i;i=nxt[i]){
int dao=ver[i];
if(dao==v) continue;
Merge(dao,u);
Tr.merge(u,dao,1,Maxx);
}
for(auto i:g[u]) Tr.insert(u,1,Maxx,i.first,i.second);
ans[u]=Tr.tr[u].wei;
}
signed main(){
n=read(),m=read();Tr.cnt=n;
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v);add(v,u);
}
dfs(1,0);
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
g[u].push_back({w,1});
g[v].push_back({w,1});
int Lca=lca(u,v);
g[Lca].push_back({w,-1});
g[fa[Lca]].push_back({w,-1});
}
Merge(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
return 0;
}
时间复杂度分析
现在我们已经知道了线段树合并的伟大，来分析一下时间复杂度。发现合并的时候时间复杂度是重叠部分大小，那最坏情况就是全部重叠。每个信息会新建 \(\log n\) 个点，每个点最坏合并次数是其深度，深度最大为 \(\log n\)，所以最坏情况是在满二叉树下，信息全放在叶子节点且放置的线段树位置都相同，此时是 \(O(n \log ^ 2 n)\)。
但是真的是这样吗？
发现合并的时候假如两棵树都有节点，那么必然会删去一个节点，所以时间复杂度与删去的节点数量同级，均摊下来即是点的个数，即为 \(n \log n\)。
例题 2
P5298 [PKUWC2018] Minimax
先将权值离散化，想要进行线段树合并，需要父节点能从子节点转移，树形 DP 与之十分相配。
考虑树形 DP，设 \(f_{u,i}\) 表示 \(u\) 节点权值是 \(i\) 的概率 \(D\)，总共有 \(n\) 个叶子节点。显然有：
\[f_{u,i}=f_{l,i} \times (p_u \times \sum_{j=1}^{i-1} f_{r,j} + (1-p_u) \times \sum_{j=i+1}^n f_{r,j}) + f_{r,i} \times (p_u \times \sum_{j=1}^{i-1} f_{l,j} + (1-p_u) \times \sum_{j=i+1}^n f_{l,j})
\]
这个式子有关区间和，可以用线段树维护。
每个点开一个动态开点线段树维护权值是 \(1\) 至 \(n\) 的概率，然后可以进行线段树合并。
注意这题合并的时候遇到接节点时，乘值需要打上一个懒标记，因为是区间乘值。
ACcode
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INT_MAX (int)(1e18)
#define mid (l+r>>1)
const int N=3e5+10;
const int mod=998244353;
int n,m,idx,len,ans;
int head[N],nxt[N],ver[N];
int val[N],son[N],li[N];
struct Tree{
int cnt;
struct node{
int l,r,val,lan;
}tr[N<<5];
int rv(int x){return (1-x+mod)%mod;}
void pushup(int bian){tr[bian].val=(tr[tr[bian].l].val+tr[tr[bian].r].val)%mod;}
void tag(int bian,int x){tr[bian].val=tr[bian].val*x%mod,tr[bian].lan=tr[bian].lan*x%mod;}
void pushdown(int bian){
int l=tr[bian].l,r=tr[bian].r;
if(l) tag(l,tr[bian].lan);
if(r) tag(r,tr[bian].lan);
tr[bian].lan=1;
}
int merge(int u1,int u2,int l,int r,int lq,int lh,int rq,int rh,int x){
if(!u1){if(lh||lq) tag(u2,(lh*rv(x)%mod+lq*x%mod)%mod);return u2;}
if(!u2){if(rh||rq) tag(u1,(rh*rv(x)%mod+rq*x%mod)%mod);return u1;}
//l=r 的时候 f 一定等于 1
pushdown(u1),pushdown(u2);
int u1r=tr[tr[u1].r].val,u2r=tr[tr[u2].r].val,u1l=tr[tr[u1].l].val,u2l=tr[tr[u2].l].val;
tr[u1].l=merge(tr[u1].l,tr[u2].l,l,mid,lq,(lh+u1r)%mod,rq,(rh+u2r)%mod,x);
tr[u1].r=merge(tr[u1].r,tr[u2].r,mid+1,r,(lq+u1l)%mod,lh,(rq+u2l)%mod,rh,x);
pushup(u1);return u1;
}
int ins(int bian,int l,int r,int x){
if(!bian) bian=++cnt;
if(l==r){tr[bian].val=1;return bian;}
pushdown(bian);
if(x<=mid) tr[bian].l=ins(tr[bian].l,l,mid,x);
else tr[bian].r=ins(tr[bian].r,mid+1,r,x);
pushup(bian);return bian;
}
void query(int bian,int l,int r){
if(l==r){
ans=(ans+l*li[l]%mod*tr[bian].val%mod*tr[bian].val%mod)%mod;
return;
}
pushdown(bian);
query(tr[bian].l,l,mid);
query(tr[bian].r,mid+1,r);
}
}Tr;
inline int read(){
int t=0,f=1;
register char c=getchar();
while(c<'0'||c>'9') f=(c=='-')?(-1):(f),c=getchar();
while(c>='0'&&c<='9') t=(t<<3)+(t<<1)+(c^48),c=getchar();
return t*f;
}
void add(int u,int v){
nxt[++idx]=head[u];
head[u]=idx;
ver[idx]=v;
}
int ksm(int x,int y){
int sum=1;
while(y){
if(y&1) sum=sum*x%mod;
x=x*x%mod,y>>=1;
}
return sum;
}
void dfs(int u,int v){
for(int i=head[u];i;i=nxt[i]){
int dao=ver[i];
if(dao==v) continue;
dfs(dao,u);Tr.merge(u,dao,1,len,0,0,0,0,val[u]);
}
if(!son[u]) Tr.ins(u,1,len,(lower_bound(li+1,li+1+len,val[u])-li));
}
signed main(){
n=read();Tr.cnt=n;
for(int i=1;i<=n;i++){
int u=read();
add(u,i);son[u]++;
}
for(int i=1;i<=n;i++){
val[i]=read();
if(!son[i]) li[++len]=val[i];
else val[i]=val[i]*ksm(10000,mod-2)%mod;
}
sort(li+1,li+1+len);
dfs(1,0);Tr.query(1,1,len);
cout<<ans<<"\n";
return 0;
}
浙公网安备 33010602011771号