线段树从入门到放弃QAQ
最近学习了线段树这一初级数据结构,本蒟蒻现总结一下近期的学习成果。
#define lt i<<1
#define rt i<<1|1
struct node{ int l,r; long long sum,lz; }tree[300001];
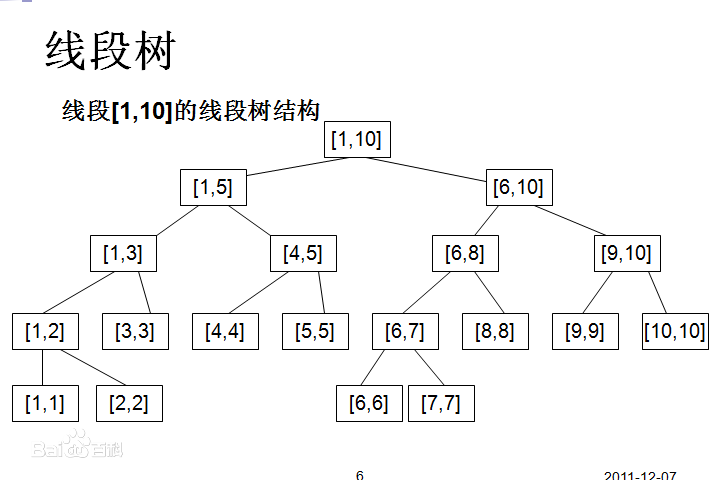
inline void build(int i,int l ,int r) { tree[i].l=l; tree[i].r=r; if(l==r) { tree[i].sum = a[l]; return ; } int mid = (l+r)>>1; build(lt,l,mid); build(rt,mid+1,r); tree[i].sum = tree[lt].sum+tree[rt].sum; return ; }
下来就是单点修改:我们自然要搜到对应的那一个点,但需要注意的是,我们包含这个点的所有区间对应的节点的sum都应该进行改变,解决方法就是在递归返回的当前这一层的时候记得再算一次sum
inline void add(int v,int i, int pos) { if(tree[i].l==tree[i].r) { tree[i].sum+=v; return ; } if(pos<=tree[lt].r) add(v,lt,pos); else add(v,rt,pos); tree[i].sum=tree[lt].sum+tree[rt].sum; return ; }
在介绍区间修改之前,我们需要先介绍一个叫lazy_tag的东西和push_down的操作,它可以帮助我们更好的解决区间操作问题
先上代码:
inline void push_down(int i) { if(tree[i].lz) { tree[lt].sum += tree[i].lz*(tree[lt].r-tree[lt].l+1); tree[rt].sum += tree[i].lz*(tree[rt].r-tree[rt].l+1); tree[lt].lz+=tree[i].lz; tree[rt].lz+= tree[i].lz; tree[i].lz=0; } }
每一个节点都有一个lz标记,它是用来干什么的呢?
我们对区间进行修改的时候我们不必每一次都修改到对应的叶节点上,即一个个孤立的点,我们这样考虑,如果一个区间恰好包含在目标区间之内,我们的修改就停止在这一层,并给他打上lz标记,同时它的sum需要更新,即从上面传下来的lz*区间长度(注意这里lz仅是从上传下来的,不包含他已经有的lz)。如果当前区间并未完全包含,我们就向下传lz并更新它下方节点,同时清空lz。注意,每队一个区间进行递归操作时,最后都要在求一次和!!! t同时我们向下继续操作时的判断条件需要注意 这样做有什么好处呢?别急先上代码
区间修改:
inline void rangeadd(int i,int l, int r, long long v) { if(tree[i].l>=l&&tree[i].r<=r) { tree[i].sum+=v*(tree[i].r-tree[i].l+1); tree[i].lz+=v; return ; } push_down(i); if(tree[lt].r>=l) rangeadd(lt,l,r,v); if(tree[rt].l<=r) rangeadd(rt,l,r,v); tree[i].sum=tree[lt].sum+tree[rt].sum; }
区间查询:
inline long long rangesearch(int i, int l ,int r) { if(tree[i].l>=l&&tree[i].r<=r) return tree[i].sum; if(tree[i].l>r||tree[i].r<l) return 0; push_down(i); long long s=0; if(tree[lt].r>=l) s+=rangesearch(lt,l,r); if(tree[rt].l<=r) s+=rangesearch(rt,l,r); return s; }
有了lz标记后,我们对区间查询时,如果当前节点没有lz,就直接向下搜,否则将lz标记向下打,同时注意查询的判断,最终我们就可以得到区间sum。
我们发现,利用lz标记,我们无需每次都递归到底,而是用了一种代替的方法,如果不用递归到底,谁又愿意去递归呢-bzzb 只需在查询时,如果需要,我们不妨再去做出改变
ok 线段树的基本操作就介绍完毕了,读者可以做一做洛谷的 P3372线段树模板1来练练手
2、进阶教程
我们现在尝试构建这样一棵线段树,它支持加法和乘法的修改,我们如何去实现呢?
首先,大体肯定和原来基础线段树差不多,但是我们稍加思考,想到需要改变一下现有的push_down,如何做出改变呢?
我们将加的lz和乘的lz分开,分别定义为plz和mlz,同时注意mlz需要初始化为1,每一次“修改”(这里的修改既指加又指乘)时,我们都需要进行一次push_down,我们先给出代码
乘法线段树:
inline void pushdown(int i){
//没有了判断条件 long long k1=tree[i].mlz,k2=tree[i].plz; tree[lt].sum=(tree[lt].sum*k1+k2*(tree[lt].r-tree[lt].l+1));// tree[rt].sum=(tree[rt].sum*k1+k2*(tree[rt].r-tree[rt].l+1)); tree[lt].mlz=(tree[lt].mlz*k1); tree[rt].mlz=(tree[rt].mlz*k1); tree[lt].plz=(tree[lt].plz*k1+k2); tree[rt].plz=(tree[rt].plz*k1+k2);
tree[i].plz=0;
tree[i].mlz=1;//这里要注意
return ; }
我们注意到其实乘法线段树与普通线段树的差距十分小 上面一段代码不难看懂
根号/除法线段树:首先谈谈出发线段树 给出这样一段区间 1 2 3 4 5 我要让这个区间的每一个数都去除以4 ,这时候我们发现似乎push_down操作行不通了,因为push_down操作可以看作是对一个区间的sum进行操作,而并非每一个确定的叶节点,那么显然1/4+2/4+3/4+4/4+5/4!=(1+2+3+4+5)/4 那么怎么办呢?
我们首先想到了每一个数去除以这个数,但肯定不行,这样不就成了暴力吗。
我们对于每个区间,维护她的最大值和最小值,然后每次修改时,如果这个区间的最大值的商和最小值的商一样,说明这个区间整体除法不会产生误差,就直接修改(根号同理)
这样我们就可以保证不用每一次的操作去操作叶节点了,但有一些操作有是需要的,没办法,似乎也没有能够优化的算法了TAT
代码如下:
inline void Sqrt(int i,int l,int r){ if(tree[i].l>=l && tree[i].r<=r && (tree[i].minn-(long long)sqrt(tree[i].minn))==(tree[i].maxx-(long long)sqrt(tree[i].maxx))){//如果这个区间的最大值最小值一样 long long u=tree[i].minn-(long long)sqrt(tree[i].minn);//计算区间中每个元素需要减去的 tree[i].lz+=u; tree[i].sum-=(tree[i].r-tree[i].l+1)*u; tree[i].minn-=u; tree[i].maxx-=u; return ; } if(tree[i].r<l || tree[i].l>r) return ; push_down(i); if(tree[lt].r>=l) Sqrt(lt,l,r); if(tree[rt].l<=r) Sqrt(rt,l,r); tree[i].sum=tree[lt].sum+tree[rt].sum; tree[i].minn=min(tree[lt].minn,tree[rt].minn);//维护最大值和最小值 tree[i].maxx=max(tree[lt].maxx,tree[rt].maxx); return ; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号