高斯消元法
高斯消元转自:《算法设计与实现》主编 陈宇 吴昊
例题1题解转自:https://www.cnblogs.com/baiyi-destroyer/p/9473064.html
例题2题解转自: https://blog.csdn.net/lianai911/article/details/48464007?biz_id=102&utm_term=Flip%20Game%20%E9%AB%98%E6%96%AF%E6%B6%88%E5%85%83%E6%B3%95&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-48464007&spm=1018.2118.3001. 4187
例题3题解转自:https://blog.csdn.net/bless924295/article/details/53575836
例题4题解转自: https://www.cnblogs.com/ACRykl/p/8711227.html
高斯消元法
一 理论基础
① 高斯消元:解 一个线性方程组,对方程组的增广矩阵施行初等行变换,变换后的矩阵所对应的方程组与原方程组同解。
② 需要用到的理论知识有:增广矩阵,初等行变换,行阶梯形矩阵,矩阵的秩(这些先弄懂再说代码吧)
二,代码实现
1,一些名词的解释:
主元: 每个非零行第一个非零元素
不确定的变元:未知数(想要求解,但不知道能否解出来)
确定的变元:可求解的未知数
自由变元:无法求解的未知数
2, 根据题意列出方程组,然后根据方程组构造增广矩阵
for (int i = 0; i < ROW; i++) // 增广矩阵
for (int j = 0; j < COL + 1; j++) // 要加上常数项向量
scanf("%d", &a[i][j]);
3,求出每一列的主元,再通过初等行变换将主元以下的元素清零
①,循环:设变量 row,col 指向主元的行与列,将 col 做循环变量,循环系数矩阵的每一列;row 指向当前循环列的主元的行数,用来试探主元的位置,一直循环到主元的位置要越出系数矩阵的界。
②,确定主元:找到当前循环列的最大绝对值,将该元素作为主元,并将该元素所在行移至主元所在行。
③,清零:利用主元所在行,通过初等行变换将主元以下的元素清零。
4,根据矩阵的秩,判断解的情况
①,row 的含义
因为下标从 0 开始,所以化行阶梯型矩阵后,row
代表主元的个数,
代表确定变元的个数,
代表系数矩阵的秩 (注意是循环结束条件,这个是系数矩阵的秩,而不是增广矩阵)
代表阶梯线下方的第一行。(阶梯线之下,系数矩阵全为 0)只看系数矩阵的话:以第 row 行 为分界线,< row 的 全是非零行,>= row 的全是零行(即该行全是零)
②,根据 row ,判断解的情况
无解:当方程中出现(0, 0, …, 0, a)的形式,且a != 0时,说明是无解的;row == COL :代表方程组的每一个未知数 刚好可解,即该方程组唯一可解;row < COL:代表方程组的未知数 有些是解不出来的,即该方程组有无穷解(注:row 不可能大于 COL)
③,当方程组为唯一解时,可以通过回带,逐一求出解集
④,当方程组为无穷解时,如何判断哪些变元是自由还是确定的呢?
通过 数组 bool free_x[N]; 判断是否是不确定的变元。free_x[1] == 1 表示 第i个未知数为自由变元,free_x[i] == 0 表示第i个未知数可解首先,自由变元有 COL - row 个。然后我们先把所有的变元视为不确定变元,即 free_x[i] = 1。通过回带,在每一行里尝试求解不确定变元。再判断每一行中不确定变元的个数,如果大于1个,则该行无法求解。如果只有1个变元,那么该变元即可求出,可解的不确定变元 即为确定变元,所以修改为 free_x[i] = 0,最后每一行都循环结束的话,剩下的不确定变元自然都是 自由变元。
5,模板
整数线性方程组的模板

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define N 105 /* 主元: 每个非零行第一个非零元素 不确定的变元:未知数(想要求解,但不知道能否解出来) 确定的变元:可求解的未知数 自由变元:无法求解的未知数 */ int a[N][N]; // 增广矩阵 int x[N]; // 解集 bool free_x[N]; // 判断是否是不确定的变元,free_x[1] == 1 表示 第i个未知数为自由变元,free_x[i] == 0 表示第i个未知数可解 int ROW, COL; // 系数矩阵的 行数,列数 inline int gcd(int a, int b) { return b ? gcd(b, a%b) : a; } inline int lcm(int a, int b) { return a*b / gcd(a, b); } // 高斯消元法解方程组(Gauss-Jordan elimination). // 求解整数线性方程组的模板,浮点数把那个 return -2 去掉,改下数据类型就可 // (-2表示有浮点数解,-1表示无解,0表示唯一解,大于0表示无穷解,并返回自由变元的个数) int Gauss(void) { int row = 0, col = 0; /* 循环目的:求行阶梯形矩阵 col:循环变量,循环系数矩阵的每一列 row 指向当前循环列的主元的行数,它是用来试探主元的位置 循环结束条件是:主元的位置要越系数矩阵的界了 总结起来就是:通过循环每一列,将主元以下的元素清零 */ for (; row < ROW&&col < COL; row++, col++) { // 找到当前循环列的最大绝对值,将该元素所在行移至主元所在行 int k = row; for (int i = row + 1; i < ROW; i++) // 阶梯线上的元素不算 if (abs(a[i][col]) > abs(a[k][col])) k = i; if (k != row) // 交换最大值所在的行到主元行 for (int i = col; i < COL + 1; i++) { int t = a[row][i]; a[row][i] = a[k][i]; a[k][i] = t; } /* 该列(阶梯下方的元素,包括阶梯线上的元素)的最大值为 0,说明阶梯线下方 全为 0 说明该列无主元,则该列不用处理,进入下一列。k-- 是要消去 for循环的++ */ if (a[row][col] == 0) { row--; continue; } // 将当前循环列中,主元以下的元素清零 for (int i = row + 1; i < ROW; i++) { if (a[i][col] != 0) { int LCM = lcm(abs(a[i][col]), abs(a[row][col])); int ta = LCM / abs(a[i][col]); // 被清零行需要乘的倍数 int tb = LCM / abs(a[row][col]); // 主元所在的行需要乘的倍数 if (a[i][col] * a[row][col] > 0) // 同号的话,要弄成异号 tb = -tb; for (int j = col; j < COL + 1; j++) a[i][j] = a[i][j] * ta + a[row][j] * tb; } } } /* 因为下标从 0 开始,所以化行阶梯型矩阵后, row 代表主元的个数,代表确定变元的个数,同时也代表系数矩阵的秩 (注意是循环结束条件,这个是系数矩阵的秩,而不是增广矩阵) 同时,row 也指向阶梯线下方的第一行。(阶梯线之下,系数矩阵全为 0) 只看系数矩阵的话:以第 row 行 为分界线,< row 的 全是非零行,>= row 的全是零行(即该行全是零) */ /* ① 无解:当方程中出现(0, 0, …, 0, a)的形式,且a != 0时,说明是无解的。 系数矩阵出现零行的话,只可能从第 row 行开始, 所以循环零行,再判断一下该行对应的常数项向量的元素是否为 0,即可 */ for (int i = row; i < ROW; i++) { if (a[i][col] != 0) // 判断 当前行对应的常数项向量是否为 0 return -1; } /* 如何判断哪些变元是自由变元呢? 首先,自由变元有 COL - row 个。 我们先把所有的变元视为不确定变元,即 free_x[i] = 1,通过回带,在每一行里尝试求解不确定变元。 首先判断该行中不确定变元的个数,如果大于1个,则该行无法求解。 如果只有1个变元,那么该变元即可求出,可解的不确定变元 即为确定变元,所以修改为 free_x[i] = 0, 最后每一行都循环结束的话,剩下的不确定变元自然都是 自由变元 */ /* ② 无穷解:矩阵的秩 < 未知数的个数 row 代表矩阵的秩:COL 代表未知数的个数 */ if (row < COL) { for (int i = row - 1; i >= 0; i--) // 从下往上循环 行 { int free_x_num = 0; // 用于 记录该行中的不确定的变元的个数 int free_x_c = 0; // 记录 不确定变元的列数 for (int j = 0; j < COL; j++) // 循环 该行中系数矩阵的元素 { if (a[i][j] && free_x[j]) free_x_num++, free_x_c = j; } if (free_x_num > 1) // 该行中的不确定的变元的个数如果超过1个,则无法求解,进入到下一次循环 continue; // 回带 int t = a[i][COL]; // 该行末位的常数项向量中的元素 for (int j = 0; j < COL; j++) { if (a[i][j] && j != free_x_c) // 减去确定变元 t -= a[i][j] * x[j]; } x[free_x_c] = t / a[i][free_x_c]; // 解出这一行中唯一的一个 不确定变元 free_x[free_x_c] = 0; // 不确定变元 被解开 变成确定变元 } return COL - row; } /* ③ 唯一解:矩阵的秩 == 未知数的个数 row 代表矩阵的秩:COL 代表未知数的个数 此时行阶梯阵形成了严格的上三角。(注意这个三角形不一定是沿着对角线的,但它一定是等腰直角三角形,因为系数矩阵不一定是正方形) */ for (int i = row - 1; i >= 0; i--) { int t = a[i][COL]; for (int j = i + 1; j < COL; j++) { if (a[i][j]) // 减去已知变元 t -= -a[i][j] * x[j]; } if (t%a[i][i]) // 说明有浮点数解 return -2; x[i] = t / a[i][i]; } return 0; } int main(void) { while (scanf("%d%d", &ROW, &COL) != EOF) { memset(a, 0, sizeof(a)); memset(x, 0, sizeof(x)); memset(free_x, 1, sizeof(free_x)); // 初始化为 不确定的变元. for (int i = 0; i < ROW; i++) // 增广矩阵 for (int j = 0; j < COL + 1; j++) // 要加上常数项向量 scanf("%d", &a[i][j]); int free_x_num = Gauss(); if (free_x_num == -1) printf("无解!\n"); else if (free_x_num == -2) printf("有浮点数解,无整数解!\n"); else if (free_x_num > 0) { printf("无穷多解!自由变元个数为%d\n", free_x_num); for (int i = 0; i < COL; i++) { if (free_x[i]) printf("x%d 是不确定的\n", i + 1); else printf("x%d:%d\n", i + 1, x[i]); } } else { printf("有唯一解:\n"); for (int i = 0; i < COL; i++) printf("x%d:%d\n", i + 1, x[i]); } } system("pause"); return 0; } /* 无解 3 3 0 0 0 1 0 1 0 1 0 0 1 1 无穷解 3 3 1 0 0 1 0 1 0 1 0 0 0 0 有浮点数解 3 3 2 0 0 1 0 1 0 1 0 0 1 1 唯一解 3 3 1 0 0 1 0 1 0 1 0 0 1 1 */
例题1:
EXTENDED LIGHTS OUT(POJ 1222)
以3x3为例:我们记 L 为待求解的原始布局矩阵,A(i , j) 表示按下第 i 行第 j 列的按钮时的作用范围矩阵,x(i , j) 表示:想要使得 L 回到全灭状态,第 i 行第 j 列的按钮是否需要按下。0表示不按,1表示按下。
L= 0 1 0
1 1 0
0 1 1
A(1 , 1)= A(2 , 2)=
1 1 0 0 1 0
1 0 0 1 1 1
0 0 0 0 1 0
由于灯只有两种状态,所以按下一个按钮,就可以转化成 原始矩阵异或上作用矩阵,或者转化成 原始矩阵加上作用矩阵模2。那么,这个游戏就转化为如下方程的求解:
( L + x(1 , 1)*A(1 , 1) + x(1 , 2)*A(1 , 2) + x(1 , 3)*A(1 , 3) + x(2 , 1)*A(2 , 1) + ... + x(3 , 3)*A(3 , 3) ) %2 = 0
或者是: L ^ x(1 , 1)*A(1 , 1) ^ x(1 , 2)*A(1 , 2) ^ x(1 , 3)*A(1 , 3) ^ x(2 , 1)*A(2 , 1) ^ ... ^ x(3 , 3)*A(3 , 3) = 0
其中 x( i, j ) 是未知数。方程右边的 0 表示零矩阵,表示全灭的状态。直观的理解就是:原来的 L 状态,经过了若干个 A( i, j ) 的变换,最终变成 0,即全灭状态。
两个矩阵异或等于 0 ,说明两个矩阵相等,所以上式可写为:
x(1 , 1)*A(1 , 1) ^ x(1 , 2)*A(1 , 2) ^ x(1 , 3)*A(1 , 3) ^ x(2 , 1)*A(2 , 1) ^ ... ^ x(3 , 3)*A(3 , 3) = L ,(懒的加括号了,异或是最晚算的)
两个矩阵相等,充要条件是矩阵中每个元素都相等,所以只要列出等式,将左右两边的矩阵上的每一个元素对应相等,就可以将上述矩阵转化成了一个9元1次方程组。最后解的:
x(1 , 1) x(1 , 2) x(1 , 3) 1 1 1
x(2 , 1) x(2 , 2) x(2 , 3) = 0 0 0
x(3 , 1) x(3 , 2) x(3 , 3) 0 0 1
也就是说,按下第一行的3个按钮,和右下角的按钮,就全灭了。
回到 题目的 5*6 矩阵,为了 表示方便,我们用 Xi 表示第 i 个按钮是否要按,Li 表示 L 矩阵的第 i 个元素,A(i , j)x: 第 i 行 第 j 列的按钮的作用矩阵 的 第 x 个元素。于是有:(注意 + 和 mod2 的组合 等效于 ^ )
X1*A(1,1)1 + X2*A(1,2)1 + X3*A(1,3)1 +…………+ X30*A(5,6)1 = L1; mod 2
X1*A(1,1)2 + X2*A(1,2)2 + X3*A(1,3)2 +…………+ X30*A(5,6)2 = L2; mod 2
X1*A(1,1)3 + X2*A(1,2)3 + X3*A(1,3)3 +…………+ X30*A(5,6)3 = L3: mod 2
.......
X1*A(1,1)30 + X2*A(1,2)30 + X3*A(1,3)30 +…………X30*A(5,6)30 = L30: mod 2
容易发现,第一行的 A(1,1)1, A(1,2)1,A(1,3)……A(5,6)1,合起来就是 A(1,1) 的全部元素。这是因为 能够影响到当前开关的,当前开关也能影响到它。这里 "影响到当前开关” 指的是:在所有作用矩阵中,在当前开关位置为 1 的作用矩阵对应的开关,“当前开关也能影响到它” 指的是:当前开关对应的作用矩阵能作用于 影响到它的开关。
所以,又有:
X1*A(1,1)1 ^ X2*A(1,1)2 ^ X3*A(1,1)3 ^………^ X30*A(1,1)30 = L1;
X1*A(1,2)1 ^ X2*A(1,2)2 ^ X3*A(1,2)3 ^………^ X30*A(1,2)30 = L2;
X1*A(1,3)1 ^ X2*A(1,3)2 ^ X3*A(1,3)3 ^………^ X30*A(1,3)30 = L3:
........
X1*A(5,6)1 ^ X2*A(5,6)2 ^ X3*A(5,6)3 ^………^ X30*A(5,6)30 = L30:
这就是我们要的增广矩阵。
Plus: 另外一种比较容易记住的看待这个问题的看法:
对于每一个开关,有可能影响到它的因素是:每一个开关是否按下。所以 影响到一个开关的变量有30个,即有:
start ^ ( X1*a1 ^ X2*a2 ^ X3*a3 ^…^ X30*a30 ) = end ;
其中,start 表示 当前开关的初始状态,end 表示当前开关的结束状态,Xi 表示:第 i 个开关是否按下,ai 表示 第 i 个开关按下后是否能影响 当前开关。能够影响到当前开关的,当前开关也能影响到它(上面有解释)。所以 ai,其实就是当前开关的作用矩阵。
所以上式可进一步化为:
X1*a1 + X2*a2 + X3*a3 +…………X30*a30 = end ^ start
所以:30 个开关的系数矩阵是 30*30 的矩阵,第 i 行,第 j 列的元素表示:第 j 个开关是否能够影响到 第 i 个开关,1 表示 可,0 表示 非;每一行的常数项向量为 第 i 个开关的初始状态。
代码:
因为系数矩阵是固定的,所以可以求出秩为30,所以该异或方程组一定有唯一解。

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<math.h> #define N 35 int a[N][N]; // 增广矩阵 int x[N]; // 未知数矩阵 void show(void) { puts(""); for (int i = 0; i < 30; i++) { for (int j = 0; j < 30 + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } // 知道刚好唯一解才能这样写 void Gauss(void) { for (int i = 0; i < 30; i++) // 循环系数矩阵的 列 { if (a[i][i] == 0) // 如果该列的主元为 0 { for (int j = i + 1; j < 30; j++) // 循环主元下面的行,找到随便一个不为零的行,与现在主元位置换行 { if (a[j][i] != 0) { for (int k = i; k < 31; k++) { int t = a[j][k]; a[j][k] = a[i][k]; a[i][k] = t; } break; } } } // 化阶梯 for (int j = 0; j < 30; j++) // 循环当前列的每一个元素 { if (i != j&&a[j][i]) // 如果当前列,除了主元位置,还有的位置 不为 0 { for (int k = i; k < 31; k++) // 循环列,初等行变换 { // 三者等价 //a[j][k] = a[i][k] ^ a[j][k]; a[j][k] = (abs(a[j][k] + a[i][k])) % 2; /* if(a[i][k] == 1) a[j][k] 变号 else if(a[i][k] == 0) a[j][k] 不变 */ } } } } show(); for (int i = 0; i < 30; i++) x[i] = a[i][30]; /* 化成行阶梯形矩阵后,每一行只有一个非零元素,a[i][i],且 a[i][i] == 1, 所以有:1 ^ x[i] = a[i][30], 所以, x[i] = a[i][30] */ } int main(void) { int t; scanf("%d", &t); for (int ii = 0; ii < t; ii++) { // 常数项向量 for (int i = 0; i < 30; i++) scanf("%d", &a[i][30]); // 系数矩阵 for (int i = 0; i < 30; i++) { // 系数矩阵的第i行,是代表灯光的初始状态矩阵L的第i个元素:L[i/6][i%6] 的作用矩阵 A(i/6, i%6) int x0 = i / 6, y0 = i % 6; for (int j = 0; j < 30; j++) { // 作用是相互的,算 当前开关的作用矩阵,相当于算其他能 影响当前开关的开关 int x = j / 6, y = j % 6; if (abs(x - x0) + abs(y - y0) <= 1) // 在作用范围之内的话 a[i][j] = 1; else a[i][j] = 0; } } // show(); Gauss(); printf("PUZZLE #%d\n", ii + 1); for (int i = 0; i < 30; i++) if ((i + 1) % 6 == 0) printf("%d\n", x[i]); else printf("%d ", x[i]); } system("pause"); return 0; }
例题2:
Flip Game(poj 1753)
题解:
1,解的情况
因为系数矩阵是固定的,随所以可求出秩为14,所以可以判断出方程组的解有两种情况: 无穷解和无解。当为无穷解时,自由变元有4个。
( 注意: 0*x1 ^ 0*x2 ^ …… ^ 0*xn = 1 是无解的 )
2,枚举自由变元
该题的思路与上面那题类似,不过多了一步,要枚举自由变元,判断自由变元赋值为多少翻转最少。
怎么枚举呢?
一个自由变元有 0,1 两种情况,该题有 4个自由变元,所以有 16 种情况。我们用 i 从0 循环到 15 , 每一个 i 的二进制对应 对应 1 种情况。如:i = 1 , num = 4,则 i 的二进制为 0001, 则对应的四个自由变元的值 可分别设为 0,0,0,1,此时,方程唯一可解,然后记录此时需要翻动的次数,比较得到最小值即为答案。
3,数组 f[]
int f[N]:用来记录自由变元的行数。f[i]:第 i 个自由变元的列数
记录的两种方法:
① 行阶梯矩阵的同一列主元位置及其下方元素全为 0
if (a[row][col] == 0)
{
row--;
f[free_x_num++] = col;
continue;
}
② 无穷解,无法求解的不确定变元
int cnt = 0;
for (int i = 0; i < COL; i++)
if (free_x[i])
f[cnt++] = i;
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #define inf 0x3f3f3f3f #define N 35 char str[N][N]; int a[N][N]; int free_x[N]; int x[N]; int f[N]; // 记录自由变元的列数,f[i] 表示第 i 个自由变元的列数 int ROW, COL; void show() { puts(""); for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL + 1; j++) printf("%d ", a[i][j]); puts(""); } } void init(char key) // 初始化增广矩阵 { memset(a, 0, sizeof(a)); // 初始化系数矩阵 for (int i = 0; i < ROW; i++) // 循环每个开关 { int x0 = i / 4, y0 = i % 4; for (int j = 0; j < COL; j++) // 循环当前开关的作用矩阵 { int x = j / 4, y = j % 4; if (abs(x0 - x) + abs(y0 - y) <= 1) a[i][j] = 1; } } for (int i = 0; i < ROW; i++) // 初始化 常数项向量 { if (str[i / 4][i % 4] == key) a[i][COL] = 1; } } // 只有 无解 和 无穷解 两种情况 int Gauss(void) { memset(free_x, 1, sizeof(free_x)); memset(x, 0, sizeof(x)); int free_x_num = 0; // 自由变元的个数 int col = 0, row = 0; for (; row < ROW&&col < COL; col++, row++) { int mr = row; for (int i = row + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[mr][col])) mr = i; if (mr != row) for (int i = 0; i < COL + 1; i++) { int t = a[row][i]; a[row][i] = a[mr][i]; a[mr][i] = t; } if (a[row][col] == 0) { row--; f[free_x_num++] = col; continue; } for (int i = 0; i < ROW; i++) // 将该行的其它元素清零 { if (a[i][col] != 0 && i != row) for (int j = col; j < COL + 1; j++) a[i][j] = a[i][j] ^ a[row][j]; // a[i][j] = (a[i][j] - a[k][j] + 2) % 2; } } // printf("%d\n", free_x_num); //show(); for (int i = row; i < ROW; i++) if (a[i][COL] != 0) return -1; return COL - row; // 无穷解 } int fun() { int num = Gauss(); if (num == -1) // 无解 return inf; /* 无穷解 枚举自由变元的可能取值,进而求解方程组 一个自由变元有 0,1 两种情况,所以 num 个自由变元有 2^num 种情况, 每一个 i 的二进制对应 对应 1 种情况 如:i = 1 , num = 4,则 i 的二进制为 0001, 则对应的四个自由变元的值 可分别设为 0,0,0,1 */ int ans = inf; // 在所有情况下,翻转次数最少的 for (int i = 0; i < (1 << num); i++) // 枚举自由变元的所有可能情况 { int cnt = 0; // ① 记录自由变元种中,被赋值为 1 的个数,② 记录解集中为 1 的个数。 两个加起来就是翻转次数了 for (int j = 0; j < num; j++) // 枚举当前情况下,哪几个自由变元被赋值为 1 { if (i&(1 << j)) // 如果 i 的第 j 位为 1 { x[f[j]] = 1; cnt++; } else x[f[j]] = 0; } // 给自由变元赋值后,方程组即唯一可解 for (int j = COL - num - 1; j >= 0; j--) // 枚举阶梯线上的每一行 { // 将该行的系数矩阵的元素乘以他们的解,并将积全都异或起来,就等于该行的常数项,即方程的解 // 反之,将该行的常数项,异或上该行除了主元的元素,就是主元所在列的解 x[j] = a[j][COL]; // 该行的常数项 for (int k = j + 1; k < COL; k++) { if (a[j][k]) // 如果 该元素非零的话 x[j] = x[j] ^ x[k]; } cnt += x[j]; // 解为1,就加1;解为0,就加0 } ans = ans > cnt ? cnt : ans; } return ans; } int main(void) { ROW = COL = 16; for (int i = 0; i < 4; i++) scanf("%s", str[i]); init('b'); int a1 = fun(); init('w'); int a2 = fun(); if (a1 == inf && a2 == inf) printf("Impossible\n"); else printf("%d\n", a1 > a2 ? a2 : a1); system("pause"); return 0; }
例题3:
SETI (POJ 2065)
题解:
思路:若字符串长度为 n,那么这是一个含有n个方程n个未知数的线性方程组,所以只需把相应的系数转为成矩阵解方程组。高斯消元+同余方程+乘法逆元
题目大意:
输入一个素数p和一个字符串s(只包含小写字母和‘*’),字符串中每个字符对应一个数字,'*'对应0,‘a’对应1,‘b’对应2.... 例如str[] = "abc", 那么说明 n=3, 字符串所对应的数列为1, 2, 3。
题目中定义了一个函数:
a0*1^0 + a1*1^1+a2*1^2+........+an-1*1^(n-1) = f(1)(mod p), f(1) = str[0] = a = 1;
a0*2^0 + a1*2^1+a2*2^2+........+an-1*2^(n-1) = f(2)(mod p), f(2) = str[1] = b = 2;
..........
a0*n^0 + a1*n^1+a2*n^2+........+an-1*n^(n-1) = f(n)(mod p),f(n) = str[n-1] = ````
求出 a0,a1,a2....an-1.
在求解解集时会出现:x[ i ] * a[ i ][ i ] ≡ a[ i ][ COL ] (mod p),想要求 x[ i ] 就需要用到乘法逆元了。
另外该系数矩阵,可由范德蒙德行列式证明行列式大于 0,所以该 方程组必有唯一解。
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<math.h> #include<string.h> #define N 100 int p, COL, ROW; char s[N]; int a[N][N], x[N]; void show(void) { puts(""); for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL + 1; j++) { printf("%d ", a[i][j]); }puts(""); } } inline int gcd(int a, int b) { return b ? gcd(b, a%b) : a; } inline int lcm(int a, int b) { return a*b / gcd(a, b); } int qmul(int a, int b) { int res = 1; while (b) { if (b & 1) res = res*a%p; b >>= 1; a = (a%p)*(a%p) % p; } return res; } // 只有 唯一解 int Gauss() { int row, col; for (row = 0, col = 0; row < ROW&&col < COL; col++, row++) { int mr = row; for (int i = row + 1; i < ROW; i++) if (abs(a[i][col]) > abs(a[mr][col])) mr = i; if (mr != row) for (int i = col; i < COL + 1; i++) { int t = a[mr][i]; a[mr][i] = a[row][i]; a[row][i] = t; } for (int i = 0; i < ROW; i++) if (a[i][col] && i != row) { int LCM = lcm(abs(a[i][col]), abs(a[row][col])); int ta = LCM / a[i][col]; int tb = LCM / a[row][col]; if (a[i][col] * a[row][col] > 0) tb = -tb; for (int j = 0; j < COL + 1; j++) a[i][j] = ((a[i][j] * ta + a[row][j] * tb) % p + p) % p; // 加 p 是为了不变成负数 } } // show(); for (int i = row - 1; i >= 0; i--) { int t = a[i][COL]; x[i] = (t*qmul(a[i][i], p - 2)) % p; } return 0; } int main(void) { int t; scanf("%d", &t); while (t--) { scanf("%d %s", &p, s); COL = ROW = strlen(s); for (int i = 0; i < ROW; i++) { if (s[i] == '*') a[i][COL] = 0; else a[i][COL] = s[i] - 'a' + 1; for (int j = 0; j < COL; j++) a[i][j] = qmul(i + 1, j); } Gauss(); for (int i = 0; i < COL; i++) printf("%d ", x[i]); puts(""); } system("pause"); return 0; }
例题4:
Electric resistance(hdu 3976)
总体思路:利用 节点电压法 列线性方程,然后高斯消元法求解。
1,先普及一下知识:
节点:电路中三条或三条以上支路的交点。
参考点:任选的一个点,把该点作为电路的的电位参考点,通常选择为节点,因为会多出一个没用的节点。
节点电压:节点与参考点之间的电压
独立源:包含电压源和电流源。
电流源:电流不受外电路的影响而独立存在的电源。
电导:电阻的倒数。
自导:该节点所连的支路电导之和,如 G(11) 就是 1 号节点所连的各支路电导之和。
互导:相邻节点间公共电导之负值,如 G(1,2) 就是1 号节点和 2 号节点之间的电导之和的负值。
一般的,对于有 n 个节点的电路应用 KCL 列方程式时,只能写出 n-1 个独立方程,且为任意 n-1 个,这 n-1 个称为 独立节点,节点分析法可以从 KCL 推导证明(这里就不讲了)
所以我们用 节点分析法时,只需要用到 n-1 个节点
2,公式:
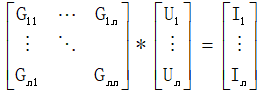
(注意这里的 n 为 结点数 - 1 )
对于第一个矩阵,主对角线上的元素为:自导;其余元素为:互导
对于第二个矩阵,其值为对应节点的节点电压。如 U1:1 号节点的节点电压
对于第三个矩阵,Ii 代表: 连接到第 i 个节点的各支路中独立源所引起的电流代数和
对于电流源产生的电流,当流入节点时为正,反之为负;
对于电压源产生的电流,当电压源正极靠近该节点时为正,反之为负。
3,具体思路
节点电压法就是通过电流和电阻求解电压,而这道题只给我们电阻,那么就需要我们自己外加电压源。为了计算方便,我们就在 节点1 和 节点 n 之间外加电流源,为什么是电流源呢?当然是为了容易求电流了。而且既然追求简单,我们自然要贯彻到底,就可以设电流源流出的电流为 1 。又因为只需要用到 n-1 个节点,所以可设 节点1 电压为 0。

展开得到(结点数-1)个方程 :
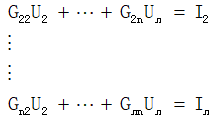
于是有增广矩阵:
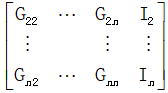
求解出 n 节点电压后,有:
(节点 n 的电压 - 0 (节点 1的电压)) / 1(节点1和节点n 之间的 总电流)== 等效电阻
化简一下就是:节点 n 的电压 == 等效电阻
注意点①:节点1 是不用求的,所以我们只用到 节点2 到 节点n。 而我的代码里的增广矩阵是从下标 0 开始的,所以各位要看清楚,a[0][0] 对应的是 G21,即 节点1 和 节点 2 之间电阻的倒数。
注意点②:各节点间只有 节点1 和 节点n 之间有独立电流源引起的电流,所以 U1 和 Un 为 1(当然,U1 没用到),其他皆为 0
4,该方程组唯一可解
① 目前不会证明。那你问我为什么知道唯一可解?我只能说因为代码用唯一可解的办法去写,去提交,过了,所以可以判断唯一可解。
② 值得一提的是,我在尝试证明并构造数据的过程中,发现
double b = 0;
printf("%.2lf\n", 1.0 / b);
这个的输出是:inf
③ 目前系数矩阵有三个特点,我列出来,可惜不会证明,也不知道这条件够不够证明。
1,对称矩阵
2,没有零元素(因为题目说: You may assume that any two nodes are connected!)
3,只有对角线是正数,其余都是负数,且对角线的绝对值是其所在行,也是其所在列的最大值。
5,代码
 View Code
View Code
============ =========== ========= ======== ======== ====== ====== ==== == =
宿新市徐公店 宋代: 杨万里



 浙公网安备 33010602011771号
浙公网安备 33010602011771号