数学建模线性规划例题分析

                                

分析：

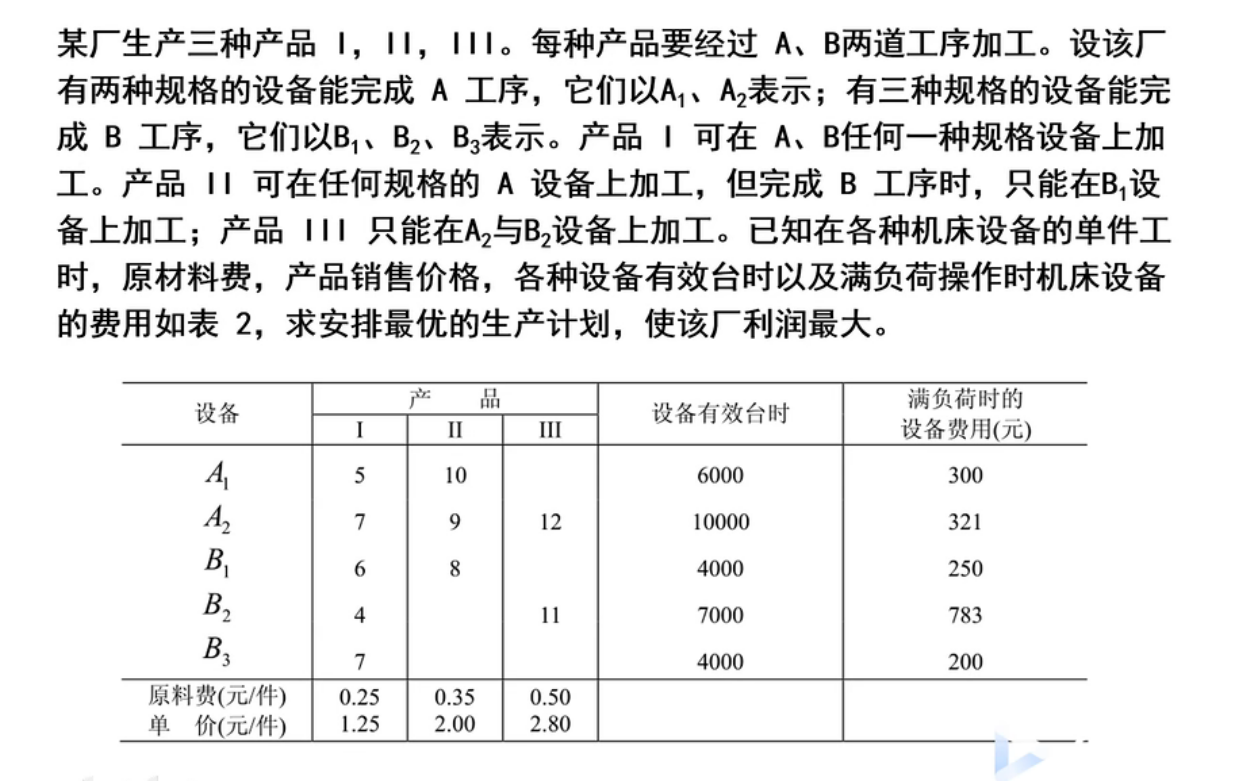
（1）、从题目中可知，I，II，III这三个产品都要经过A,B两道工序，其意思是无论是I还是II，亦或是III，都是依次通过A或B工序，从而得出了三个满足条件（设I产品中A₁、A₂、B₁、B₂、B₃的完成工序的产品个数为X1,X2,X3,X4,X5；II产品中A₁、A₂、B₁的完成工序的产品个数为X6,X7,X8；III产品中A₂、B₂的完成工序的产品个数为X9，X10）：【经过A和经过B的总个数相等】　　　　

X1+X2+X3=X4+X5;
X6+X7=X8;
X9=X10;

（2）、设备有效台时是指一个设备在工作时间内真正起到作用的时间（就好比如一个星期7天，3台设备每天工作8小时，但实际上真正有效的时间为4小时，所以设备有效台时=3*7*4=84台时；

满负荷时的设备费用（元）是指一台设备在有效台时的时候，总共所需要的费用；

从而引出

 　　　　　　　　　    单位时间内设备的费用=满负荷时的设备费用/设备有效台时；

（3）、单件价的利润=单价-原料费；

 

目标函数：

利润=【I或II或III单件价的利润】*【在A或B工序的I或II或III的总个数】-【A₁或A₂或B₁或B₂或B₃单位时间内设备的费用】*【A₁或A₂或B₁或B₂或B₃所有个数*单个个数所需花费时间（单件工时）】：

 Z = (1.25-0.25)*(X1+X2)+(2-0.35)*(X8)+(2.8-0.5)*(X9)-(300/6000)*(5*X1+10*X6)-(321/10000)*(7*X2+9*X7+12*X9)-(250/4000)*(6*X3+8*X8)-(783/7000)*(4*X4+11*X10)-(200/4000)*(7*X5);

约束条件：　　　　　　　　　　　　　　　　

 

5*X1+10*X5<=6000;
7*X2+9*X7+12*X9<=10000;
6*X3+8*X8<=4000;
4*X4+11*X10<=7000;
7*X5<=4000；
X1+X2+X3=X4+X5;
X6+X7=X8;
X9=X10;
Xi>=0(i=1,2,···,10);

 

　　

 

 

 

 

用Matlab来实现：

clc;clear;
c = [3/4,7753/10000,-3/8,-3132/7000,-7/20,-1/2,-2889/10000,1.15,19148/10000,-8613/7000];
A = [5,0,0,0,0,10,0,0,0,0;
     0,7,0,0,0,0,9,0,12,0;
     0,0,6,0,0,0,0,8,0,0;
     0,0,0,4,0,0,0,0,0,11;
     0,0,0,0,7,0,0,0,0,0];
 b = [6000;10000;4000;7000;4000];
 Aeq = [1,1,-1,-1,-1,0,0,0,0,0;
        0,0,0,0,0,1,1,-1,0,0;
        0,0,0,0,0,0,0,0,1,-1];
 beq = [0;0;0];
 lb = zeros(10,1);
 [x,y] = linprog(-c,A,b,Aeq,beq,lb,[]);
 fprintf('最优方案应该为:\n')
 for i = 1:10
     fprintf('x%d = %.5f\n',i,x(i));
 end
 fprintf('最大利润为%.5f元\n',-y);

 

 

实现结果：

Optimization terminated.
最优方案应该为:
x1 = 1200.00000
x2 = 230.04926
x3 = 0.00000
x4 = 858.62069
x5 = 571.42857
x6 = 0.00000
x7 = 500.00000
x8 = 500.00000
x9 = 324.13793
x10 = 324.13793
最大利润为1146.56650元