个人项目-----数独
(1)GitHub地址:https://github.com/as5290/sudoku
(2)
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
|
|
|
· Estimate |
· 估计这个任务需要多少时间 |
10 |
|
|
Development |
开发 |
|
|
|
· Analysis |
· 需求分析 (包括学习新技术) |
600 |
|
|
· Design Spec |
· 生成设计文档 |
120 |
|
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
0 |
|
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
120 |
|
|
· Design |
· 具体设计 |
60 |
|
|
· Coding |
· 具体编码 |
120 |
|
|
· Code Review |
· 代码复审 |
30 |
|
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
180 |
|
|
Reporting |
报告 |
|
|
|
· Test Report |
· 测试报告 |
60 |
|
|
· Size Measurement |
· 计算工作量 |
30 |
|
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 |
|
|
|
合计 |
1360 |
|
(3)
在老师刚刚布置了这个个人项目时,我是感觉很难受的,毕竟自己数独都玩不溜还要写个解数独的程序。加上也没有过开发项目的经验,所以刚拿到题目时是毫无头绪的。
我想了想可能用到的算法,我想到的是回溯算法,又想了想整个代码的结构,然后上百度查了查相关资料,包括数独的算法之类的。我选择参考的方法都是比较接近我的想法的方法,帮助自己捋清思路。思路清晰后便开始敲代码。
(4)设计过程:
我的程序分为三个函数:jie()、Get_num()、create()。
三个函数关系如下:
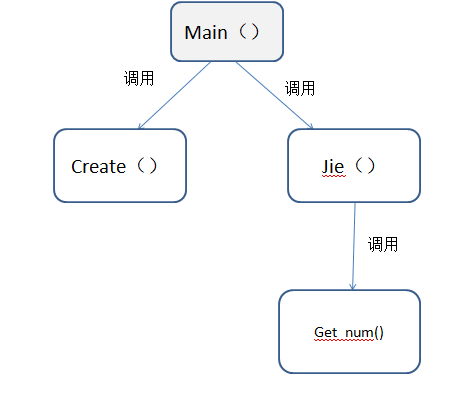
关键函数的流程图:
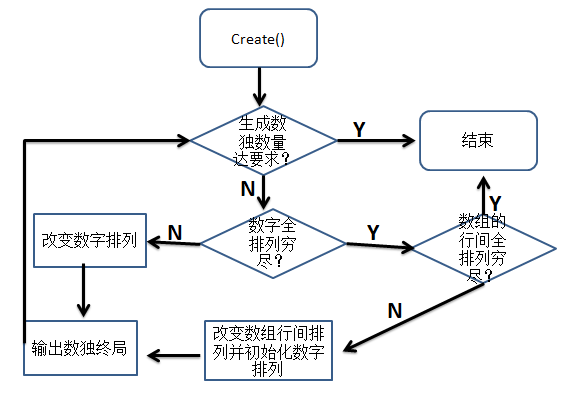
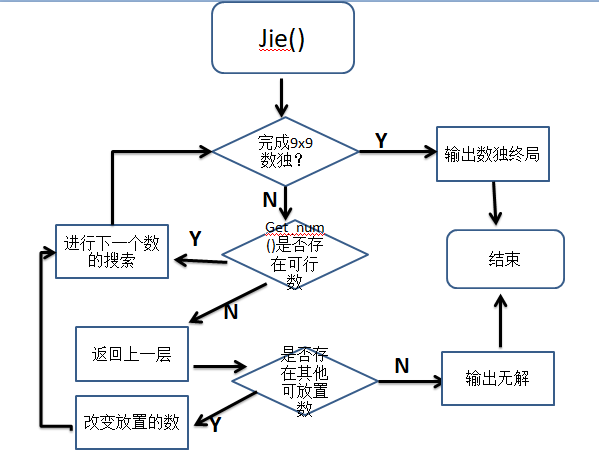
单元测试就设计对应的用例:测试create()函数时,测试用例:-c 10000等用例,以及-c abc这类错误的输入。
测试jie()时,测试用例:-s 输入文件路径。
(5)一开始我的程序生成1000000个数独终局时花了大约17秒时间,create是消耗最大的函数,create函数里主要是输出,然后发现printf的输出比较费时间,所以改成了putchar()输出。优化之后完成1000000个终局输出只需要不到5秒的时间。以下是优化后的性能分析:
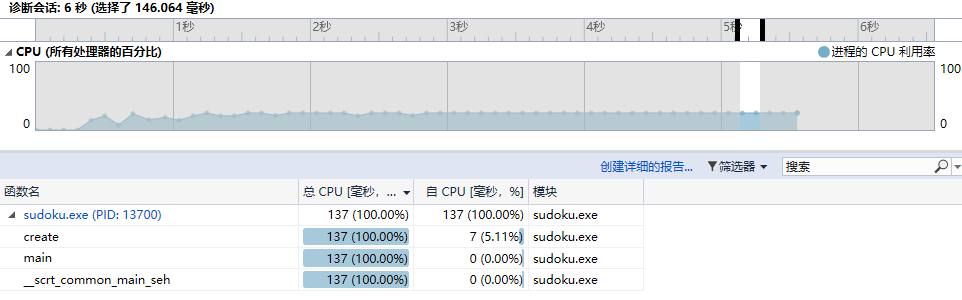
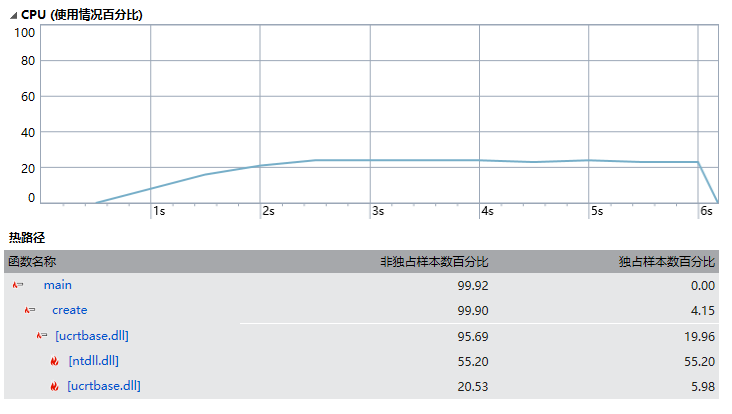
占用时间最多的是create函数。
void create(int n)
{
int times = 0;
int move[10] = { 0, 0, 3, 6, 1, 4, 7, 2, 5, 8 },
lie;
char N[10]={'9','1','2','3','4','5','6','7','8','9'};
if ( times < n )
{
for (int a = 0; a < 6; a++)
{
if (times == n)break;
if (a)
next_permutation(move + 4, move + 6);
for (int b = 0; b < 6; b++)
{
if (b)
next_permutation(move + 7, move + 9);
int t = 0; char kong = ' ';
do
{
if (t)
next_permutation(N + 2, N + 9);
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
if (j - move[i] < 0)lie = j - move[i] + 9;
else lie = j - move[i];
putchar(N[lie % 9]);
if (j < 9) putchar(kong);
}putchar('\n');
}
times++; t++;
if (times == n)break;
else putchar('\n');
}while (t<40320);
if (times == n)break;
}
}
}
}
(6)生成函数create()代码如上。我的思路是将每一个数独看成数独第一行从第二行开始,分别右移3、6、1、4、7、2、5、8列的结果。因为第一个已经固定,所以后面八个数的全排列8!=40320种终局,40320<10000000,不满足要求。所以考虑对于任何一个数独终局的1~3行、4~6行和7~9行,任意交换这三行的顺序,得到的仍然是一个合法的终局,而只需加上4~6行和7~9行的全排列就超过了要求的1000000种不同终局。
int Get_Num(int hang, int lie)
{
if (hang > 9 || lie > 9) return 1;
if (v[hang][lie])
{
if (lie < 9)
{
if (Get_Num(hang, lie + 1))
return 1;
}
else
{
if (hang < 9)
{
if (Get_Num(hang + 1, 1))
return 1;
}
else return 1;
}
}
else
{
for (int num = 1; num <= 9; num++)
{
int can = 1;
for (int i = 1; i <= 9; i++)
{
if (Initial_Num[i][lie] == num)
{
can = 0;
break;
}
}//列是否有该数
if (can)
{
for (int j = 1; j <= 9; j++)
{
if (Initial_Num[hang][j] == num)
{
can = 0;
break;
}
}
}//行是否有该数
if (can)
{
int max_hang, max_lie;
if (hang % 3 == 0)
max_hang = hang;
else
max_hang = (hang / 3) * 3 + 3;
if (lie % 3 == 0)
max_lie = lie;
else
max_lie = (lie / 3) * 3 + 3;
for (int i = max_hang - 2; i <= max_hang; i++)
{
for (int j = max_lie - 2; j <= max_lie; j++)
{
if (Initial_Num[i][j] == num)
{
can = 0;
break;
}
}
if (!can) break;
}
}//3x3格子里是否有该数
if (can)
{
Initial_Num[hang][lie] = num;
if (lie < 9)
{
if (Get_Num(hang, lie + 1))
return 1;
}
else
{
if (hang < 9)
{
if (Get_Num(hang + 1, 1))
return 1;
}
else return 1;
}
Initial_Num[hang][lie] = 0;
}
}//1--9是否可以放置
}
return 0;
}
这是解数独用到的关键的代码。主要思路是找出每个位置可以放置的数,然后搜下一个位置,如果下一个位置没有可以放置的数就回溯返回上一层,查找上一层是否还可以放置另外的数,直到找完9X9个格子得到解。
(7)
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
|
|
|
· Estimate |
· 估计这个任务需要多少时间 |
|
10 |
|
Development |
开发 |
|
|
|
· Analysis |
· 需求分析 (包括学习新技术) |
|
500 |
|
· Design Spec |
· 生成设计文档 |
|
100 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
|
0 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
|
150 |
|
· Design |
· 具体设计 |
|
80 |
|
· Coding |
· 具体编码 |
|
180 |
|
· Code Review |
· 代码复审 |
|
30 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
|
240 |
|
Reporting |
报告 |
|
|
|
· Test Report |
· 测试报告 |
|
100 |
|
· Size Measurement |
· 计算工作量 |
|
30 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
|
30 |
|
|
合计 |
|
1450 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号