Swust OJ982: 输出利用二叉树存储的普通树的度

题目描述

普通树可转换成相应的二叉树（该二叉树的根结点一定缺少右儿子），反之亦然。故而可以根据相应的转换方法去统计某一二叉树对应的普通树的度。普通树的度为其结点儿子数的最大值。 输出利用二叉树存储的普通树的度.

输入

输入为接受键盘输入的由大写英文字符和"#"字符构成的一个字符串（用于创建对应的二叉树）。

输出

若表示的二叉树对应普通树，则该普通树的度；否则输出ERROR。

样例输入复制

AB#CD##E###

样例输出复制

3
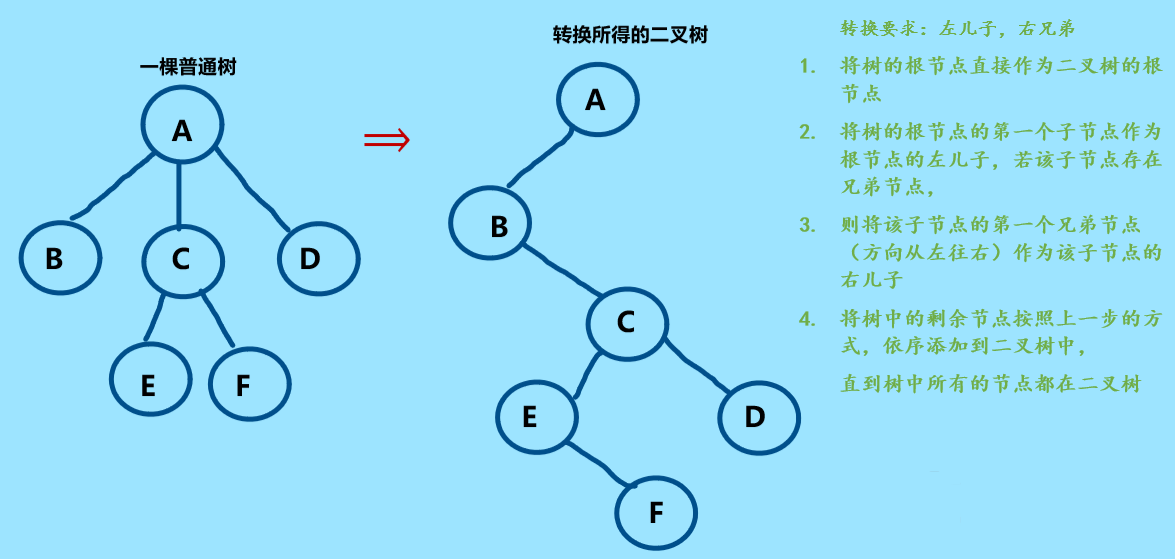
知识点：普通树转换为二叉树

上图树的度即为3.

所以计算普通树的度——树的所有结点的度的最大值作为这棵树的度

 

故对于二叉树，计算出同一直线上的右结点的最大值即为普通树的度

算法：

 void Degree(Tree *&t,int n)
 {
     if(t!=NULL)
     {
         Degree(t->rchild,n+1);
         Degree(t->lchild,1);
     }
     if(max<n)
         max=n;
 }

完整代码：

#include<iostream>
#include<stdlib.h>
#include<stdio.h>
using namespace std;
int max=0;//Global variables
typedef struct node
{
    char data;
    struct node *lchild,*rchild;
 }Tree;
//先序遍历递归创建二叉树
 void CreateTree(Tree *&t)
 {
     char ch;
     cin>>ch;
     if(ch!='#')
     {
         t=(Tree*)malloc(sizeof(Tree));
         t->data=ch;
         CreateTree(t->lchild);
         CreateTree(t->rchild);
     }
     else
     t=NULL;    
 }
 //计算二叉树存储的普通树的度
 void Degree(Tree *&t,int n)
 {
     if(t!=NULL)
     {
         Degree(t->rchild,n+1);
         Degree(t->lchild,1);
     }
     if(max<n)
         max=n;
 }

 int main()
 {
     Tree *t;
     CreateTree(t);
     int n=0;
     if(t->rchild==NULL)
     {
         Degree(t,n);
         cout<<max-1;
     }
     else
     cout<<"ERROR";
     return 0;
 }