图论学习笔记~
八月集训图论学习笔记
1.同余最短路
同余最短路用来解决这样一类问题:
对于一个范围 $ [l,r] $ 找出其中有多少个重量可以被如干个物品通过非负次数的线性组合得出。
(即:区间完全背包问题)
形式化地,给出 \(n\) \((1\le n \le 15)\)个物品 \({a_i}\) (\(1 \le a_i \le 10^5\)) 对于指定的区间 \([l,r]\) (\(1\le l,r \le 10^{15}\) ),找出其中能够被写成 \(\sum\limits_{c_i\ge 0}a_ic_i\) 的个数。
显然可以观察到一个结论,如果对于一个数 \(p\) 有解,那么对于任意的数 \(p+ca_i\) 也显然有解。
考虑任意一个 \(a_i\) 的同余类 \(M_{i,j}\) 只需找出最小可以表示的数 \(dp_{i,j}\) ,那么有
不妨设 \(a_1\) 是最小值,考虑处理 \(dp_1\) ,对于\(dp_i(2 \le i \le n)\)
具体做法考虑 \(SPFA\) 或者 \(dijkstra\) 算法。
时间复杂度分析:,
- \(SPFA\) :\(O(na_1k)\)
- \(Dijkstra\): \(O(na_1\log na_1)\)
毕竟少个 \(\log\) ,\(SPFA\) 快的飞起。
模板题:
墨墨的等式
不需要单独建图,直接在\(SPFA\) 中跑就可以了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int a[20];
queue<int> q;
bool vis[500010];
int d[500010];
int solve(int x){
int ans=0;
for(int i=0;i<a[1];i++){
if(x>=d[i]){
ans+=(x-d[i])/a[1]+1;
}
}
return ans;
}
signed main(){
int n,l,r;
cin>>n>>l>>r;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
memset(d,0x3f,sizeof d);
q.push(0);
d[0]=0;
vis[0]=1;
while(!q.empty()){
int v=q.front();
q.pop();
vis[v]=0;
for(int i=2;i<=n;i++){
int u=(v+a[i])%a[1];
if(d[v]+a[i]<d[u]){
d[u]=d[v]+a[i];
if(!vis[u]) {
vis[u]=1;
q.push(u);
}
}
}
}
cout<<solve(r)-solve(l-1);
}
[AT3621 [ARC084B] Small Multiple(2.00S/1024MB)]([AT3621 ARC084B] Small Multiple - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
远超 \(ARCtest-B\) 难度的题目。
题目大意:给定一个整数 \(K\) ,求一个整数 \(S\) 满足 \(K|S\) ,求出 \(S\) 个位数字之和的最小值并输出。
\(2\le k \le 10^5\)
\(Test-Input1\)
\(input\) : 6
\(output\) :3
显然。\(6 \times 2 =12\) 。
\(d_i\) 表示 \(x \bmod k =i\) 的数各位数字之和的最小值。
最终状态即 \(d_0\) 。
考虑连边。所有数字都可以从 1 通过 \(+1 和 \times 10 得到。\)
因此从每个点 \(i (0\le i < k)\) 连边。
#include<bits/stdc++.h>
#define int long long
using namespace std;
queue<int> q;
bool vis[500010];
int d[500010];
signed main(){
int k;
cin>>k;
memset(d,0x3f,sizeof d);
q.push(1);
d[1]=1;
vis[1]=1;
while(!q.empty()){
int v=q.front();
q.pop();
vis[v]=0;
int u=(v+1)%k;
if(d[v]+1<d[u]){
d[u]=d[v]+1;
if(!vis[u]) {
vis[u]=1;
q.push(u);
}
}
u=v*10%k;
if(d[v]<d[u]){
d[u]=d[v];
if(!vis[u]) {
vis[u]=1;
q.push(u);
}
}
}
cout<<d[0];
return 0;
}
2.广义圆方树
前言:MnZn太菜了,没有学过圆方树,只学过广义圆方树,两者具体区别可以看看其他的博客。
p.s.下文中圆方树均指广义圆方树。
广义圆方树是一种定义在无向图上的树形结构。
具体操作就是将一个无向图中每一个点双建一个方点,向该点双中所有点建边。原图中的点就是“圆点”。
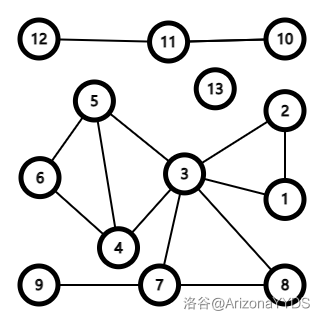
上面就是一个随便画的无向图。
它建立的圆方树长这样:
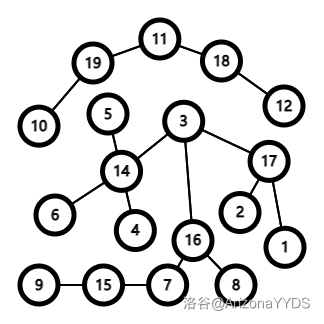
其中编号\(1-13\) 的是原图中的点,\(14-19\) 是新建立的点,即方点。
圆方树具有以下的\(Lemma\) (部分无证明我不会证):
\(Lemma\) \(\alpha\)
圆点 \(u\) 的度数等于在原图中它位于的点双个数。
\(Lemma\) $ \beta$
圆方树的每一条边都是从圆点连向方点。
\(Lemma\) \(\gamma\)
圆点是叶子节点 \(\iff\) 圆点不是割点。
Proof:(Lemma \(\gamma\) )
\(Case 1\) 若圆点 \(u\) 是割点,则它位于至少两个点双,故度数大于 1。
\(Case 2\) 若圆点\(u\) 不是割点。则它一定只能位于一个点双中。度数为1。
\(Lemma\) \(\delta\)
$(x,y) $ 在圆方树上的简单路径上进过的圆点就是在原图上的必经点。
比较复杂,请读者自己给出证明。
\(Lemma\) \(\epsilon\)
在圆方树上删除结点 \(u\) 之后圆方树的连通性与原图连通性相同。
Proof:(Lemma \(\epsilon\) )
\(Case 1\) 若圆点 \(u\) 不是割点,显然。
\(Case 2\) 若圆点\(u\) 是割点。考虑任意两个点 \(v,w\) 。
\(1^\circ\) \(v,w\) 属于一个点双。则原图中两点联通,圆方树上两点通过方点联通。
\(2^\circ\) \(v,w\) 属于不通点双。也很显然。
\(QED\)
</details>
<summary>blocktree</summary>
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node{
int v,next;
}e[400110];
vector<int> g[400010]; //block-tree
int p[200010];
int low[2000010],dep[2000010];
int w[4000010];
int cnt;
int sr; //square.size();
void add(int u,int v){
e[++cnt].v=v;
e[cnt].next=p[u];
p[u]=cnt;
}
int ans;
int tot;
int idx;
int top;
int st[2000010];
void dfs(int u,int fa){
sr++;
st[++top]=u;
low[u]=dep[u]=++idx;
w[u]=-1;
for(int i=p[u];i!=-1;i=e[i].next){
int v=e[i].v;
if(v==fa) continue;
if(dep[v]==0){
dfs(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dep[u]){
tot++;
g[tot].push_back(u);
g[u].push_back(tot);
w[tot]++;
do{
g[tot].push_back(st[top]);
g[st[top]].push_back(tot);
w[tot]++;
}while(st[top--]!=v);
}
}else{
low[u]=min(low[u],dep[v]);
}
}
}
int n,m;
signed main(){
cin>>n>>m;
tot=n;
for(int i=1;i<=100000;i++) p[i]=-1;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
for(int i=1;i<=n;i++){
if(dep[i]==0){
sr=0;
dfs(i,i);
top--;
}
}
for(int i=1;i<=tot;i++){
for(int j=0;j<g[i].size();j++){
cout<<i<<" "<<g[i][j]<<endl;
}
}
return 0;
}
</details>
圆方树实现代码。\(Tarjan\) 算法。板子非常好写(比 \(2-SAT\)好写)
ZJOI2004嗅探器
正解\(Tarjan\) ,但我就是要用圆方树分析图。
这种题圆方树方便多了~
一句话题意:在一个无向图上给两个点 \(x,y\) ,找出它们必经路线经过的割点最小编号。
找出圆方树上找圆点。
</details>
<summary>blocktree</summary>
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node{
int v,next;
}e[1000110];
vector<int> g[2000010]; //block-tree
int p[1000010];
int low[1000010],dep[6000010];
int w[1000010];
int cnt;
int sr; //square.size();
void add(int u,int v){
e[++cnt].v=v;
e[cnt].next=p[u];
p[u]=cnt;
}
int ans;
int tot;
int idx;
int top;
int st[1000010];
void dfs(int u,int fa){
st[++top]=u;
low[u]=dep[u]=++idx;
for(int i=p[u];i!=-1;i=e[i].next){
int v=e[i].v;
if(v==fa) continue;
if(dep[v]==0){
dfs(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dep[u]){
tot++;
g[tot].push_back(u);
g[u].push_back(tot);
w[tot]++;
do{
g[tot].push_back(st[top]);
g[st[top]].push_back(tot);
}while(st[top--]!=v);
}
}else{
low[u]=min(low[u],dep[v]);
}
}
}
int n,m;
bool tg;
void dfs2(int u,int fa,int ans,int ed,int stl){
if(tg==1) return;
if(u==ed){
if(ans==0){
cout<<"No solution"<<endl;
tg=1;
exit(0);
}else{
cout<<ans;
tg=1;
exit(0);
}
}
if(u!=stl&&g[u].size()>1&&u<=n) ans=(ans==0?u:min(ans,u));
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(v==fa) continue;
dfs2(v,u,ans,ed,stl);
}
}
signed main(){
cin>>n;
tot=n;
for(int i=1;i<=1000000;i++) p[i]=-1;
for(int i=1;i<=500000;i++){
int x,y;
scanf("%lld%lld",&x,&y);
if(x==0||y==0){
break;
}
add(x,y);
add(y,x);
}
int start,end;
scanf("%lld%lld",&start,&end);
dfs(start,0);
if(!dep[end]){
cout<<"No solution"<<endl;
return 0;
}
dfs2(start,0,0,end,start);
return 0;
}
</details>


 浙公网安备 33010602011771号
浙公网安备 33010602011771号