线段树

【线段树的定义】

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。^①

 

【线段树的分解】

 

 

 

 

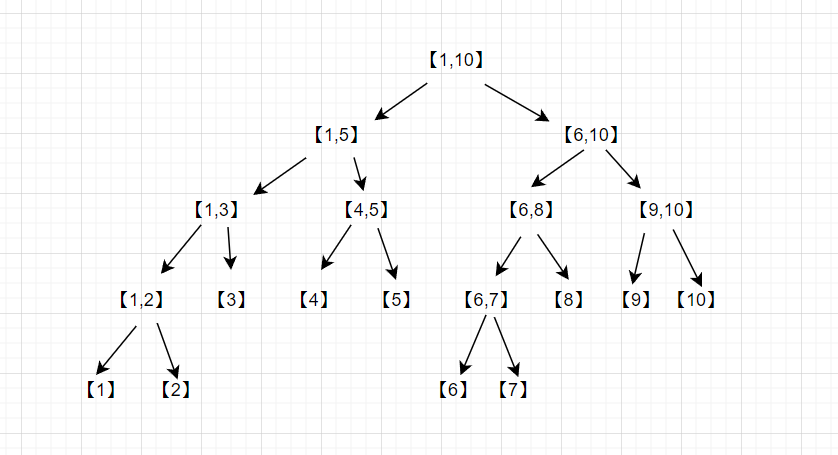
线段树的优势在哪里呢？

1.连续区间求累加和

若我想求区间【2,7】的累加和，正常累加需要从元素2累加到元素7，需要做6次加法。但利用线段树，我们可以拼凑出一个区间得出累加和，且使其累加次数减少。

如上图，我可以将【2】，【3】，【4,5】，【6,7】区间拼成，需要做四次累加，这样就可以达到减少累加次数的目的。

 

2.便于修改

如果只是求连续区间的累加和的话，可以求出第k项的累加和S_k,（S_k = S₁+S₂……S_K），这样对于一个区间只需做一次减法即可求出累加和。（对于【a,b】累加和等于Sb - Sa）。

但这种方法的坏处就在于当我修改树上的值时，我需要将这个元素后所有的累加和都更新。这时耗时将会大大增加。而利用线段树，我只需更新一个区间沿路树节点的值，耗时会小很多。

 

 

【参考资料】

1. 线段树定义. 百度百科: https://baike.baidu.com/item/%E7%BA%BF%E6%AE%B5%E6%A0%91/10983506?fr=aladdin

2. 线段树原理.  岩之痕 https://blog.csdn.net/zearot/article/details/52280189