python算法:杨辉三角

一，认识递归函数

1，什么是递归?
递归的工作原理是，如果函数需要处理的问题大小合适，则直接求解并返回结果，
否则将问题分解成两个或多个更小的子问题，并对子问题进行相同的处理，
直到问题无法分解为止

2,什么是递归函数:
递归函数（recursive function）是指在函数体中可以调用自己的函数

3,语法

def fn():
    # ...
    if condition:
        # 停止自我调用
    else:
        fn()
    # ...

4,递归函数的优点和缺点

递归函数的优点:它们可以帮助程序员在处理复杂问题时提供一种简单且易懂的解决方案。
递归函数使代码具有可读性和可重用性，
而且可以使用递归函数解决使用其他方法难以处理的问题。
递归函数的缺点: 递归函数可能会在运行时占用较多的系统资源，
因为它们需要在堆栈上存储多个函数调用
其次，递归函数可能导致代码变得不容易理解，
因为它具有一定的复杂度

二，杨辉三角的题目与解析

1,题目：

杨辉三角，也称为帕斯卡三角，是一个以数字排列而成的三角形图案。每个数字是其左上方和右上方数字之和，首行为1

如图:

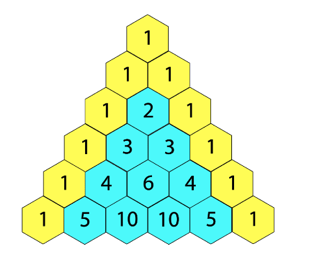
2，思路:

第 x 行有 x 个值（设起始行为第1行）。

对于第 x 行的第 y（y>=3）个值，有：当 y=1 或 y=x 时，其值为 1；当 y!=1 且 y!=x 时，其值为第 x-1 行的第 y-1 个值与第 x-1 行的第 y 个值之和。

可得到如下规则:

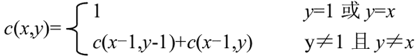
说明：刘宏缔的架构森林—专注it技术的博客，
网址：https://imgtouch.com
本文: https://blog.imgtouch.com/index.php/2024/03/15/python-suan-fa-yang-hui-san-jiao/
代码: https://github.com/liuhongdi/ 或 https://gitee.com/liuhongdi
说明：作者:刘宏缔邮箱: 371125307@qq.com

三，代码实现

1,用递归函数实现

# x: 行
# y: 列
def triangles(x, y):
    # y=1或y=x时，函数返回值为1
    if y == 1 or y == x:
        return 1
    else:
        # y为其他值时,等于 上一行的y-1列加上一行的y列的和
        z = triangles(x - 1, y - 1) + triangles(x - 1, y)
        return z
 
n = int(input("请输入杨辉三角的行数："))
for i in range(1, n + 1):  # 输出n行
    line = ''        # 保存当前行
    for j in range(1, i + 1):
        # 调用递归函数，得到第i行的第j个值
        value = triangles(i, j)
        line += '  '+str(value)
    print(line.center(50))

运行结果:

请输入杨辉三角的行数：11
                         1                        
                        1  1                      
                      1  2  1                     
                     1  3  3  1                   
                   1  4  6  4  1                  
                 1  5  10  10  5  1               
               1  6  15  20  15  6  1             
             1  7  21  35  35  21  7  1           
           1  8  28  56  70  56  28  8  1         
        1  9  36  84  126  126  84  36  9  1      
   1  10  45  120  210  252  210  120  45  10  1

2,for循环实现

# x: 需要生成的杨辉三角的总行数
def triangle_1(x):
    triangle = [[1], [1, 1]]  # 初始化杨辉三角前两行
    for n in range(3, x+1):  # 从第三行开始添加
        for i in range(0, n - 1):      # 每行中逐列添加
            if i == 0:    # 第0列，添加当前行列表[1,1]
                triangle.append([1, 1])
            else:
                # 求上一行的第i-1个和第i个的和,并插入当前行列表中
                dst = triangle[n - 2][i] + triangle[n - 2][i - 1]
                # 插入到当前行
                triangle[n - 1].insert(i, dst)
    return triangle
 
x = 11
triangle = triangle_1(x)
# 遍历结果，逐行打印
for i in range(x):
    print(str(triangle[i]).center(50))  # 转为str,居中显示

运行结果:

                       [1]                        
                      [1, 1]                      
                    [1, 2, 1]                     
                   [1, 3, 3, 1]                   
                 [1, 4, 6, 4, 1]                  
               [1, 5, 10, 10, 5, 1]               
             [1, 6, 15, 20, 15, 6, 1]             
           [1, 7, 21, 35, 35, 21, 7, 1]           
         [1, 8, 28, 56, 70, 56, 28, 8, 1]         
      [1, 9, 36, 84, 126, 126, 84, 36, 9, 1]      
 [1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]

一，认识递归函数

二，杨辉三角的题目与解析

三，代码实现

公告