python算法:n皇后

一，认识递归函数

1，什么是递归?
递归的工作原理是，如果函数需要处理的问题大小合适，则直接求解并返回结果，
否则将问题分解成两个或多个更小的子问题，并对子问题进行相同的处理，
直到问题无法分解为止

2,什么是递归函数:
递归函数（recursive function）是指在函数体中可以调用自己的函数

3,语法

def fn():
    # ...
    if condition:
        # 停止自我调用
    else:
        fn()
    # ...

4,递归函数的优点和缺点

递归函数的优点:它们可以帮助程序员在处理复杂问题时提供一种简单且易懂的解决方案。
递归函数使代码具有可读性和可重用性，
而且可以使用递归函数解决使用其他方法难以处理的问题。
递归函数的缺点: 递归函数可能会在运行时占用较多的系统资源，
因为它们需要在堆栈上存储多个函数调用
其次，递归函数可能导致代码变得不容易理解，
因为它具有一定的复杂度

二，DFS

1,深度优先遍历(Depth First Search, 简称 DFS):
主要思路是从图中一个未访问的顶点开始，沿着一条路一直走到底，
然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底……
不断递归重复此过程，直到所有的顶点都遍历完成，
它的特点是一定要先走完一条路，再换一条路继续走

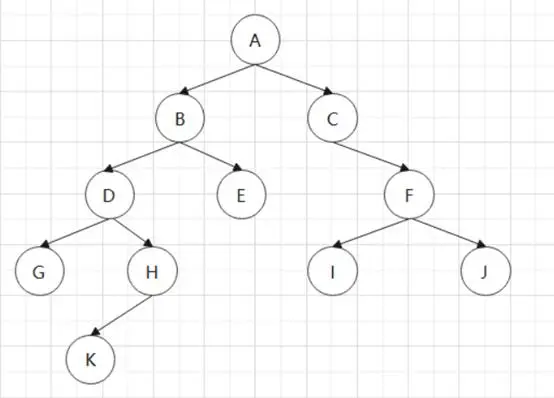
2，二叉树的前序遍历用的就深度优先遍历，如下图
二叉树前序遍历的结果为：ABDGHKECFIJ：

三,n皇后问题与解决思路

1,八皇后问题（英文：Eight queens），由国际象棋棋手马克斯·贝瑟尔提出，是回溯算法的典型案例。
问题为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

2, N皇后问题是对八皇后的扩展:它研究的是将 n 个皇后放置在一个 n×n 的棋盘上，使皇后彼此之间不相互攻击。

3, 解析:
以四个皇后为例，研究皇后在棋盘上的放法,如图:

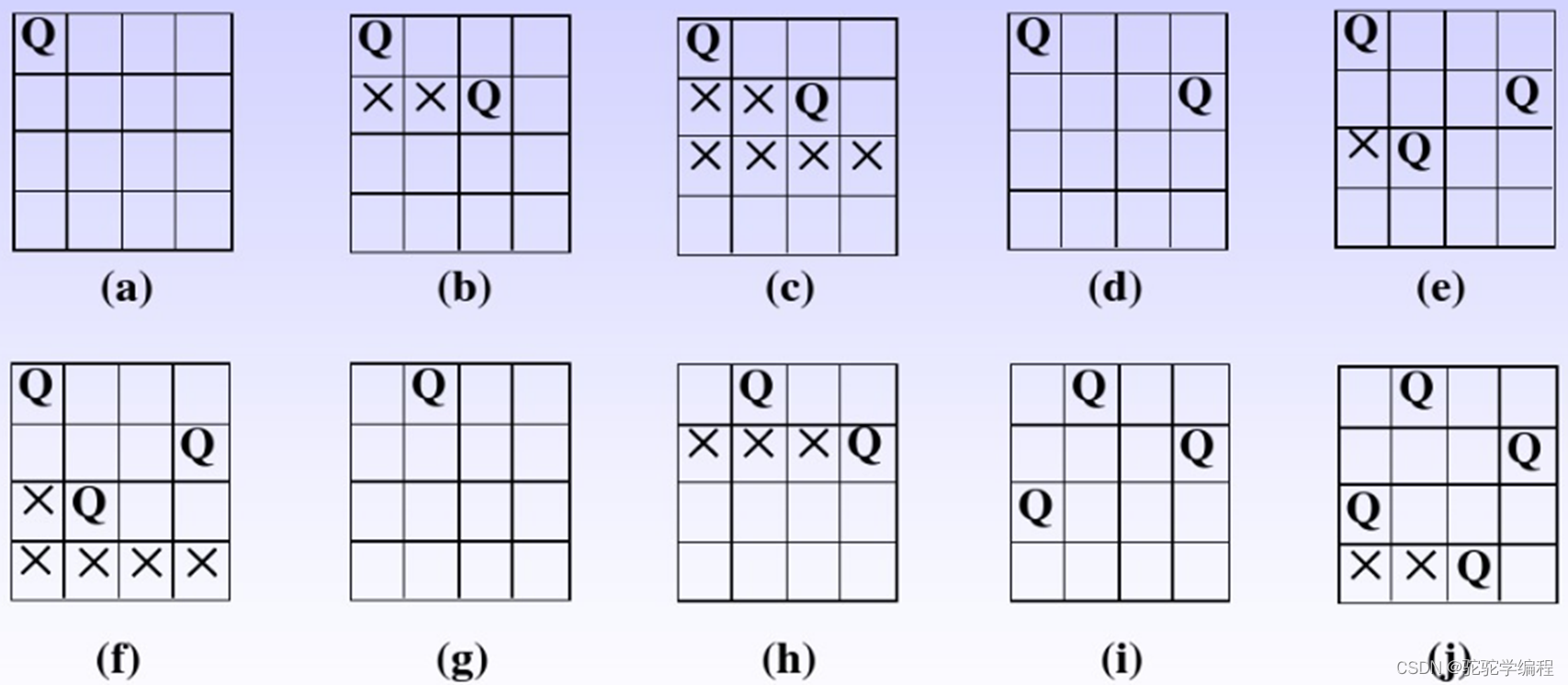
先将第一个皇后放在第一行的第一列上，符合题目要求

开始放置第二个皇后。放在第二行的第一个与第一行的皇后为同一列，不符合题意，继续向后搜素，放在第二列上面与第一个皇后在同一斜线上，不符合题意，继续向后搜素，发现放在第三列符合题意

开始放置第三个皇后。放在第三行的任意位置都会出现冲突，此时需要回溯，将第二个皇后放置在第四列，此时符合题意，继续放置第三个皇后，发现第三个皇后放置在第三行的第二列符合题意

继续放置第四个皇后。放在第四行的任意位置都会出现冲突，此时需要回溯，第三个皇后向后移动，发现依然不符合题意，继续回溯，第二行的皇后无法再向后移动，继续回溯，将第一个皇后向后移动到第二列，符合题意

移动第二个皇后，发现放在第四列符合题意

移动第三个皇后，发现放在第一列符合题意

移动第四个皇后，发现放在第三列符合题意

回溯结束

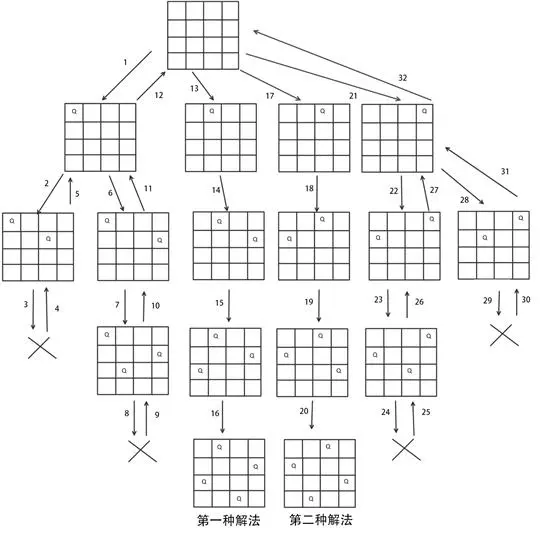
4,以四皇后为例的遍历解析,
从第0行开始，遍历每一列的位置，
如果可以摆放，则摆放，并跳到下一行继续
如果不可以摆放，则回退到上：

说明：刘宏缔的架构森林—专注it技术的博客，
网址：https://imgtouch.com
本文: https://blog.imgtouch.com/index.php/2024/03/11/python-suan-fa-n-huang-hou/
代码: https://github.com/liuhongdi/ 或 https://gitee.com/liuhongdi
说明：作者:刘宏缔邮箱: 371125307@qq.com

四，代码

# 判断是否可以放置皇后
# col: 当前列
# res: 位置总结果
# row: 当前行
def is_ok(col, res, row):
    # 遍历已经放好皇后的所有行
    # 无需判断是否在同一行，因为一行有值后，会进行到下一个 dfs
    for i in range(row):
        # 1、是否在同一列中
        # 2、左斜线：（行 + 列）的值相等
        # 3、右斜线：（列 - 行）的值相等
        if res[i] == col or res[i] + i == row + col or res[i] - i == col - row:
            return False
    return True
 
 
# 递归遍历棋盘的每一格，从第0行开始，遍历每行的每一列
# 参数：皇后总数  位置总结果  当前放置第几行
# Depth-First Search，也就是DFS算法，深度优先算法
# DFS一般可以用来遍历或者搜索树或图
def dfs(count, res, row):
    # 如果当前行数 = 皇后总数，
    # 说明已经遍历过了最后一行，即最后一行已成功放入了皇后
    # 结束跳出
    if row == count:
        print("结果:", res)
        return
    # 遍历 row 行中的每一列
    for col in range(count):
        # 判断当前列是否可放置皇后
        if is_ok(col, res, row):
            # 将该 row 行的数值改成列数 col
            res[row] = col
            # 进行下一行的搜索
            dfs(count, res, row + 1)
 
 
# count: 皇后的数量
count = int(input('请输入皇后的数量：'))
 
# 最终皇后的位置 （下标：第几行 数值：第几列）
res = [0 for _ in range(count)]
 
# 从第一行开始
row = 0
 
# 参数：皇后总数  位置结果  当前放置第几行
dfs(count, res, row)

运行结果:

请输入皇后的数量：4
结果: [1, 3, 0, 2]
结果: [2, 0, 3, 1]

一，认识递归函数

二，DFS

三,n皇后问题与解决思路

四，代码

公告