单调栈

单调栈问题

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

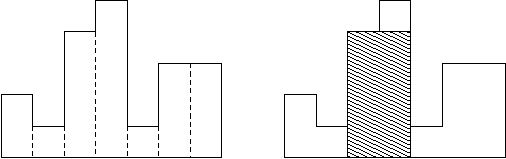
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式
输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式
对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围
1≤n≤100000,
0≤hi≤1000000000
输入样例：
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例：
8
4000

	#include<iostream>
	#include<algorithm>
	#include<stdio.h>
	using namespace std;
	const int N=100010;
	int q[N];
	int n;
	int l[N],r[N],h[N];
	typedef long long ll;
	void get(int bound[N])//找到第一个高度小于当前位置高度的下标，储存在l数组里，在将原来的高度数组翻转，找到第一个高度小于当前位置高度的下标。
	{
	    int tt=0;
	    h[0]=-1;
	    for(int i=1;i<=n;i++)
	   { while(h[q[tt]]>=h[i])//栈顶高度大于我当前的高度，就删掉
	        tt--;
	       bound[i]=q[tt];剩下的元素就是左边第一个比我小的元素
	      q[++tt]=i;将当前的元素加到栈里面去
	   }
	}
	int main(){
	    
	    while(cin>>n,n)
	    {
	        for(int i=1;i<=n;i++)
	        {
	            cin>>h[i];
	        }
	        get(l);
	       reverse(h+1,h+n+1);
	       get(r);
	       ll res=0;
	       for(int i=1,j=n;i<=n;j--,i++)
	       {
	           res=max(res,h[i]*(n+1-l[j]-r[i]-1ll));  
        //为什么是n+1-l[j]-r[i]-1ll,因为翻转以后，h数组也翻转了，是从后往前开始
	       }
	        cout<<res<<endl;
	    }
	}