绵阳2020CCPC补题
绵阳2020CCPC D,K,J,L,G
D. Defuse the Bombs
知识点:二分答案
复杂度:\(O(nlogn+log^2n)\)
vp时我猜了一个结论,验了几个样例就写了,喜提WA3
然后队友写了二分答案复杂度\(O(log^2n)\),也WA3
然后队友发现是二分边界错了,改了后AC
反思:这题WA的两发都是可以避免的,即没判断更多的样例,也没计算二分上界
先排序求一个前缀和
二分答案后进行判断当前答案 \(ans\)
在 a 数组中二分得到第一个比x小的位置
那么 \(ans\) 是否可行即比较 \(pre[i] + x\) 与 \(i*x\) 的大小
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;
const int N = 1e5 + 5;
int n;
int a[N];
ll pre[N];
bool check(ll x)
{
auto it = upper_bound(a + 1, a + n + 1, x) - a - 1;
return pre[it] + x >= it * x;
}
void solve()
{
cin >> n;
rep(i, 1, n) cin >> a[i];
sort(a + 1, a + n + 1);
rep(i, 1, n) pre[i] = pre[i - 1] + a[i];
ll l = 0, r = 2e9 + 10, mid;
while (l < r)
{
mid = (l + r + 1) >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
cout << l + 1 << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
K. Knowledge is Power
知识点:构造
复杂度:\(O(1)\)
该题思路出的很快,并且也排除了几个错误情况,但是还是没有完全验证正确性,导致WA一发,耐下心来这一发也可以避免的
一点点失误累积可能就会成为下次名落孙山的原因了
明显当 n 为奇数时可以拆成 \(\frac{n-1}{2}\) 与 \(\frac{n+1}{2}\)
当 n 为偶数时,我们讨论 \(\frac{n}{2}\) 的奇偶
- 当 \(\frac{n}{2}\) 为偶数时
显然可以拆成 \(\frac{n}{2}-1\) 与 \(\frac{n}{2}+1\) - 当 \(\frac{n}{2}\) 为奇数时
拆成 \(\frac{n}{2}-2\) 与 \(\frac{n}{2}+2\) 显然是一种合法情况
所以该情况答案的上界就为 4
样例贴心的给出了反例,什么良心出题人
此时显然 n 不可能拆成多于 3 个数
而 n 拆成 3 个数的情况显然固定- n % 3 == 0
n 可以拆成 \(\frac{n}{3}-1\) , \(\frac{n}{3}\) , \(\frac{n}{3}+1\) - n % 3 == 1
n 可以拆成 \(\frac{n-1}{3}-1\) , \(\frac{n-1}{3}\) , \(\frac{n-1}{3}+2\) - n % 3 == 2
n 可以拆成 \(\frac{n+1}{3}-2\) , \(\frac{n+1}{3}\) , \(\frac{n+1}{3}+1\)
- n % 3 == 0
直接判断3个数是否互质即可
样例甚至贴心的给出了唯一不可能的情况,他真的,我哭死
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;
int n;
void solve()
{
cin >> n;
if (n % 2) cout << 1 << endl;
else if (n == 6) cout << -1 << endl;
else if ((n / 2) % 2 == 0) cout << 2 << endl;
else
{
bool ok = false;
if (n % 3 == 1)
{
if ((n / 3) % 2 && (n / 3 - 1) % 3) ok = true;
}
else if (n % 3 == 2)
{
if (((n + 1) / 3) % 2 && (n / 3 - 1) % 3) ok = true;
}
else
{
if ((n / 3) % 2 == 0)
{
cout << 2 << endl;
return;
}
}
cout << (ok ? 3 : 4) << endl;
}
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
J. Joy of Handcraft
知识点:线段树 / 并查集
复杂度:\(O(mlog^2m)/O(mlogm)\)
这题一开始就验了线段树复杂度是对的,
但是队友线段树懒惰标记忘记清空导致一直没过样例,
线段树的bug还特别难找,熟练度还是低了
调了整整1个小时,虽然1发过
显然当 \(t\) 相同时 只保留最大的 \(x\) 即可
那么对于所有的 \(t=1,2,3,...,n\) 只会有1个答案
如果用线段树更新区间,那么所有的线段个数为 \(\frac{n}{2}+\frac{n}{3}+\frac{n}{4}+...+\frac{n}{n}\)
总和为 \(nlogn\), 乘上线段树区间修改的复杂度为 \(logn\),
总复杂度为 \(O(nlog^2n)\)
看了题解后发现还有并查集写法,具体操作就是并查集维护当前位置向后第一个没被染色的点
然后对染色区间的 \(x_i\) 从大到小排序,染完一个区间就将当前区间删除,染色次数就不会超过 \(O(m)\)
说来惭愧,写过原题却一点没印象
顺带一提,如果 \(ti>m\) 记得让 \(ti=min(ti,m)\)
否则很可能 RE 或者 WA
队友在debug到神志不清的时候把范围全改成1e5,导致一发过
这也在你的预料之中吗.jpg
线段树写法
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;
const int N = 1e5 + 5;
int n, m;
struct Segment_Tree
{
struct P
{
int l, r;
// 懒惰标记
ll lazy;
} p[N << 2];
void init_lazy(int id)
{
/* 初始化懒惰标记 */
p[id].lazy = 0;
}
void union_lazy(int fa, int ne)
{
/* 合并父子标记 */
p[ne].lazy = p[fa].lazy;
}
void cal_lazy(int fa, int ne)
{
/* 用父亲标记修改当子区间 */
}
void push_down(int id)
{
if (p[id].lazy/* 判断是否有懒惰标记 */)
{
if (p[id].l != p[id].r)
{
int ne = id << 1;
cal_lazy(id, ne);
cal_lazy(id, ne + 1);
union_lazy(id, ne);
union_lazy(id, ne + 1);
}
init_lazy(id);
}
}
void update(int id)
{
int ne = id << 1;
/* 合并左右子树 */
}
void build(int id, int l, int r)
{
p[id].l = l;
p[id].r = r;
init_lazy(id);
if (l == r)
{
/* 初始化单点区间信息 */
return;
}
int mid = (l + r) >> 1;
int ne = id << 1;
build(ne, l, mid);
build(ne + 1, mid + 1, r);
update(id);
}
void change(int id, int l, int r, ll d)
{
push_down(id);
if (l <= p[id].l && p[id].r <= r)
{
/* 修改懒惰标记 */
p[id].lazy = d;
cal_lazy(id, id);
return;
}
int mid = (p[id].l + p[id].r) >> 1;
int ne = id << 1;
if (r <= mid) change(ne, l, r, d);
else if (l > mid) change(ne + 1, l, r, d);
else
{
change(ne, l, r, d);
change(ne + 1, l, r, d);
}
update(id);
}
P sum(int id, int l, int r)
{
if (p[id].lazy) return p[id];
if (l <= p[id].l && p[id].r <= r) return p[id];
int mid = (p[id].l + p[id].r) >> 1;
int ne = id << 1;
if (r <= mid) return sum(ne, l, r);
return sum(ne + 1, l, r);
}
}T;
void solve()
{
cin >> n >> m;
T.build(1, 1, m);
vc<int> t(m + 1);
rep(i, 1, n)
{
int ti, xi; cin >> ti >> xi;
ti = min(ti, m);
t[ti] = max(t[ti], xi);
}
vc<pii> p;
rep(i, 1, m) if (t[i]) p.emplace_back(t[i], i);
sort(p.begin(), p.end());
for (auto u : p)
for (int i = 1; i <= m; i += u.se * 2)
T.change(1, i, min(m, i + u.se - 1), u.fi);
rep(i, 1, m) cout << T.sum(1, i, i).lazy << " \n"[i == m];
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
并查集写法
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;
const int mod = 1e9 + 7;
const int N = 1e5 + 5;
int n, m, k;
int f[N];
void bcj_init(int n) { iota(f, f + n + 1, 0); }
int find(int u)
{
if (f[u] == u)return u;
return f[u] = find(f[u]);
}
void solve()
{
cin >> n >> m;
bcj_init(m + 1);
vc<int> t(m + 1);
rep(i, 1, n)
{
int ti, xi; cin >> ti >> xi;
ti = min(ti, m);
t[ti] = max(t[ti], xi);
}
vc<pii> p;
rep(i, 1, m) if (t[i]) p.emplace_back(t[i], i);
sort(p.begin(), p.end(), greater<pii>());
vc<int> ans(m + 1);
for (auto u : p)
{
for (int i = 1; i <= m; i += u.se * 2)
{
int x = find(i), r = min(m, i + u.se - 1);
while (x <= r)
{
ans[x] = u.fi;
f[x] = x + 1;
x = find(x);
}
}
}
rep(i, 1, m) cout << ans[i] << " \n"[i == m];
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
L. Lottery
知识点:多重背包,找规律
复杂度:\(O(nlog^2n+nlogn)\) 优化后 \(O(nlogn)\)
这题其实很快就有思路了,但是队友卡在上一题的线段树太久了,导致一直没占到电脑
然后在拿到电脑时,一开始的写法让map的指针乱指导致怒WA一发
后来增加一点常数去掉了乱七八糟的指针就一发AC
- 观察样例1我们可以得到,如果每种 \(2^i\) 只有1个,那么答案明显是 \(2^n\)
- 如果数据范围比较小明显就是一个多重背包,但是该题的范围是1e9
- 那么按照多重背包的优化,我们将每一对 \(a_i\) 与 \(x_i\) 进行拆分
例如 \(a_i=2\) 与 \(x_i = 3\) 我们就拆成 \(2^2\) 与 \(2^3\)
换句话说就是,当 \(x_i>=(1<<k)-1\) 时就拆出 \((111...11)_{01}\) - 当全部拆完时,对于每一位 \(2^{a_i}\) 在该位保留1 的情况下向 \(2^{a_i+1}\) 进位
- 处理完进位后,对于每一位 \(2^{a_i}\),\(x_i\) 要么为 1,要么为2
- 对于不连续的 \(a_i\) 明显是乘法原则计数
- 对于连续的 \(a_i\) 如果该位为 1,则方案数为后缀方案数 × 2 × 前缀方案数
- 对于连续的 \(a_i\) 如果该位为 2,则方案数为后缀方案数 × (2 × 前缀方案数 + 1)
- 举例来说就是 \(12121\) 的方案数为 \(2×(2×2×(2×2+1)+1)\)
明显我们从后向前枚举 \(2^{a_i}\) 更方便计算
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
#define ll long long
#define fi first
#define se second
template<class T> using vc = vector<T>;
const int mod = 1e9 + 7;
const int N = 1e5 + 5;
int n, m, k;
map<int, int> mp;
void calc()
{
int a, x;
cin >> a >> x;
while (x)
{
auto &it = mp[a++];
x += it;
it = (x - 1) % 2 + 1;
x = (x - 1) / 2;
}
}
void solve()
{
mp.clear();
cin >> n;
rep(i, 1, n) calc();
ll ans = 1, tmp = 1;
for (auto it = mp.rbegin(); it != mp.rend(); it++)
{
if (it->se == 1) tmp = tmp * 2 % mod;
else tmp = (tmp * 2 + 1) % mod;
auto ne = next(it);
if (ne == mp.rend())
{
ans = ans * tmp % mod;
break;
}
if (ne->fi + 1 != it->fi)
{
ans = ans * tmp % mod;
tmp = 1;
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
优化后
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;
const int mod = 1e9 + 7;
const int N = 1e5 + 5;
int n, m, k;
pii a[N];
void solve()
{
cin >> n;
rep(i, 1, n) cin >> a[i].fi >> a[i].se;
sort(a + 1, a + n + 1);
vc<pii> p;
ll tmp(0);
rep(i, 1, n)
{
ll now = a[i].fi;
tmp += a[i].se;
if (i == n)
{
while (tmp)
{
p.emplace_back(now++, (tmp - 1) % 2 + 1);
tmp = (tmp - 1) / 2;
}
}
else
{
while (tmp && now != a[i + 1].fi)
{
p.emplace_back(now++, (tmp - 1) % 2 + 1);
tmp = (tmp - 1) / 2;
}
}
}
ll ans = 1, len = p.size() - 1; tmp = 1;
per(i, len, 0)
{
if (p[i].se == 1) tmp = tmp * 2 % mod;
else tmp = (tmp * 2 + 1) % mod;
if (!i || p[i].fi != p[i - 1].fi + 1)
{
ans = ans * tmp % mod;
tmp = 1;
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
G. Game of Cards
vp时没写出来的题,结论猜错了,果然博弈题还是要打表看sg函数
先打个表
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
array<int, 4> c;
const int sz = 7;
int dp[sz + 1][sz + 1][sz + sz / 2 + 1][2];
bool brute()
{
function<bool(array<int, 4>)> dfs = [&](array<int, 4> c) -> bool
{
auto &u = dp[c[0]][c[1]][c[2]][c[3]];
if (~u) return u;
bool ok = true;
if (c[0] >= 2) ok &= dfs({ c[0] - 1,c[1],c[2],c[3] });
if (c[0] && c[1] + c[2] + c[3]) ok &= dfs({ c[0] - 1,c[1],c[2],c[3] });
if (c[1] >= 2) ok &= dfs({ c[0],c[1] - 2,c[2] + 1,c[3] });
if (c[1] && c[2]) ok &= dfs({ c[0],c[1] - 1,c[2] - 1,c[3] | 1 });
return u = !ok;
};
return dfs(c);
}
void solve()
{
memset(dp, -1, sizeof(dp));
rep(i, 0, sz) rep(i1, 0, sz) rep(i2, 0, sz) rep(i3, 0, 1)
{
c = { i,i1,i2,i3 };
brute();
}
rep(i, 0, sz) rep(i1, 0, sz)
{
cout << string(i1, ' ');
rep(i2, 0, sz) cout << dp[i][i1][i2][0] << dp[i][i1][i2][1] << " \n"[i2 == sz];
}
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
solve();
}
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
00 00 00 00 00 00 00 00
00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
00 00 11 11 11 11 11 11
11 11 11 11 11 11 11 11
11 00 00 00 00 00 00 00
-
明显当 \(c_2>=2\) 时的规律十分好找
当 \(c_2>=2\) 时,\(c_0\%2==c_1\%3\) 时,先手必败 -
现在来看 \(c_2<2\) 时的情况
- \(c_0\),0,0,0 时,当 \(c_0\) 为奇数或者等于 0 时,先手必败
- \(c_2==0\) 时
- \(c_0\) 为偶数时,\(c_1\%3!=2\) 先手必败
- \(c_0\) 为奇数时,\(c_1\%3==2\) 先手必败
- \(c_2==1\) 时
- \(c_0\) 为偶数时,\(c_1\%3==0\) 先手必败
- \(c_0\) 为奇数时,\(c_1\%3!=0\) 先手必败
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;
const int N = 1e5 + 5;
int n;
array<int, 4> c;
void pr(bool fi_win)
{
cout << (fi_win ? "Rabbit" : "Horse") << endl;
}
void solve()
{
rep(i, 0, 3) cin >> c[i];
if (c[2] >= 2) pr(c[0] % 2 != c[1] % 3);
else if (!c[1] && !c[2] && !c[3]) pr(c[0] % 2 == 0 && c[0]);
else if (c[2])
{
if (c[0] % 2) pr(c[1] % 3 == 0);
else pr(c[1] % 3);
}
else
{
if (c[0] % 2) pr(c[1] % 3 != 2);
else pr(c[1] % 3 == 2);
}
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}
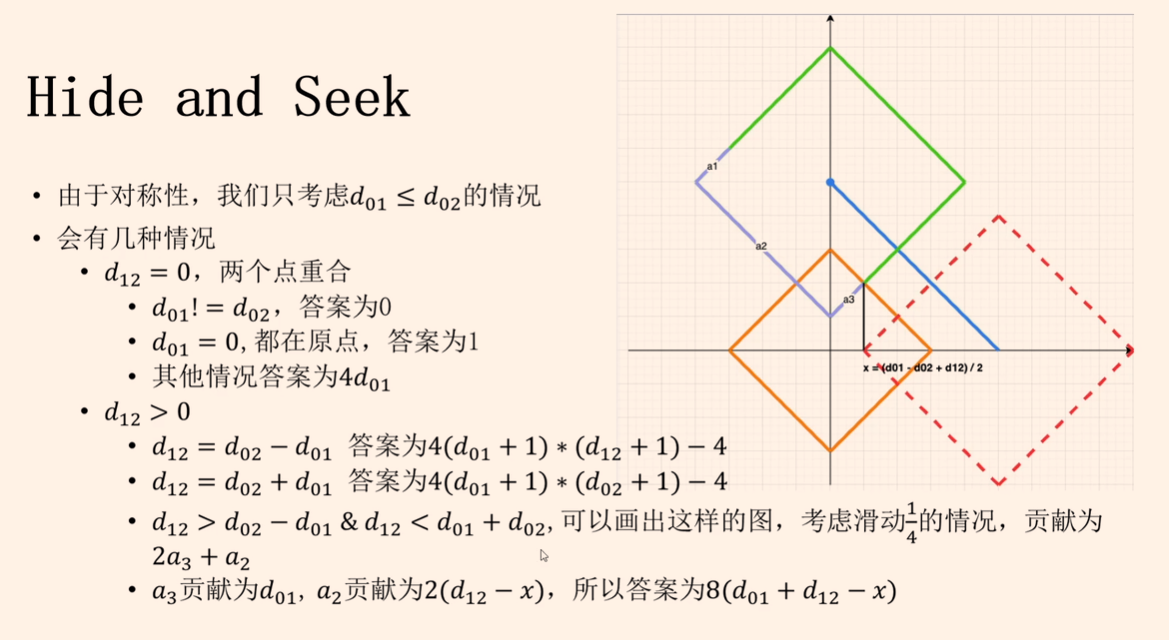
H. Hide and Seek
知识点:分类讨论
复杂度:\(O(1)\)
赛时甚至没看到这题,题解说的挺清楚的,确实不画图根本想不全
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
template<class T> using vc = vector<T>;
void solve()
{
ll d01, d02, d12, ans(0);
cin >> d01 >> d02 >> d12;
if (d01 > d02) swap(d01, d02);
if (d12 == 0)
{
if (d01 != d02) ans = 0;
else if (!d01) ans = 1;
else ans = 4 * d01;
}
else if (d12 == d02 - d01) ans = (d01 + 1) * 4 * (d12 + 1) - 4;
else if (d12 == d02 + d01) ans = (d01 + 1) * 4 * (d02 + 1) - 4;
else if (d12 > d02 - d01 && d12 < d01 + d02)
{
if ((d02 - d12 - d01) % 2) ans = 0;
else
{
ll x = (d01 - d02 + d12) / 2;
ans = 8 * (d01 + d12 - x);
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
int T = 1;
cin >> T;
rep(i, 1, T)
{
cout << "Case #" << i << ": ";
solve();
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号