广州2022CCPC补题
I Infection
知识点: 树上背包
第一次写树上背包的题目,没想到就是在区域赛中
神奇的是树上背包的复杂度,看起来是\(O(n^3)\),但是实际计算只有\(O(n^2)\)
学会树上背包后可以很明显[1]的发现这是一道树上背包的题目
而我认为该题思路的难点[2]在于想到先枚举被感染的点集,再确定起始感染点是哪一个
所以我们就可以定义dp状态:
1.该点集是否包含起始感染点
2.以u为根的子树
3.该点集内被感染的点数
如果已经学过树上背包,此时就十分好转移了
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;
const int mod = 1e9 + 7;
const int N = 2e3 + 5;
ll dp[2][N][N];
ll ksm(ll x, int n)
{
ll ret = 1;
while (n)
{
if (n & 1) ret = ret * x % mod;
x = x * x % mod;
n >>= 1;
}
return ret;
}
vc<int> h[N];
ll p[N], w[N], ans[N];
int sz[N];
void dfs(int u, int fa)
{
dp[0][u][0] = 1 - p[u]; //未选择初始感染点,u子树,0个感染点
dp[0][u][1] = p[u]; //未选择初始感染点,u子树,1个感染点
dp[1][u][1] = w[u]; //选择u为初始感染点,1个感染点
sz[u] = 1; //已合并节点个数
for (auto v : h[u])
{
if (v == fa) continue;
dfs(v, u);
vc<ll> dp0(sz[u] + sz[v] + 1, 0), dp1(sz[u] + sz[v] + 1, 0);
rep(i, 1, sz[u]) rep(j, 0, sz[v])
{
dp0[i + j] = (dp0[i + j] + dp[0][u][i] * dp[0][v][j]) % mod;
dp1[i + j] = (dp1[i + j] + dp[1][u][i] * dp[0][v][j] + dp[0][u][i] * dp[1][v][j]) % mod;
}
sz[u] += sz[v];
//更新dp状态
rep(i, 1, sz[u])
{
dp[0][u][i] = dp0[i];
dp[1][u][i] = dp1[i];
}
}
//统计答案
rep(i, 1, sz[u]) ans[i] = (ans[i] + dp[1][u][i] * (1 - p[fa])) % mod;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
//init
int n; cin >> n;
rep(i, 2, n)
{
int u, v; cin >> u >> v;
h[u].push_back(v);
h[v].push_back(u);
}
ll wi(0);
rep(i, 1, n)
{
int a, b, c;
cin >> a >> b >> c;
wi += w[i] = a;
p[i] = b * ksm(c, mod - 2) % mod;
}
wi = ksm(wi, mod - 2);
rep(i, 1, n) w[i] = w[i] * wi % mod;
//树上背包
dfs(1, 0);
//输出答案
rep(i, 1, n) cout << (ans[i] % mod + mod) % mod << endl;
return 0;
}
M XOR Sum
知识点: 数位dp
赛时属于是被1e15,1e13这么大的数据范围吓到了
赛后看到了枚举余数后立马想到了累计高位余数
不过我只能想到\(9×9=81\),以为对高位影响最多40
于是就写成了\(dp[45] [20] [45]\),被学长一眼看出不妥
高位余数至少需要\(80+40+20+10+5+2+1=158\)
所以要开\(dp[45] [20] [175]\),所以电子竞技菜是原罪
该题思维的难点在于如何处理如此巨大的 \(n\) ,
而看出通过计算高位余数后,如何处理异或和数位dp就变得十分显然
dp写法
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;
const int mod = 1e9 + 7;
const int FN = 25;
ll fac[FN];//阶乘数组
ll ifc[FN];//阶乘逆元
ll inv[FN];//逆元
void init(int n)
{
fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
rep(i, 2, n)
{
fac[i] = fac[i - 1] * i % mod;
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
ifc[i] = ifc[i - 1] * inv[i] % mod;
}
}
ll C(ll n, ll m)
{
if (n < m) return 0;
return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}
ll n, m, k;
ll dp[45][20][175];
int lim[45];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> k;
init(22); //预处理组合数
rep(i, 0, 40) lim[i] = (m >> i) & 1; //二进制拆分m
memset(dp, -1, sizeof(dp));
if ((n >> 41) > 170)
{
cout << 0 << endl;
return 0;
}
dp[41][k][n >> 41] = 1;
per(i, 41, 1) rep(j, 0, k) rep(t, 0, 170)
{
ll &u = dp[i][j][t]; //当前状态
if (u < 0) continue; //如果当前状态没被枚举过就跳过
int sum = t * 2 + ((n >> (i - 1)) & 1); //上一位遗留来的余数
if (lim[i - 1] == 0) //当前上界为0
{
rep(x, j, k)
{
if (x * (k - x) > sum) continue; //总和n被超过
if (sum - x * (k - x) > 170) continue; //总和n无法到达
ll &v = dp[i - 1][j][sum - x * (k - x)];//被更新状态
if (v < 0) v = 0;
v = (v + u * C(k - j, x - j)) % mod;
}
}
else //当前上界为1
{
rep(j2, 0, j) rep(x, 0, k - j)
{
if ((j2 + x) * (k - j2 - x) > sum) continue; //总和n被超过
if (sum - (j2 + x) * (k - j2 - x) > 170) continue; //总和n无法到达
ll &v = dp[i - 1][j2][sum - (j2 + x) * (k - j2 - x)]; //被更新状态
if (v < 0) v = 0;
v = (v + u * C(j, j2) * C(k - j, x)) % mod;
}
}
}
ll ans(0);
rep(i, 0, k) ans = (ans + (dp[0][i][0] > 0 ? dp[0][i][0] : 0)) % mod;
cout << ans << endl;
return 0;
}
dfs写法
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
template<class T> using vc = vector<T>;
template<class T> using vvc = vc<vc<T>>;
ll n, m, k;
const int mod = 1e9 + 7;
const int FN = 25;
ll fac[FN];//阶乘数组
ll ifc[FN];//阶乘逆元
ll inv[FN];//逆元
void init(int n)
{
fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
rep(i, 2, n)
{
fac[i] = fac[i - 1] * i % mod;
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
ifc[i] = ifc[i - 1] * inv[i] % mod;
}
}
ll C(ll n, ll m)
{
if (n < m) return 0;
return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}
ll dp[45][20][175];
int lim[45];
ll dfs(int w, int num, int sum)
{
if (sum < 0 || sum > 170) return 0;
if (w < 0) return sum ? 0 : 1;
if (~dp[w][num][sum]) return dp[w][num][sum];
ll &u = dp[w][num][sum]; u = 0;
int need = sum * 2 + ((n >> w) & 1);
if (lim[w])
{
rep(i, 0, num) rep(j, 0, k - num)
{
int x = (i + j) * (k - i - j);
u = (u + dfs(w - 1, i, need - x) * C(num, i) * C(k - num, j)) % mod;
}
}
else
{
rep(i, num, k)
{
int x = i * (k - i);
u = (u + dfs(w - 1, num, need - x) * C(k - num, i - num)) % mod;
}
}
return u;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> k;
init(22);
rep(i, 0, 40) lim[i] = (m >> i) & 1;
memset(dp, -1, sizeof(dp));
cout << dfs(40, k, n >> 41) << endl;
return 0;
}
J Math Exam
知识点: 折线模型,容斥
在看完题解后,学长扔过来一道题,说是原题....P3266 [JLOI2015]骗我呢
emmmmmm,怎么说呢,看完题解后,我满脑子都是: 这是人能想到的?
先看这题题面
[JLOI2015]骗我呢
题目描述
说起来,毕业之后 B 君也就见过 R 君两面而已。
R 君有一个 \(n \times m\) 的数组 \(x_{i,j}(1 \le i \le n; 1 \le j \le m)\)。
对于 \(1 \le i \le n; 1 \le j \le m\),满足\(0 \le x_{i,j} \le m\)。求 可能的数组\(x_{i,j}\) 的解数。
B 君觉得限制太宽松,还要求对于 \(1 \le i \le n; 1 \le j<m\),满足 \(x_{i,j} <x_{i,j+1}\),对于\(1 <i \le n; 1 \le j<m\),满足 \(x_{i,j} <x_{i-1,j+1}\)。
B 君认为 R 君可以直接 pwn 掉这个题。
R 君说:「黑的实在逼真 =.=,你起码把解数模 \(10^9+7\) 吧。」B 君觉得 R 君说的有道理,于是想让你求解数模 \(10^9+7\) 的结果。输入格式
一行两个整数表示 \(n, m\),含义如题目中所述。
输出格式
一行一个数表示同时满足 B 君和 R 君的条件 \(x_{i,j}\) 的解数,模 \(10^9+7\) 的结果。
样例 #1
样例输入 #1
3 3样例输出 #1
40提示
对于 \(100\%\) 的数据,\(1 \leq m, n \leq 10^6\)
我的水平只能支持我看懂dp和dp的简化
至于后面的模型转换,真的看了我几个小时
第一篇题解和第二篇题解在最后计算答案时开始变的无比抽象
比如我一开始完全没懂第一篇的字符串ABABA....是在干什么
第二篇计算答案这里的\(C_{2n+m+1}^{n}-C_{2n+m+1}^{n+m+2}-C_{2n+m+1}^{n-1}\)就完全不知道在说什么
其实就是没完全理解折线模型,或者说基本没做过相关题目,总结:就是菜
在看到这篇题解的时候才明白,原来是终点关于两条直线的对称点
明白这一点后,后面的容斥就十分自然,真的自然吗QAQ
这篇题解开头说的真的说到我心坎上了:
我人傻了啊……想了一两个小时,想出了个屁……这是什么东西哦……真的离天下之大谱!
理解完思路后,代码反而变得十分好写
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
const int mod = 1e9 + 7;
namespace cnm
{
const int FN = 3e6 + 5;
ll fac[FN];//阶乘数组
ll ifc[FN];//阶乘逆元
ll inv[FN];//逆元
void init(int n)
{
fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
rep(i, 2, n)
{
fac[i] = fac[i - 1] * i % mod;
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
ifc[i] = ifc[i - 1] * inv[i] % mod;
}
}
ll C(ll n, ll m)
{
if (n < m) return 0;
return fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;
int n, m;
ll A(ll x, ll y);
ll B(ll x, ll y);
ll A(ll x, ll y)
{
if (x < 0 || y < 0) return 0;
return (C(x + y, x) - B(y + 1, x - 1) + mod) % mod;
}
ll B(ll x, ll y)
{
if (x < 0 || y < 0) return 0;
return (C(x + y, x) - A(y - m - 2, x + m + 2) + mod) % mod;
}
int main()
{
cin >> n >> m;
cnm::init(n * 2 + m + 1);
ll ans = C(n * 2 + m + 1, n);
ans = (ans - A(n - 1, n + m + 2) + mod) % mod;
ans = (ans - B(n + m + 2, n - 1) + mod) % mod;
cout << ans << endl;
return 0;
}
在解决完学长扔出的题目后,开始尝试解决该题
显然我们能通过\(4S_i = a_i^2 + 2a_i+1\)化简得到
看完题解后,我们就有了第一步的模型转换
我的理解是:
- 绝对值为了处理\(a_i=-a_{i-1}\)
- 除2是为了让步长为1
- +1可能是为了变成折线模型
此时模型变成了 \(b_i\) 从 \((0,0)\) 出发,每次可以向右上或右下走
但是不能碰到直线 \(y = - 1\) 与 \(y = \frac{m+1}{2} + 1\)
为了变成折线模型,我们重新处理坐标系
将模型转换成 \(b_i\) 从 \((0,0)\) 出发,每次可以向上或者右走
但是不能碰到直线 \(y = x - 1\) 与 \(y = x + \frac{m+1}{2} + 1\)
此时模型就与上一题相似了
当 \(n=5\),\(m=3\) 时如图
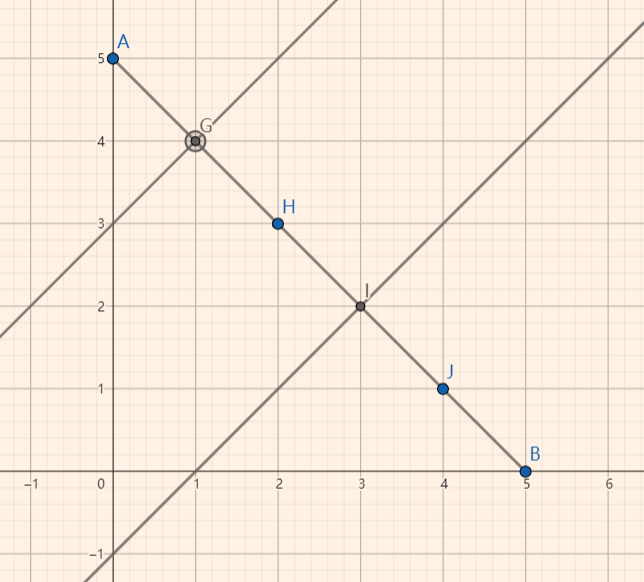
显然对于 A,G,H,I,J,B 就只有 H 有 \(C_5^2\) 种情况(包括不合法的情况)
然后对于碰到直线 \(y = x + 3\) 与 \(y = x - 1\) 的情况我们就需要进行容斥去除不合法的路线
于是我就写下了如下代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
template<class T> using vc = vector<T>;
const int mod = 998244353;
namespace cnm
{
const int FN = 1e7 + 5;
int fac[FN];//阶乘数组
int ifc[FN];//阶乘逆元
int inv[FN];//逆元
void init(int n)
{
fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
rep(i, 2, n)
{
fac[i] = (ll)fac[i - 1] * i % mod;
inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;
ifc[i] = (ll)ifc[i - 1] * inv[i] % mod;
}
}
ll C(ll n, ll m)
{
if (n < m || m < 0) return 0;
return (ll)fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;
ll ksm(ll x, ll n)
{
ll ret = 1;
while (n)
{
if (n & 1) ret = ret * x % mod;
x = x * x % mod;
n >>= 1;
}
return ret;
}
int n, m;
int main()
{
cin >> n >> m;
cnm::init(n);
vc<int> pre(n + 2, 0);
rep(i, 0, n) pre[i + 1] = ((ll)pre[i] + C(n, i)) % mod;
auto sum = [&](int l, int r) -> ll
{
l = max(l, 0);
r = min(r, n);
if (l > r) return 0;
return ((ll)pre[r + 1] - pre[l] + mod) % mod;
};
m = (m + 1) / 2;
ll l = (n - m + 1) / 2, r = n / 2;
ll ans = sum(l, r);
function<ll(int, int)> A, B;
A = [&](int l, int r) -> ll
{
l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
if (l > n || r < 0) return 0;
return (sum(l, r) - B(l, r) + mod) % mod;
};
B = [&](int l, int r) -> ll
{
l = n - l + 1, r = n - r + 1; swap(l, r);
if (l > n || r < 0) return 0;
return (sum(l, r) - A(l, r) + mod) % mod;
};
ans = (ans - A(l, r) + mod) % mod;
ans = (ans - B(l, r) + mod) % mod;
cout << ans << endl;
return 0;
}
但是问题来了,爆空间了,还是在我把4个 longlong 数组改成 int 的情况下爆空间了,所以我认为是栈空间爆了
那么就必须换写法了,我绝对不会说我看的杜老师代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rep(i,l,r) for(int i=l;i<=r;i++)
template<class T> using vc = vector<T>;
const int mod = 998244353;
namespace cnm
{
const int FN = 1e7 + 5;
int fac[FN];//阶乘数组
int ifc[FN];//阶乘逆元
int inv[FN];//逆元
void init(int n)
{
fac[0] = fac[1] = ifc[0] = ifc[1] = inv[1] = 1;
rep(i, 2, n)
{
fac[i] = (ll)fac[i - 1] * i % mod;
inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;
ifc[i] = (ll)ifc[i - 1] * inv[i] % mod;
}
}
ll C(ll n, ll m)
{
if (n < m || m < 0) return 0;
return (ll)fac[n] * ifc[m] % mod * ifc[n - m] % mod;
}
}
using cnm::C; using cnm::fac; using cnm::ifc; using cnm::inv;
ll ksm(ll x, ll n)
{
ll ret = 1;
while (n)
{
if (n & 1) ret = ret * x % mod;
x = x * x % mod;
n >>= 1;
}
return ret;
}
int n, m;
int main()
{
cin >> n >> m;
cnm::init(n);
vc<int> pre(n + 2, 0);
rep(i, 0, n) pre[i + 1] = ((ll)pre[i] + C(n, i)) % mod;
auto sum = [&](int l, int r) -> ll
{
l = max(l, 0);
r = min(r, n);
if (l > r) return 0;
return ((ll)pre[r + 1] - pre[l] + mod) % mod;
};
m = (m + 1) / 2;
ll l = (n - m + 1) / 2, r = n / 2;
ll ans = sum(l, r);
while (true)
{
l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
ans = (ans - sum(l, r) + mod) % mod;
l = n - l + 1, r = n - r + 1; swap(l, r);
ans = (ans + sum(l, r)) % mod;
if (l > n || r < 0) break;
}
l = (n - m + 1) / 2, r = n / 2;
while (true)
{
l = n - l + 1, r = n - r + 1; swap(l, r);
ans = (ans - sum(l, r) + mod) % mod;
l = n - l - m - 1, r = n - r - m - 1; swap(l, r);
ans = (ans + sum(l, r)) % mod;
if (l > n || r < 0) break;
}
cout << ans << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号