前 n 个自然数的和（一个无字证明）

我们要计算的是 \(S_n=1+2+\cdots+n\).

一个来源

知道计数原理的人应该就能看懂了。

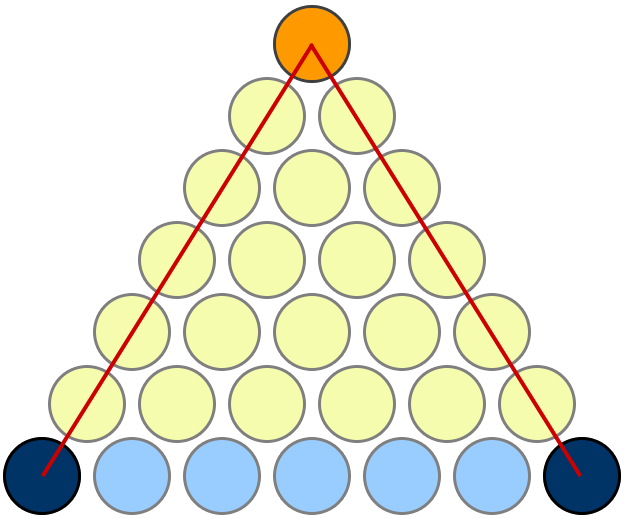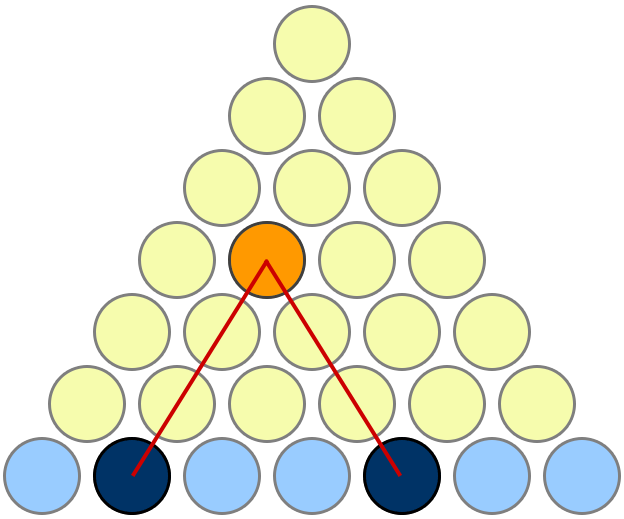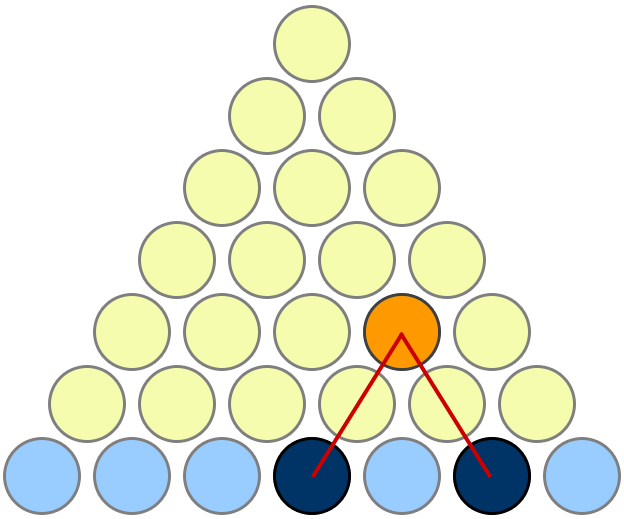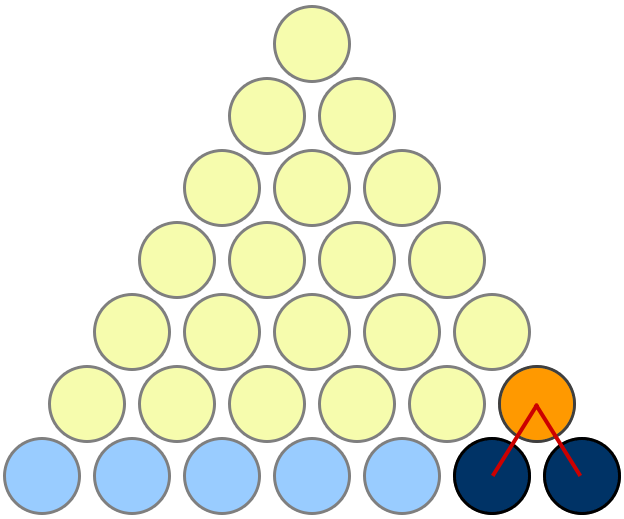
把前 \(n\) 个自然数如图表示，第 \(n\) 行放 \(n\) 个圆，一共有 \(n+1\) 行。故前 \(n\) 行共有 \(S_n\) 个圆。

按照图中的一一对应规则，\(S_n\) 个圆中的每一个都对应于最后一行中的一个“二选一”。于是我们只需算出对于 \(n+1\) 个圆共有多少种“二选一”选法即可。

假想它们如

_ _

放置，那么对于左边横线我们有 \(n+1\) 种选法，因为所有的球都可能被选到；对于右边的横线，我们有 \(n\) 种选择，因为有一个球刚才已经被选走了。所以共有 \(n(n+1)\) 种选择。这就是我们要的结果吗？不！你可以考虑这样一件事：你先选择最左边的球然后再选择最右边的球，与你先选择最右边的球再选择最左边的球得到的结果是一样的：都是那两个球。换到其他选择，情况都一样，选择的结果与顺序是无关的。也就是说，我们上面的计算结果还需要除以 \(2\)，才得到我们需要的“二选一”的种数 \(n(n+1)/2\)。

这样，我们就得到了 $$1+2+\cdots+n=\frac{n(n+1)}{2}.$$