Stacks of Flapjacks
原文链接 http://blog.csdn.net/yzfuture2010/article/details/8091337
有一堆煎饼，直径各异，摞成一堆。可用一把铲子插入任意两张饼之间，完成一次对铲子之上所有饼的翻转操作。假设最底部的饼的位置为1，最顶层的饼的位置为n。对第i (1≤i≤n) 张饼及其上的所有饼的一次翻转操作可以记为flip(i)。
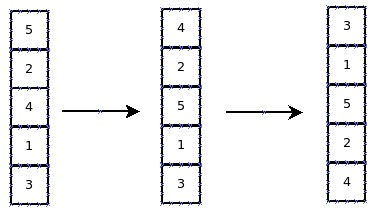
最左边一列经过flip(3)变为中间一列，而中间一列经过flip(1)变为最右边一列。
求算法，使得能对任意给出的一堆饼经过如上操作变为有序堆。堆中最小直径的饼在最顶层，最大直径的饼在最底层。
算法很简单，在n个饼组成的堆中找到直径最大的饼，假设其位置为m，作一次flip(m)操作。操作后，最大的饼就位于堆顶，然后再作一次flip(1)，使最大的饼处于最底层。由于底层的饼为最大，它肯定不会再参与后面的flip操作。接下来只需对剩余的n-1张饼作同样的操作即可，找到递归结构。
其中A为一个数组用以保存饼堆，n表当前饼堆的大小。
