强基计划校测备考游记
强基计划我爱你!!!!
高考游记可能会抽时间写的。但是现在考虑这个比。
2025.6.11
强基,好难
因式分解大师
大立方公式:
可以分解一些抽象东西。
已知 \(x^3 + 27y^3 + 9xy = 1\),求 \(x^3y\) 的取值范围。
key:我们有高水平因式分解,变形为 \(x^3 + (3y)^3 +(-1)^3- 3x(3y)(-1) = 0\),直接分解成 \((x+3y-1)(x^2+9y^2+1-3xy+x+3y)=0\)。
显然有 \(x+3y-1\) 是解,那么后面这个式子有没有解呢?
deepseek 说,直接大力求个判别式,得到 \(\Delta = -3(3y+1)^2 \le 0\),所以当且仅当 \(y=-\frac{1}{3}\) 的时候有解,此时解为 \((-1, -\frac{1}{3})\)。
所以其实所有的解是一条直线与一个单点。我自己做的时候成功没有考虑到还有个单点,悲伤了,数学好难。
取值范围很好求。
further thinking:二元有什么好的解决方案?
先换个元,一个比较简单的形式是 \(a^3 + b^3 + 3ab = 1\),这是一个对称的形式。
对称的多项式都可以表示成以 \((a+b), ab\) 为元的新多项式(多元就是 \(\sum x_i, \sum x_ix_j, \sum x_ix_jx_k \cdots\) 为元)
立即可得:\(u=1\) 或 \(3v = u^2 + u + 1\)。
考虑 \(x, y\) 是 \(t^2-ut+v = 0\) 的两根,则判别式 \(u^2-4v \ge 0\),带入 \(3v = u^2 + u + 1\) 有 \(\Delta = -\frac{1}{3}(u+2)^2 \ge 0\),立即有 \(u=-2, v=1\),解得 \(x=y=-1\)。
这个好像还有一定思维路径。
解 \((3x+y)^5 + x^5 + 4x + y= 0\)。
这个就简单了,显然可以令 \(a = 3x+y, b = x\),那就是 \(a^5 + b^5 + a + b = 0\)。
因式分解显然也可行,或者这个对称形式可以直接分离 \(a,b\),得到 \(a^5 + a = (-b)^5 + (-b)\),构造个函数 \(f(x) = x^5 + x\),显然单调,所以 \(a = -b, a + b = 0\),是一条直线。
对称式和轮换式咋处理啊??
好像一个基本思路是齐次化,但是我好像啥都不会。
\(a+b+c=a^2+b^2+c^2 = 0, a^3+b^3+c^3 = 3\),则 \(a^{2023} + b^{2023} + c^{2023}\) 的值为:
疑似是初中题(
但是我不会做啊
思路还是在用 \((a + b + c), (ab + ac + bc), abc\) 来整理式子。
有 \((a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc)\),由题直接得到 \(ab + ac + bc = 0\)。
考虑递推一下,令 \((a^n + b^n + c^n)(a+b+c) = (a^{n+1} + b^{n+1} + c^{n+1}) + (a^n(b+c) + b^n(a+c) + c^n(a + b))\)。
我做法是用 \(ab + ac + bc = 0\) 代换了一下,后面的式子变成 \(a^{n-1} (-bc) + b^{n-1} (-ac) + c^{n-1} (-ab) = -abc(a^{n-2}+b^{n-2}+c^{n-2})\),也就得到 \(a^n + b^n + c^n = abc(a^{n-3} + b^{n-3} + c^{n-3})\) 了。现在问题是求 \(abc\)。
还有一个 \(a^3+b^3+c^3 = 3\) 没用,用一下公式:\(a^3+b^3+c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-ac-bc) = 0\),直接得到 \(abc = 1\),那么发现这玩意就是个 \(3\) 为周期的东西了。
\(a, b, c\) 不全相等,\(a=ab+c, b=bc+a, c=ca+b\),求 \(a+b+c\) 的值。
这是个轮换的形式。我的想法大概就是把式子进行各种变形,然后通过式子的加法或者乘法得到一系列对称的关系式。好像这样是可以得到足够信息的?
我的没脑子做法:
首先全加起来,得到 \(ab + bc + ac = 0\)。
移项可以得到 \(a(1-b) = c, 1-b = \frac{c}{a}\)。同样的得到几个式子,加和可以得到 \((1-a)(1-b)(1-c) = 1\),拆开可以得到 \(-abc + (ab + ac + bc) - (a + b + c) = 0\),也就是 \(a+b+c = -abc\)。
直接把三个等式乘起来,得到 \(abc = a^2b^2c^2 + abc(a^2 + b^2 + c^2) + (a^2b^2 + a^2c^2 + b^2c^2) + abc\),也就是 \(a^2b^2c^2 + abc(a^2 + b^2 + c^2) + (a^2b^2 + a^2c^2 + b^2c^2) = 0\)。
显然有 \((a+b+c)^2 = (a^2 + b^2 + c^2) + 2(ab+bc+ac) = a^2 + b^2 + c^2\)。
由于 \(a-c = ab\),平方得到 \(a^2b^2 = a^2+c^2-2ac\),加起来有 \(a^2b^2 + a^2c^2 + b^2c^2 = 2(a^2+b^2+c^2) - 2(ab+ac+bc) = 2(a^2+b^2+c^2)\)。
至此所有的变量就都能换成 \(a+b+c\) 了,全部整理回去可以得到 \(3(a+b+c)^2 - (a+b+c)^3 = 0\)。如果 \(a+b+c = 0\) 的话,那么 \(abc= -(a+b+c) = 0\),\(a,b,c\) 中至少有一个为 \(0\),带回去式子检验发现成立不了。
这么做太麻烦了吧。有没有高人教我怎么做。
\(a+bc = b+ac = c+ba = 1\)。
相邻两项相等整理得到 \((a-b)(1-c) = 0\),又有 \(c+ba = 1, 1-c = ab\),那么就是 \((a-b)ab = 0\)。讨论一下 \(a=b, a=0, b=0\) 之类的就行了,解很有限。
我好菜,
可以先换元一下,可能好看一点。令 \(x \gets \frac{x}{3}\),得到 \(x^3 - y^2 - y = \frac{1}{3}\)。
这种问题可以分离两个变量,直接得到 \(x = \sqrt[3]{y^2 + y + \frac{1}{3}} = \sqrt[3]{(y + \frac{1}{2}) + \frac{1}{12}}\)。显然有 \(x > 0\),也就是里面函数是递增的。
设 \(f(x) = \sqrt[3]{(x + \frac{1}{2}) + \frac{1}{12}}\),那么就是 \(x = f(y), y = f(z), z = f(x)\),有 \(x = f(f(f(x)))\)。
哎这个函数单调递增欸,可以结合蛛网图来理解一下,这个 \(x\) 一定满足 \(x = f(x)\),也就是只有 \(x=y=z\) 的情况有解,然后只需要分析 \(x^3 - x^2 - x - \frac{1}{3} = 0\) 是否有有理数的解即可。
高人指点:有理根定理:如果整系数 \(a_nx^n + \cdots + a_1x + a_0 = 0\) 有有理数根,那么根 \(\frac{p}{q}\) 满足 \(p\) 为 \(a_0\) 的因子,\(q\) 为 \(a_n\) 的因子。
证明比较好说,直接带入得到 \(a_n p^n + a_{n-1} p^{n-1}q + \cdots + a_1 pq^{n-1} + a_0 q^n = 0\)。两边模 \(p\) 得到 \(a_0 q^n \equiv 0 \bmod p\),两边模 \(q\) 得到 \(a_n p^n \equiv 0 \bmod q\)。\(\gcd(p, q) = 1\),则 \(p | a_0, q | a_n\)。
零在上面。(?
那么根只有可能为 \(\pm 1, \pm \frac{1}{3}\)。带入发现不是,所以没有有理解。无理解直接分析函数,求导一下看就行,只有一个零点。
不等式呜呜呜
权方和不等式:\(\frac{a^2}{x} + \frac{b^2}{y} \ge \frac{(a+b)^2}{x+y}\)
我咋这个都不会。
简单题:证明
从 wikipedia 复制的。
简单题 2:Nesbitt 不等式
最后一步好像是排序不等式?
还是从 wikipedia 复制的。
死去的斐波那契数列攻击了我
有一个性质:\(a_{n+2} a_{n} - a_{n+1}^2\) 是以 \(-q\) 为公比的等比数列。这啥啊
可以大力整理,不过很麻烦
但是 wikipedia 给出的证明极其漂亮:
我们有熟知的矩阵表示二阶线性递推的方法:
我们可以考虑这个矩阵:
两边取行列式,立即得到:
这个太漂亮了。
用这个可以自然推广,任意的 \(f_{n+1} f_{n+p} - f_{n} f_{n+p+1}\) 也是一个公比为 \((-q)\) 的等比数列。nice.
这个性质逆性质也是成立的,由这个可以往后递推求每一项。
简单应用。
A 就是上面结论的直接应用,可以得到 \(a_{n+1}^2 - a_n a_{n+2} = -7\)。
B 带入几项就不对了。
C 与 D 容易发现这个 \(-7\) 可以换成上面那个式子,把 C 整理一下,把 \(a_{n+2}\) 换掉,就得到了等于 \((a_n - a_{n+1})^2\),正确。D 同样可以得到 \((a_n + a_{n+1})^2\),也正确。
2025.6.16
为什么隔了五天呢。因为我出去玩了。(真的)
ok 所以还是得学一下了。
我喜欢和自己复合
稳定点:如果 \(f(f(x)) = x\),那么称它为稳定点。也就是 \(f(x) = f^{-1}(x)\),即自己和自己反函数的交点。
不动点:\(f(x) = x\) 的点。
稳定点不一定在 \(y=x\) 上,单调减也不行,这需要注意。(死去的文化课好题攻击我:\(y=(1/16)^x\) 和 \(y=log_{1/16}(x)\) 过点 \((1/2, 1/4)\) 和 \((1/4, 1/2)\))
但是单调增就一定在了。同样的,单调增函数 \(f^n(x) = x\) 的解都是 \(f(x) = x\) 的解。
求方程 \(\left(\frac{x^3+x}{3}\right)+\frac{x^3+x}{3} = 3x\) 的所有实根的平方和。
令 \(f(x) = \frac{x^3+x}{3}\),实际上就是 \(f(f(x)) = x\)。这玩意单调递增,所以解就是 \(f(x) = x\) 的解。立马解出来了。
这东西类似于蛛网图那种感觉,画着理解一下。
微积分入门
有点弱智,秒完了。
分式线性递推
好结论啊,,
形如 \(a_{n+1} = \frac{a a_n + b}{c a_n + d}\)。
设 \(f(x) = \frac{ax+b}{cx+d}\)。如果 \(f(x)=x\) 有解,设不动点为 \(\lambda\),那么存在一个常数 \(t\),可以得到
proof 就是直接带入两个系数比一下。
那么由此可以两边取倒数,得到一个关于 \(\frac{1}{a_n - \lambda}\) 的线性递推,通项很好说了。
再细分一下,如果只有一个不动点那么可以得到 \(\frac{1}{a_n - \lambda}\) 是等差数列,如果有两个不动点,那么两个式子作比可以得到 \(\frac{a_n-\alpha}{a_n-\beta}\) 是一个等比数列。
如果没有不动点,那么很可能数列具有周期性。这条完全是经验公式,因为没有周期性的可能没啥好性质。大概可以想象成上面解出来的不动点是个复数,得到的大概是个公比为复数的玩意。一些情况下会是一个周期数列,其它情况可能就是一个没啥规律的带复数的玩意。
再来点结论:

妈的不想背结论,就这样吧,,
数列好难
浙江卷好像经常考这种抽象题,,
deepseek 的强大瞎jb分析能力给了一些启示:相当于 \(a_{n+1} - a_{n} = \frac{1}{a_n^2}\),如果用连续函数来近似一下的话就有一种 \(a'(n) = \frac{1}{a(n)^2}\),解个微分方程就得到了 \(a(n) = \sqrt[3]{3n+C}\),由 \(a_2 = 2\) 可以近似得到 \(a_n \approx a(n) = \sqrt[3]{3n+2}\)。
实际上这个近似还是不错的,我们甚至可以由此直接大胆猜测选 AB 走人。这种猜测还是比较有用的。
具体证明可以往上凑凑。两边三次方得到 \(a_{n+1}^3 = a_n^3 + 3 + \frac{3}{a_n^3} + \frac{1}{a_n^6}\)。
首先一步放缩容易得到 \(a_{n+1}^3 \ge a_n^3 + 3\),当 \(n \ge 2\) 的时候也就得到了 \(a_n \ge \sqrt[3]{3n+2}\)。
我们由 \(a_n^3 \ge 3n+2\) 往回带,可以得到另一个方向的不等式。有 \(a_{n+1}^3 \le a_n^3 + 3 + \frac{3}{3n+2} + \frac{1}{(3n+2)^2}\)。
这里好像是一些经典放缩:\(\ln \left(\frac{n + 1}{n}\right)\le \frac{1}{n} \le \ln \left(\frac{n}{n - 1}\right)\),\(\frac{1}{n(n+1)} \le \frac{1}{n^2} \le \frac{1}{n(n-1)}\),这样两者求和就都能做了。
把上面的式子放缩求和得到 \(a_n^3 \le 3n+2+\ln(n-1) + \frac{1}{9}\),这样可以得到一个 \(a_n\) 的范围了。
我们可以看到这个结果实际上和解微分方程得到的是差不多的,所以解微分方程确实是一个不错的估计方法。
那个浙江卷。可以解微分方程估计一个 \(a_n \approx \frac{3}{n + 2}\),直接选 B 走人了。证明和上面的很类似,也是先证明一个界然后带回去证明另一个界。
2025.6.17
高中没用上的数列放缩
ok i have no idea 这个应该怎么证明。
但是我会积分。
这个函数是递减的,所以可以立即得到 \(\sum_{i=1}^{2023} f(i) < \int_0^{2023}f(x) \mathrm{d} x < \int_0^{\infty}f(x) \mathrm{d} x = {\pi \over 2}\)
有没有人教我有没有普通证明方法。
反正我只做选择(
估计一下,\(\sqrt{\frac{2n-1}{4n^2+1}} \approx \sqrt{\frac{2n-1}{4n^2-1}} = \frac{1}{\sqrt{2n+1}} \approx \frac{2}{\sqrt{2n+1} + \sqrt{2n-1}} = \sqrt{2n+1} - \sqrt{2n-1}\)
然后求和 \(S_n \approx \sqrt{2n+1} - 1\)。估算大师。
这种二次递推好像很常见啊。包括上面那个浙江卷。
蛛网图很容易得到递增无界,\(x=2\) 是一个不动点,AB 正确。
然后 C 我确实没看出来。实际上套路完了,我可能真的菜把。
两边减 \(2\),可以得到 \(a_{n+1} - 2 = (a_n - 2)(a_n - 1)\),取倒数得到 \(\frac{1}{a_{n+1}-2} = \frac{1}{a_n - 2} - \frac{1}{a_n - 1}\),那么 \(\frac{1}{a_n - 1} = \frac{1}{a_n - 2} - \frac{1}{a_{n+1}-2}\)。这下求和很简单了,直接得到求和极限就是 \(\frac{1}{a_1 - 1} = 1\)。
高中数学题(kinda)
这题记忆很深刻啊,高三买的某本卷子上有这题。当时我做出来还觉得自己挺厉害的。
首先余弦定理和正弦定理可以整理成 \(\frac{ab\sin C}{3a^2 + 3b^2 + 4ab\cos C} = \frac{\sin C}{3(a/b)^2 + 3(b/a)^2 + 4\cos C} \le \frac{\sin C}{6 + 4\cos C}\),然后对他求导就行了。
两次放缩能取到极值的原因是两次分别对 \(C\) 和 \(\frac{a}{b}\) 求得极值,考虑固定 \(C\) 时,相当于一个外接圆上动点 C,\(\frac{a}{b}\) 是可以取遍 \(R^\star\) 的。
这个其实还挺有趣的。
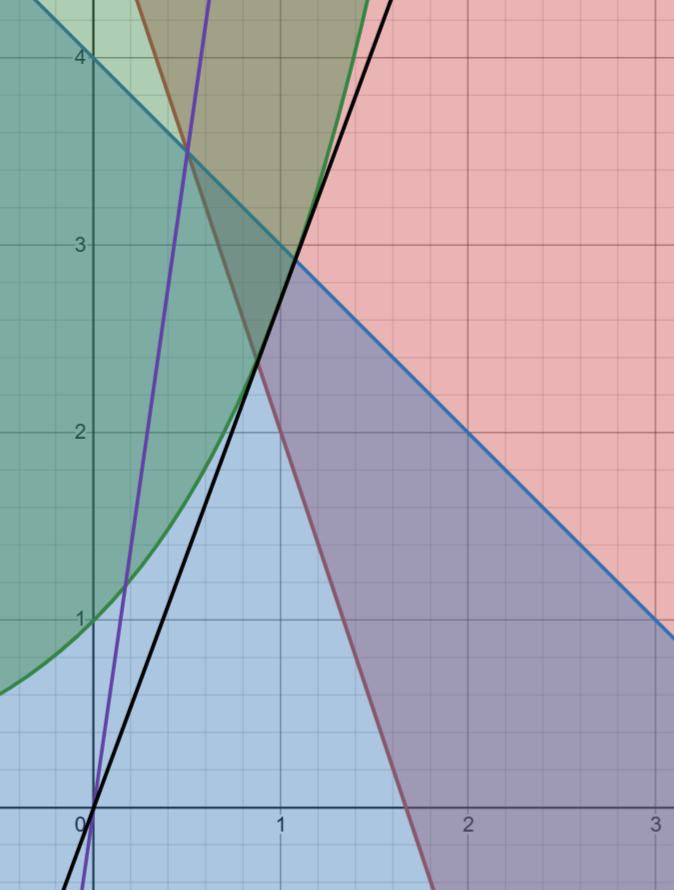
首先第二个式子整理一下可以得到 \(\ln(\frac{b}{c}) \ge \frac{a}{c}\),那么同理第一个式子发现也可以整理成 \(5-3 \frac{a}{c} \le \frac{b}{c} \le 4-\frac{a}{c}\)。令 \(y=\frac{b}{c}, x = \frac{a}{c}\),那么我们就是要求 \(\frac{y}{x}\) 的取值。
我们有:
\[\begin{cases} 5-3x \le y \le 4-x\\ y \ge e^x \end{cases} \]哇喔这不是线性规划吗(旧教材上的高中知识也是高中知识!)
不完全是,因为有一个不是线性的)不过完全可以用相同的思路来做,直接在直角坐标系上找到这个封闭图形,那么 \(\frac{y}{x}\) 就是斜率的范围,一个在上面切一个在下面切。上面就是两条直线的交点,下面正好是 \(y=ex\) 与 \(y=e^x\) 相切,切点在 \(x=1\) 上,可以切到。所以取值就是 \([e, 7]\)。
不等式还是一生之敌
已知 \(ab(a+8b)=20\), \(a, b > 0\), 求 \(a+3b\) 最小值。
我不会做,有没有人教我。
deepseek 上来求根公式,差完了,波特做法。
还给了个比值代换。令 \(b = ka\),那么 \(k(1+8k)a^3 = 20\),求 \((1+3k)a = (1+3k)\sqrt[3]{\frac{20}{k(1+8k)}}\) 最小值。这也不好做啊。
还给了个拉格朗日乘数法。也算是能做吧,确实做出来了,,
用线性规划那种想法,我直接找导数为 \(-\frac{1}{3}\) 的点,然后得到的也是这个结果,也行吧。
正经做法:目的是想办法凑出 \(x+3y\)。我们可以瞎整一个系数 \(ab(a+8b) = \frac{1}{2} 2a \cdot b \cdot (a + 8b) \le (\frac{2a + b + a + 8b}{3})^3 = (a + 3b)^3\)。
哇喔!这不是做出来了?没事,取等取不到。
所以我还是不会做嘛。其实需要特殊凑一下这个系数,使得取等能够取到。设两个系数为 \(x, y\),那么就是 \(xa \cdot yb \cdot (a + 8b) \le (\frac{(x + 1)a + (y+8)b}{3})^3\),我们需要 \(\frac{x+1}{y+8} = \frac{1}{3}\),即 \(3x-y = 5\)。
取等条件是 \(xa=yb=a+8b\)。联立一下,有 \(x = \frac{8b}{a} + 1, y = \frac{a}{b} + 8\),带入 \(3x-y = 5\) 得到 \(24b^2 - 10ab - a^2 = (12b+a)(2b-a) = 0\),有 \(a=2b\),那么 \(x=5, y=10\)。
那么有! \(1000 = 5a \cdot 10b \cdot (a+8b) \le (2a+6b)^3\),所以 \(a+3b \ge 5\)。
其实这么做得到的方程和直接求导令 \(b' = -\frac{1}{3}\) 得到的方程是一样的?同样能得到 \(a=2b\)。神奇。
ok this is not too hard
显然最大值应该是正负正负正,设 \(a>e\),那么写一下就发现结果是 \(2(|a| + |b| + |c| + |d|)\)。直接令 \(e=0\),那么就是 \(a^2 + b^2 + c^2 + d^2 = 1\),那么 \(2(|a| + |b| + |c| + |d|) \le 8\sqrt{\frac{a^2 + b^2 + c^2 + d^2}{4}} = 4\)。
似乎是个标准形式的不等式题。哈哈我不会不等式啊??
basic idea:往分母相同的方向去凑。
有 \(\sqrt{\frac{a}{b+c}} = \frac{a}{\sqrt{a(b+c)}} \ge \frac{2a}{a+b+c}\),那么显然原来的式子就能 \(\ge 2\) 了。取等条件为 \(a=b+c, b=a+c, c=a+b\) 的时候取等。其实能得到 \(a=b=c=0\),实际上上面的过程中上下乘了 \(a\),所以这个等号不能直接取。不过可以发现 \(a=0, b=c=1\) 就恰好等于 \(2\) 了,所以这个等号还是能取到的。所以最小值就是 \(2\)。最大值显然正无穷。
2025.6.18
调整法好神奇
琴生不等式:对于一个下凸函数(\(f''(x) \ge 0\)),有 \(\frac{\sum f(x_i)}{n} \ge f(\frac{\sum x_i}{n})\)。
上凸类似。可以想象一下割线大于或小于中点位置的函数值。
调整法:以下凸函数为例子,我们考虑将其中两个数往中间移动(或往两边移动)会发生什么。设两个数 \(x \le y\),移动 \(\Delta\),那么可以证明:
那么就说明,将两个数往两边移动会使和变大,那么最小值应当在全相等时取到,否则存在更小值。
proof:consider \(f(x) - f(x - \Delta)\) 与 \(f(y+\Delta) - f(y)\) 的大小,即 \(\int_{x-Delta}^{x} f'(t)\mathrm{d}t\) 与 \(\int_{y}^{y+\Delta} f'(t)\mathrm{d}t\) 的大小,两者区间长度相同,且对应位置前者小于后者,积分后整体小于。写一下就是 \(\int_{y}^{y+\Delta} f'(t)\mathrm{d}t = \int_{x-\Delta}^{x} f'(t - y + x - \Delta)\mathrm{d}t\),有 \(t \le t - y + x - \Delta\),即 \(f'(t) \le t-y+x-\Delta\),则 \(\int_{x-\Delta}^{x} f'(t)\mathrm{d}t \le \int_{x-\Delta}^{x} f'(t - y + x - \Delta)\mathrm{d}t\),即 \(f(x) - f(x - \Delta) \le f(y+\Delta) - f(y)\)。
这就是一个直接应用。\(\sqrt{4x+1}\) 显然是上凸的,那么琴生不等式直接得到最大值,最小值根据调整法,\(a=b=-\frac{1}{4}\) 时取得最小值。
如果有两个数 \(x <= y\),把他变成 \(x-1, y+1\),则有 \((x-1)^2 + (y+1)^2 = x^2 + y^2 + 2(y-x) + 2 > x^2 + y^2\)。所以最小值在所有相等(相差 \(1\))的时候取到,即 40 个 2 和 10 个 3 时取得。
最大值就是另一个方向,如果有两个数 \(>1\) 则可以操作一次使得和更大,所以最大值在 49 个 1 和 1 个 61 的时候取到。
好难,我居然还做出来了,不知道咋做的。
首先因式分解大师,得到这个式子就等于 \((a-b)(b-c)(a-c)\)。我们令 \(a \ge b \ge c\)。(\(a \le b \le c\) 的时候式子 \(<0\),且实际上就是原式子乘 \(-1\)),
下面令 \(p = a-b, q = b-c\),限制为 \(p, q, c > 0\),且 \(a + b + c = p + 2q + 3c = 1\),那么有 \(p + 2q \le 1\)。
在此条件下最大化 \(pq(p+q)\)。
此时可以无脑令 \(p + 2q = 1\),然后带入求导。或者你傻逼的话可以用前面用到的方法去凑基本不等式的系数,我就是这个傻逼。不过确实能做出来。
三角函数我谢谢你
因为我太菜了,不等式实在做不下去了,于是跳了。
妈的,这个更抽象。喜欢考结论。
证明就是把 \(\cos(\alpha + i\beta) \sin(\frac{\beta}{2})\) 积化和差,然后就能裂项了。
证明是 \(\cos(x) = \frac{\sin(2x)}{2\sin(x)}\),然后还是裂项。
joke3579 告诉我:\(\arctan(\frac{2}{k^2}) = \arctan(n+1) - \arctan(n-1)\)。
好抽象,这我哪年能想到。
2025.6.19
三角哈哈哈哈哈哈哈哈
\((1+\cos\frac{\pi}{7})(1+\cos\frac{3\pi}{7})(1+\cos\frac{5\pi}{7})\)
这个其实是能做的,我还是应该多试试。
直接拆开,得到一堆玩意。首先 \(\cos\frac{\pi}{7} \cos\frac{3\pi}{7}\) 这种项直接积化和差拆开,然后发现正好可以和一次项消掉。也就是结果为 \(1 + \cos\frac{\pi}{7}\cos\frac{3\pi}{7}\cos\frac{5\pi}{7}\)。
换一下其实等于 \(1 + \cos\frac{\pi}{7}\cos\frac{2\pi}{7}\cos\frac{4\pi}{7}\),用前面那个公式就行了,等于 \(-\frac{1}{8}\)。
一些 extra:对于 \(n\) 倍角,存在整系数多项式 \(\cos nx = f(\cos x)\)。令 \(\cos(7x) = -1\),解就是 \(\frac{\pi}{7}, \frac{3\pi}{7}, \frac{5\pi}{7}\) 之类的。那么实际上 \(\cos \frac{\pi}{7}, \cos \frac{3\pi}{7}, \cos \frac{5\pi}{7}\) 应当是某个多项式的根。实际上有 \(8x^3 - 4x^2 - 4x + 1= 0\),这也就解释了为什么很多这种相同形式的加或乘是有理数了。

所以理论来讲,所有 \(\cos(\frac{(2k+1)\pi}{n})\) 的对称式子都是有理的。并且对于奇数的 \(n\),\(\sin(\frac{k\pi}{n})\) 也有理。
但是实际用起来可能比较菜,因为大概也没人会去因式分解一个七次多项式。可能只有 deepseek 会这么干了。
有个结论:\(\prod_{i=1}^{n-1} \sin (\frac{i\pi}{n}) = \frac{n}{2^{n-1}}\)。证明先咕了,回头补。
憋笑,题怎么少个条件。搜了才知道,还以为若智题。
应该是 三角形 ABC。
应该得相信自己,大力化简就好了。
\[\begin{aligned} \cos^2A + \cos^2B + \cos^2 C = 1\\ \cos^2A + \cos^2B + \cos^2(A+B) = 1\\ \cos^2A + \cos^2B + (\cos A\cos B - \sin A \sin B)^2 = 1\\ \cos^2A + \cos^2B + \cos^2A\cos^2B + \sin^2A \sin^2B -2\sin A\cos A\sin B\cos B= 1\\ \cos^2A + \cos^2B + \cos^2A\cos^2B + (1-\cos^2A)(1-\cos^2B) -\frac{1}{2} \sin 2A \sin 2B= 1\\ 2\cos^2A\cos^2B - \frac{1}{2} \sin 2A \sin 2B= 0\\ \frac{1}{2}(1+\cos 2A)(1 + \cos 2B) - \frac{1}{2} \sin 2A \sin 2B= 0\\ \cos 2A\cos 2B - \sin 2A \sin 2B + \cos 2A + \cos 2B + 1= 0\\ \cos (2(A+B)) + 2\cos(A+B) \cos(A-B) + 1= 0\\ 2 \cos^2(A+B) + 2\cos(A+B) \cos(A-B)= 0\\ 2 \cos^2(A+B) + 2\cos(A+B) \cos(A-B)= 0\\ \cos A \cos B \cos C= 0\\ \end{aligned} \]我知道 latex 很丑。
哈哈。所以有一个是 \(\frac{pi}{2}\),然后极值显然是 \(\sqrt{5}\)。
几何更是一点不会
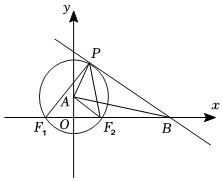
key:\(|F_1F_2|\) 固定,我们要最大化 \(\angle F_1PF_2\),即 \(\sin \angle F_1PF_2 = \frac{|F_1F_2|}{2R}\),我们只需要最小化 \(R\),也就是使得 \(\triangle F_1PF_2\) 的外接圆恰好与直线相切时 \(R\) 最小。
当然可以直接大力解方程,就是这个圆心好像不是很好解的样子。
几何一点:两个部分
弦切角定理:弦切角等于圆心角的一半,即等于圆周角。(我去这是不是物理里面讲的)
那么就有 \(\angle F_2PB = \angle BF_1P\),也就有 \(\triangle BF_2P \sim \triangle BPF_1\)。(please remember this)
则我们要求的 \(\frac{PF_1}{PF_2} = \frac{PB}{F_2B}\)。
圆幂定理
直接得到 \(PB^2 = BF_2 \cdot BF_1\),然后就都解出来了。
托勒密定理:对于一个圆的内接四边形,有 \(AC \times BD = AB \times CD + AD \times BC\)。
托勒密不等式:对于一个任意四边形,有 \(AC \times BD \le AB \times CD + AD \times BC\)。
设两个对角线夹角为 \(\alpha\),那么有 \(S = \frac{1}{2} AC \times BD \times \cos \alpha\)。有 \(S \le \frac{AB \times CD + BC \times AD}{2}\),当且仅当 \(\alpha = \frac{\pi}{2}\) 且为内接四边形时取等。那么就很明晰了。
补习因式分解
被因式分解整自闭了。补习一下。
主元法:把一个玩意当主元,其它的当常数来分解。尽量选次数比较小的字母当主元(不超过二次?),然后可以使用十字交叉等方法分解。
选取 \(2\) 为主元,那么就有:
然后十字交叉分解就很容易得到 \(b(a+b) + a(a-b) = a^2 + b^2\) 了。
均值换元:换成均值得到一个比较对称的形式。
令 \(t = x+2\),这样拆的时候可以消掉很多式子。
令 \(t = x+4\),则
\((t^2-1)(t^2-9) = t^4 - 10t^2 + 24 = (t^2-4)(t^2-6)\)
和积换元:就是对称式子可以用 \(a+b, ab\) 换元,前面用过好多次了。
试根法:本质因式定理。我们选取一个为主元 \(a\),对于最高次项与最低次项(常数)的系数,一定是各个因式的 \(a\) 系数与常数的乘积。于是我们可以通过对这两个系数分解,然后尝试根来得到其中一个因式。这个对于字母同样有用。
example:
我们以 \(x\) 为主元,得到 \(x^2\) 系数为 \(y\),常数为 \(y^2z-yz^2=yz(y-z)\),我们可以尝试 \(x=\pm y, x=\pm z, x=\pm (y-z), x=\pm \frac{y}{y}, x=\pm \frac{z}{y}, x=\pm \frac{y-z}{y}\) 等根。发现 \(x=y\) 为一个根。而由于这个式子是轮换的,可以立刻得到一定有因式 \((x-y)(y-z)(z-x)\)。而这已经是三次的了,所以只差一个前面的系数了,比对某一项即可。
和刚才思路一样,可以直接试 \(x=y\) 发现是可以的,于是有因式 \((x-y)(y-z)(z-x)\)。此时差一次,而这个一次的式子一定也是轮换的,一次的轮换式只有 \(x+y+z\),所以最后一个因式一定是 \(x+y+z\)。然后还是差一个系数。
常数为 \(b^3+c^3=(b+c)(b+c-bc)\),可以试得根 \(a=-(b+c)\),于是有一个因式为 \((a+b+c)\)。剩下两次,二次的轮换式有 \((a^2+b^2+c^2)\) 和 \(ab+bc+ca\)。可以通过待定系数来考虑,然后再比对系数。通过 \(a^3\) 的系数为 \(1\) 可以得到 \((a^2+b^2+c^2)\) 的系数为 \(1\),通过 \(abc\) 的系数为 \(-3\) 可以得到 \((ab+bc+ca)\) 的系数为 \(-1\)。
2025.6.20
复数哈哈
感觉其实不难。
可以设一个比值,令 \(\frac{x}{y} = -\frac{\bar{w}}{\bar{z}} = k\),立即有 \(|x^2| + |y^2| = (1+|k|^2)|y^2|\),右边同理,即可得到 \(|y| = |z|, |x| = |w|\)。
C 选项显然不对。D 选项疑似题打错了,我作业帮搜到的题是 \(|xw-yz|=1\),,
那么其实就不是很难了。我们可以用 \(x=r_x e^{\theta_x i}\) 来表示一下(其实就是三角表示,这样写方便很多),那么有 \(e^{(\theta_x - \theta_z)i} + e^{(\theta_y - \theta_w)i} = 0\),即 \(e^{(\theta_x + \theta_w)i} + e^{(\theta_y + \theta_z)i} = 0\),带入 \(xw-yz\) 就得到它等于 \((|x|^2 + |y|^2) e^{(\theta_x + \theta_w)i}\),模长显然等于 \(1\)。
对不起,我还是菜
key: 虚根的共轭成对出现。证明就是把整个方程取共轭仍然成立。
实系数方程,所以四个根应当为 \(x, \bar{x}, y, \bar{y}\)。
那么实际上条件就是 \(x+y=2+i, \bar{xy} = 5+6i, xy=5-6i\)
\(b = \sum x_ix_j\),分一下组就是 \(b = (x+y)(\bar{x} + \bar{y}) + xy + \bar{xy}\)。全有了。
非常自信的做错了,,
我是若智
显然换元,重点是 \(x^5 + \frac{1}{x^5} = t\) 的解的模长。实际上如果 \(z^5\) 都是复数了,那么考虑三角表示,虚部是 \(r\sin \theta - \frac{1}{r} \sin \theta\),显然这东西等于 \(0\) 的解是 \(r=1\),所以模长就是 \(1\)。
伏笔回收,,
首先有个结论:\(|1-\omega_n^k| =2\sin{\frac{k\pi}{n}}\)。可以用正弦定理证,直接带入也行。
然后有一个经典操作:考虑多项式 \(x^n-1 = (x - 1) \prod_{k=1}^{n-1} (x-\omega_n^k)\),并且 \(\sum_{k=0}^{n-1} x^k = \prod_{k=1}^{n-1} (x-\omega_n^k)\)。我们可以左右赋值来得到一些东西。
首先令 \(x=1\),两边取模长,就可以得到 \(n = \prod 2\sin{\frac{k\pi}{n}}\),所以可以得到 \(\sin{\frac{k\pi}{n}} = \frac{n}{2^{n-1}}\)。
然后第二个问题,我们可以首先把共轭的单位根配对,也就得到 \(\frac{x^7-1}{x-1} = (x^2 - (\omega_7 + \omega_7^6)x + 1)(x^2 - (\omega_7^2 + \omega_7^5)x + 1)(x^2 - (\omega_7^3 + \omega_7^4)x + 1) = (x^2 + 1 - 2\cos{\frac{2\pi}{7}}x)(x^2 + 1 - 2\cos{\frac{4\pi}{7}}x)(x^2 + 1 - 2\cos{\frac{6\pi}{7}}x)\)。这样我们得到了一个关于 \(\cos\) 的连乘式。
我们令 \(\frac{x^2+1}{-2x} = \frac{1}{2}\),解得 \(x = \omega_3\),于是我们赋值即可得到连乘式子。注意到这种做法可以求出任意 \(\prod (a+b \cos(\frac{2k\pi}{n}))\)。
计数原理与概率统计
太简单了,杀光了。
我爱数论
这个感觉还是比较有趣的。
不定方程:两种思路
一个是因式分解,另一个是不等式放缩。
因式分解:一般会通过常数的加减进行因式分解,使得左边为一个分解形式,右面是一个正整数,这样就可以通过枚举正整数的因子来解方程。
求 \(x^2-xy-2x+3y=11\) 的正整数解。
尝试将 \(x^2-xy-2x+3y\) 因式分解。注意我们可以任意加常数。首先从二次开始,由 \(x^2 - xy\) 得到两个因式 \(x, x - y\),然后再凑常数,由 \(-2x\) 和 \(3y\) 得到两个常数,因式分解为 \((x-3)(x-y-2)\),常数为 \(6\)。那么我们就可以得到 \((x+3)(x-y-2) = 17\),立即得到 \(x+3=17, x-y-2 = 1\),即 \(x=14, y=11\)。
求解不定方程 \(x^3-y^3=xy+61\)。
尝试凑大立方公式。有 \(27x^3 - 27y^3 - 1 - 27xy = 61 \times 27 - 1\),即 \((3x-3y-1)(9x^2+9y^2+1+9xy+9x-3y) = 61 \times 27 - 1 = 1646 = 2 \times 823\)。\(3x-3y-1 = 2\) 或 \(3x-3y-1=823\),后者无解(\(\bmod 3\) 考虑),所以 \(x-y=1\),代入原方程即可求解。
这种题好像很经典了。不过我不会做,哈哈。
考虑找一个界,假如 \(x > 6\) 那么 \(\frac{1}{x} + \frac 1 y + \frac 1z < \frac 12\),不行。所以有 \(3 \le x \le 6\)。
枚举一下,对于 \(3, 4, 6\),可以得到一个形如 \(\frac{1}{y} + \frac{1}{z} = \frac{1}{6}\) 之类的形式。拆成 \(yz = 6y+6z\)。这个形式是可以因式分解的,可以得到 \((y-6)(z-6)=36\),然后很好解了。
\(5\) 的时候得到一个 \(3yz=5(y+z)\),好像没法因式分解。可以用相同的办法找一个上界然后枚举。deepseek 说可以 \(y=\frac{5z}{3z-5}\),令 \(t = 3z-5\),然后就有 \(y=\frac{5t+25}{3t}\),一定有 \(t | 25\),然后枚举。
不等式放缩:
配方一下。可以凑成 \((3y-x)^2 + 2(x-3)^2 = 3\),这个显然 \((x-3)^2 = 1, (3y-x)^2 = 1\)。
显然条件是 \(x-1 | y+1\) 之类的。设 \(x\) 为最小值,那么有 \(x-1 < y+1 \Rightarrow x-1 \le \frac{y+1}{2}\),再由 \(y-1|z+1, z-1|x+1\) 得到 \(y-1 \le z+1, z-1 \le x+1\),那么联立一下就能得到 \(x \le 7\)。可以试 \(x=7, y=9, z=11\),正好可行,显然这就是最大值了。最小值就是 \(2, 2, 2\)。
\((x^2-y^2)^2 = 1 + 16y\)
显然 \(x \ne y\),那么就有 \(x \ge y+1\) 或者 \(x \le y-1\)。那么 \((x^2-y^2)^2 \ge (2y-1)^2\)。也就有 \(1+16y \ge (2y-1)^2\),可以解得 \(0 \le y \le 3\),带入检验即可。
一类特殊的不等式:对于判断是否能为完全平方数或完全立方数,可以考虑找到其与 \(x^2, (x+1)^2\) 的大小关系,如果 \(x^2 < y < (x+1)^2\),那么 \(y\) 一定不是完全平方数。同样可以用这种方法来确定一个范围然后枚举。
\(x^3 = y^3 + 2y^2 + 1\)
因为 \((y+1)^3 - (y^2 + 3y)= x^3\),并且 \(2y^2 + 1 > 0, x^3 > y^3\),如果 \((y^2 + 3y) > 0\),那么就有 \(y^3 < x^3 < (y+1)^3\),一定无解。所以 \(y^2 + 3y \le 0\),则 \(-3 \le y \le 0\),带入检验。
设 \(x > y\),那么有 \(x^2 < x^2 + 2y < x^2 + 2x < (x+1)^2\),显然 A 就不对了。
考虑 B,有 \(x^2 < x^2 + 4y < x^2 + 4x < (x+2)^2\),那么只可能为 \(x^2 + 4y = (x+1)^2\),即 \(4y-2x=1\),显然不可能。
C 与 D 可以用类似的方法分析。枚举平方,然后带入 \(y^2+6x\) 看看能否为完全平方数即可,一模一样的做法。
2025.6.21
时间不多了!!!
但是我还是在摆烂,,
组合好难
还比较有趣的题。我可能不会这么想,菜。
我们每次选出 \(27\) 个人,其中一定有一个全胜。然后删去这个,继续这样选。这样一定可以选出 \(24\) 个人,记为 \(A_1, A_2, \cdots, A_{24}\)。
下面证明这 \(24\) 个人一定是一条链(没有环)。假设有 \(A_1 \to A_2 \to \cdots \to A_k \to A_1\) 这样一个环,我们拿出 \(A_1\) 所在一个集合 \(\{A_1, B_1, B_2, \cdots, B_{26}\}\)。此时 \(A_1\) 战胜所有人。把前缀替换成 \(\{A_1, A_2, \cdots, A_k, B_{k}, \cdots, B_{26}\}\),此时集合里每个人都有战败人,不满足条件。
设 \(A_1 \to A_2 \to \cdots \to A_{24}\)。由一点竞赛图知识肯定知道 \(A_i\) 战胜 \(A_j\)(\(i < j\))。我们先拿 \(A_{24}\) 的一个集合 \(A_{24}, B_1, \cdots, B_{26}\),此时 \(B\) 中不可能有 \(A\) 中的人,否则就不是全胜了。然后换成 \(A_{24}, A_i, B_2, \cdots, B_{26}\),由于 \(A_i\) 打败 \(A_{24}\),且其它人不可能成为全胜,此时 \(A_i\) 全胜。也就能推出 \(A_i\) 战胜所有 \(B\)。也就得到 \(A_i\) 战胜除了 \(A_1\) 外的所有人。以此类推可以得到 \(A_1 \sim A_{24}\) 的得分分别为 \(26, 27, \cdots, 50\)。
用全负可以推出一些人的分数为 \(0, \sim, 23\)。剩下两个人只能是 \(24, 25\)。
所以分数全都不同。
物理好难
发现物理不会的太多了,可能在这里都写一遍会很浪费时间..?
看看情况


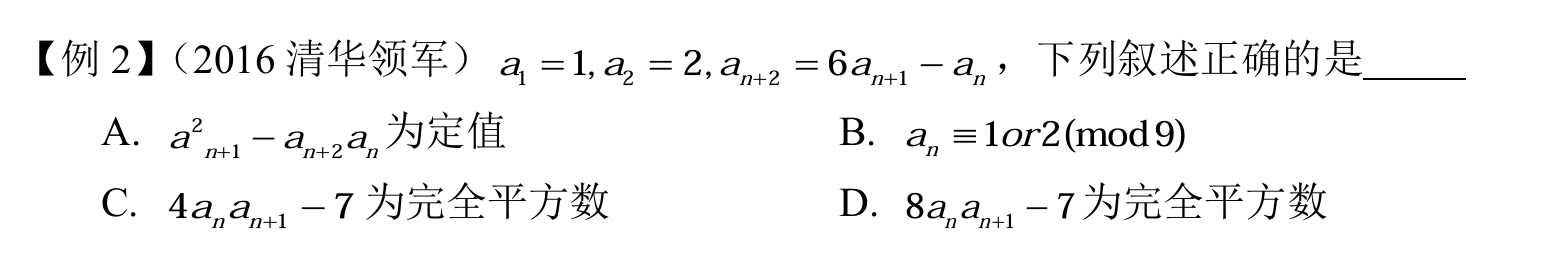
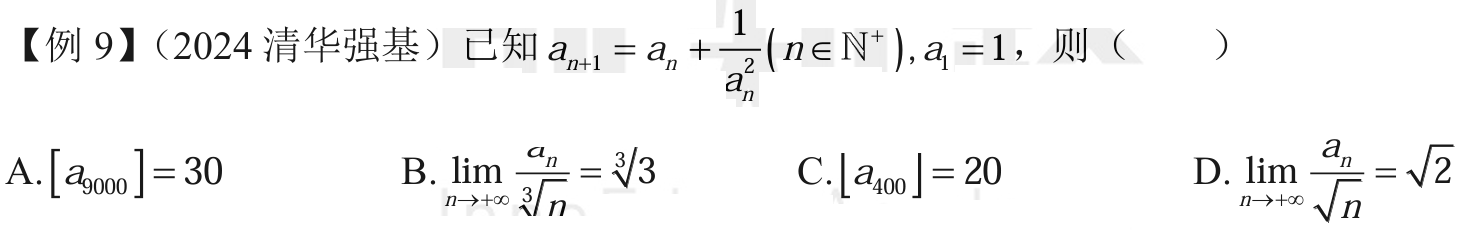







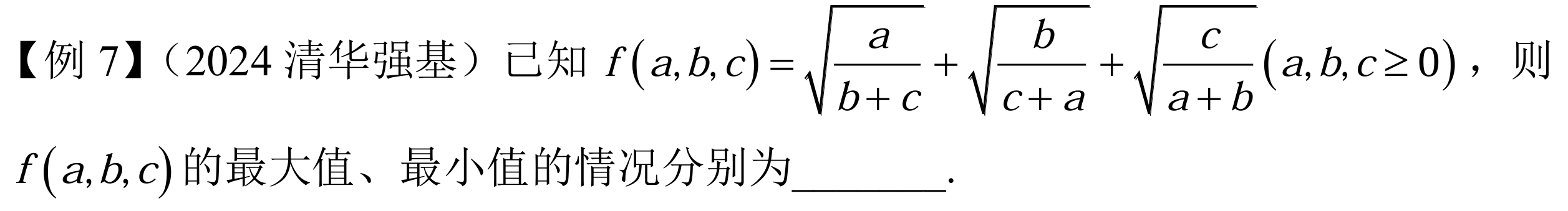




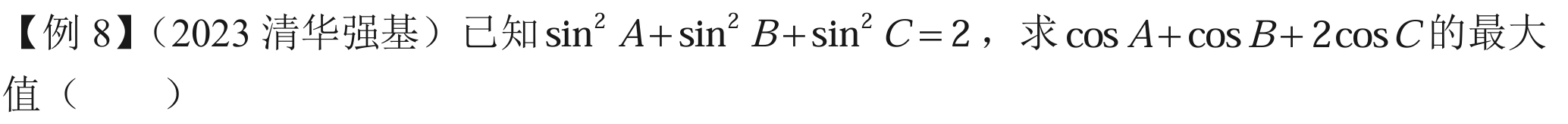




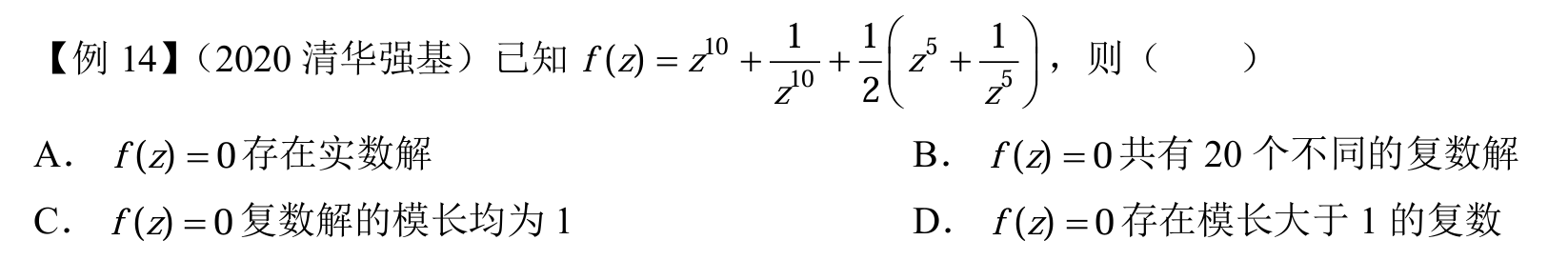
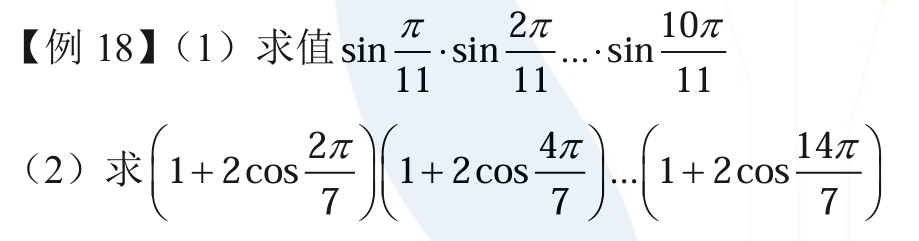





 浙公网安备 33010602011771号
浙公网安备 33010602011771号