高三鲜花 #4

大抵是高考前最后一篇鲜花了。

强基计划。

这其中有太多想说的事情了。

那天晚上我坐在床上，望着眼前的黑暗。可能只是坐着，面对着我的未来。

那天晚上我请假回家，和我妈彻夜长谈。飘渺的希望，在突如其来的万千变局之中，若现，若隐。

也许那个时代一去不复返了，也许一切将如故。

谁知道呢？在一万条毫无依据的证据建立的逻辑链下，一切的预测，距离真相又有多远呢？

也许是压垮骆驼的最后一根稻草。

---

一模考完之后，我听说了 tp 羟基政策出现变动的事情。

刚刚得知自己一模成绩的自己，本来想为自己约莫考上 650 而感到兴奋。可是从那一刻，我脑子里一片空白。

讲评，大概不是为我而讲的了。

我在笔记本上写下了一句话。

“大概是考上 650 了。可是还有什么用呢。”

---

可是我不想就此为止。

凭什么，在五年奥赛之后，在一年补上了所有文化课之后，一切的努力都最终让步于一个校测？

凭什么，同是奥塞生，他们就可以有出人优势，而留给我的只有一张冰冷的简章，冰冷地写着“你不配强基计划”？

我不甘心。

大约一个人的气愤达到了极点，就会转化成一种不知道从何而来的信念与勇气。

我在那行字下面写道：

“塞翁失马，焉知非福？？？”

---

冰冷的现实，无情的抽打着我。

“跟清华招生办打通过电话了，就是全国所有奥赛一起排名，不分科排。”

“前一百二全都是数奥和物奥怎么办？那我们也是只录取前一百二。”

---

人大概是不理性的吧。不知为何，这一切的残酷现实，却让我想再坚持。

这是一种捡漏心理吗？

这是对自己的前途规划负责的态度吗？

我不知道，但现在似乎只有一种想法驱动着我：

“凭什么？”

---

不就是校测吗，我把我高考的赛场再延长一个月行不行？？？

你考数学物理化学，我都没学过，那我现学行不行？？？

我他妈用了九个月从总分 483 学到了 650，现在你凭什么告诉我“对不起，你早该学数奥的”？？？

“信心和信念不是一个东西。”

我有没有信心考上，我不好说。

但是，奥赛，我辜负了太多人的期望。

现在，我至少不能辜负我六年来的期望了。

---

前几天，班主任把我们自己 100 天时写给自己的信，发给了我们。

希望到时候高考完的时候，我能把那封信带回来。那封信给了我一次沉重的打击，却又警醒了我最初的梦想。

这会是我的一个转折点吗？终将是重重谜团中的又一个环节，也许只能等待那一切的终结之时，看那水落石出吧。

大不了华科见，再大不了中山见。

---

也不能纯抒情和发牢骚吧，发一点学术内容。

众所周知阿氏圆：

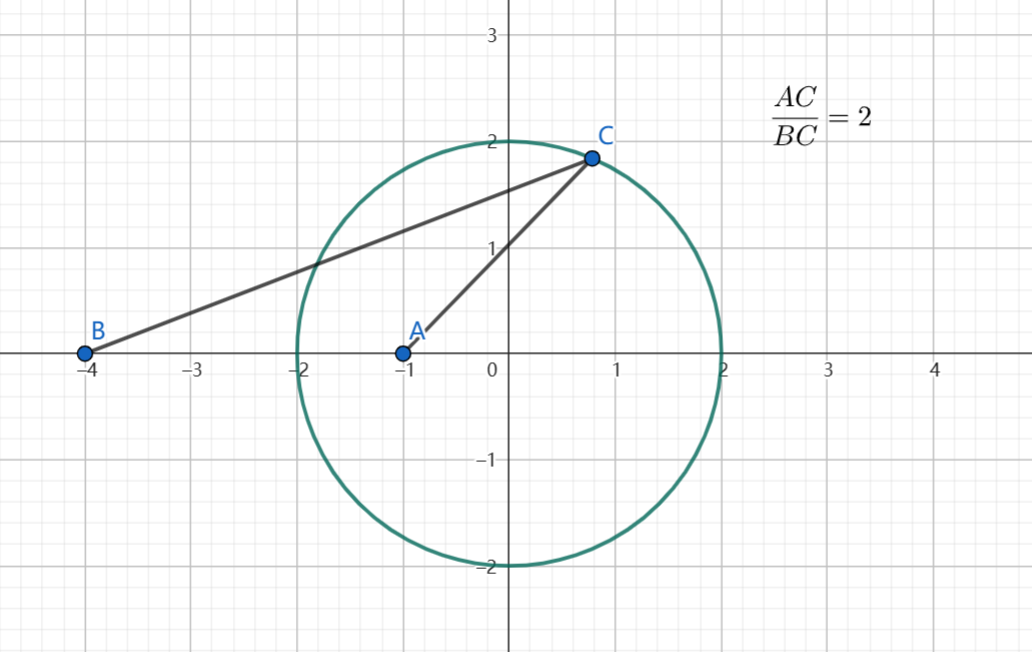
假如有两个点 \(A\) 和 \(B\)，动点 \(C\) 满足 \(\frac{BC}{AC} = \lambda\)，那么有 \(C\) 的轨迹是一个圆。

现在你看看这个图，是不是一股子 \(AO \times BO = r^2\) 的感觉？

证明一下：设这个圆为 \(x^2 + y^2 = r^2\)，\(A(\frac{r}{\lambda}, 0), B(r\lambda, 0), C(x, y)\)。

\[\begin{aligned} \frac{AP}{BP} &= \sqrt{\frac{(x-\frac{r}{\lambda})^2 + y^2}{(x-r\lambda)^2 + y^2}}\\ &= \sqrt{\frac{x^2 - \frac{2xr}{\lambda} + \frac{r^2}{\lambda^2} + y^2}{x^2 - 2xr \lambda + r^2\lambda^2 + y^2}}\\ &= \sqrt{\frac{r^2 - \frac{2xr}{\lambda} + \frac{r^2}{\lambda^2}}{r^2 - 2xr \lambda + r^2\lambda^2}}\\ &= \sqrt{\frac{r^2\lambda^2 - 2xr\lambda + r^2}{\lambda^2(r^2 - 2xr \lambda + r^2\lambda^2)}}\\ &= \frac{1}{\lambda} \end{aligned} \]

这不得不让我想起来圆锥曲线里面经常碰到的东西：伴侣点。

我碰到的大部分设题是：一个椭圆 \(\Gamma\)，过一个点 \(P\) 做直线交椭圆于 \(A, B\)，作 \(A\) 点关于 \(x\) 轴的对称点 \(C\)，直线 \(BC\) 过一个定点 \(Q\)。

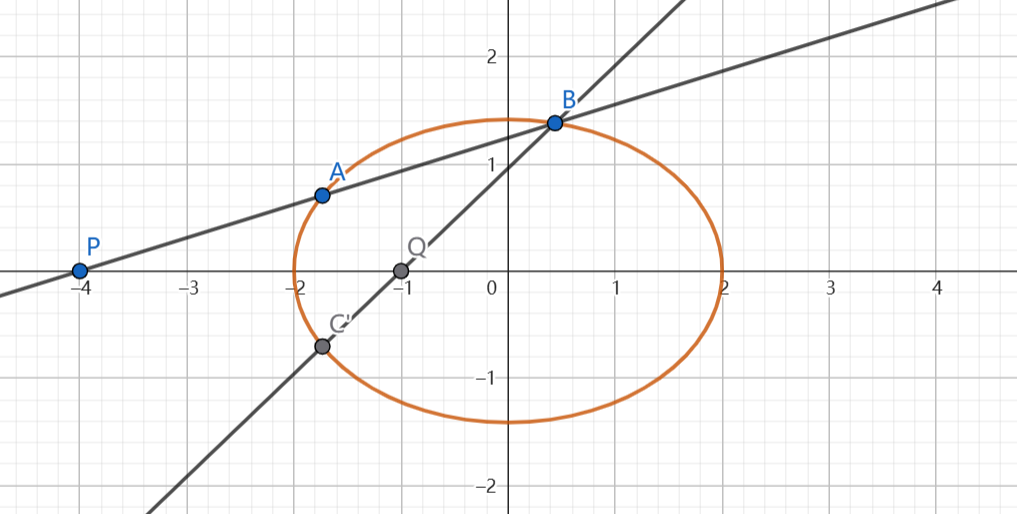
哎你发现这俩玩意是不是长的一模一样的！

证明懒得写了，我发现用 LaTeX 写圆锥曲线的过程有点折磨了。

反正你发现这个也有一个美丽的 \(OP \times OQ = a^2\)，所以你冥冥之中感觉这两个东西可能有联系。

由这种定义容易得出一个性质：\(PQ\) 是 \(\angle APC\) 的角平分线。

根据角平分线的性质，我们立即得到 \(\frac{PA}{AQ} = \frac{PB}{BQ}\)。

你发现阿氏圆其实就是这玩意把椭圆变成圆的情形阿。

并且因为圆比较好（？），所以还得出了一个 \(\frac{PA}{AQ} = \frac{PB}{BQ}\) 是一个定值的好性质。

或者反过来看，其实伴侣点就是把阿氏圆仿射变化了一下。所以如果想的话，其实是可以把这个东西仿射成圆，进而得到一些好性质？

但是仿射其实是不能保证边长之比的，所以这或许只是由角平分线得来的推论，因为仿射不改变角平分线的性质。所以这个发现似乎没啥用。

数学培优讲的题：

有四个正实数 \(a, b, c, d\)，满足 \(a\lt c\lt b\lt d\)，求 \(\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+d} + \frac{d}{d + a}\) 的取值范围。

我会基本不等式！

\[\begin{aligned} &\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+d} + \frac{d}{d + a}\\ \ge&\frac{16}{\frac{a+b}{a} + \frac{b+c}{b} + \frac{c+d}{c} + \frac{d+a}{d}}\\ =&\frac{16}{4 + \frac{b}{a} + \frac{c}{b} + \frac{d}{c} + \frac{a}{d}}\\ \le&\frac{16}{4 + 4\sqrt[4]{\frac{b}{a} \cdot \frac{c}{b} \cdot \frac{d}{c} \cdot \frac{a}{d}}}\\ =&\,2\\ \end{aligned} \]

哥你不等式方向反了。

伟大的数奥同学评价到：包反的。

教练我想学不等式。

\[\begin{aligned} &\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+d} + \frac{d}{d + a}\\ =&1 - \frac{b}{a+b} + \frac{b}{b+c} + 1 - \frac{d}{c+d} + \frac{d}{d + a}\\ =&2 + b (\frac{1}{c + b} - \frac{1}{a + b}) - d(\frac{1}{c + d} - \frac{1}{a + d})\\ \end{aligned} \]

哎美丽的相同形式。没看出来？构造个函数：\(f(x) = x(\frac{1}{c+x} - \frac{1}{a+x})\)，那原式子就是 \(2 + f(b) - f(d)\)。

现在看出来这个逼范围是为啥了吧！！！

\[\begin{aligned} f'(x) &= \frac{c}{(c+x)^2} - \frac{a}{(a+x)^2}\\ &=\frac{1}{c + \frac{x^2}{c} + 2x} - \frac{1}{a + \frac{x^2}{a} + 2x}\\ \end{aligned} \]

瞪一眼，\(c + \frac{x^2}{c}\) 在 \((0, x)\) 递减，条件是 \(a < c < b < d\)，也就是 \(a < c < x\)，那显然就有 \(f'(x) > 0\) 了。

那么原式子 \(2 + f(b) - f(d)\)，就有 \(b < d, f(b) < f(d), 2 + f(b) - f(d) < 2\) 了。

哎呀恭喜你证明完一半了，范围另一边咋求阿？

可以暴力一点，直接让 \(f(b)\) 取最小，\(f(d)\) 取最大。也就是让 \(b \to c, d \to +\infty\)。

就有 \(2 + f(b) - f(d) > 2 + \frac{1}{2} - \frac{c}{a+c}\)。

再大力让 \(a \to 0\)，哎得到 \(2 + f(b) - f(d) > \frac{3}{2}\)，大功告成了。最后范围就是 \((\frac{3}{2}, 2)\)。

哲人告诉我们：一边可能用不等式，另一边大概率就是令两个极限，剩下的相等。

额这是暴论，其实我也没想清楚啥时候配速法是真正有用的。如果涉及轨迹和时间相关问题可能需要用一下，不过感觉大部分情况都是可以水平竖直动量定理解决掉的。

我爱分方向动量定理！！！11

有没有人能教教我这个阿。