数学和CNN里面的卷积和互相关

卷积和互相关

nndl上CNN这章的互相关讲的比较晦涩，简单辨析一下书上的互相关

A.1

数学意义上的卷积就是将卷积核进行翻转之后再进行我们熟悉CNN上的卷积运算

同时互相关就是不将卷积核翻转直接CNN卷积运算

说到这里就明白了，做如下总结

• \(数学上的互相关=CNN卷积\)
• $数学上的卷积 = CNN扣一个翻转卷积核 $

A.2

翻转卷积核的运算方式有很多

比较经典的就是使用高中选修课本上的旋转矩阵，我们也有更加直观的方式

参考：卷积核翻转方法-CSDN博客

• 沿核中心旋转（顺或逆)\(180^{\circ}\)
• 先后沿主副对角线翻转矩阵
• 先后沿行列中心进行翻转

简单计算验证

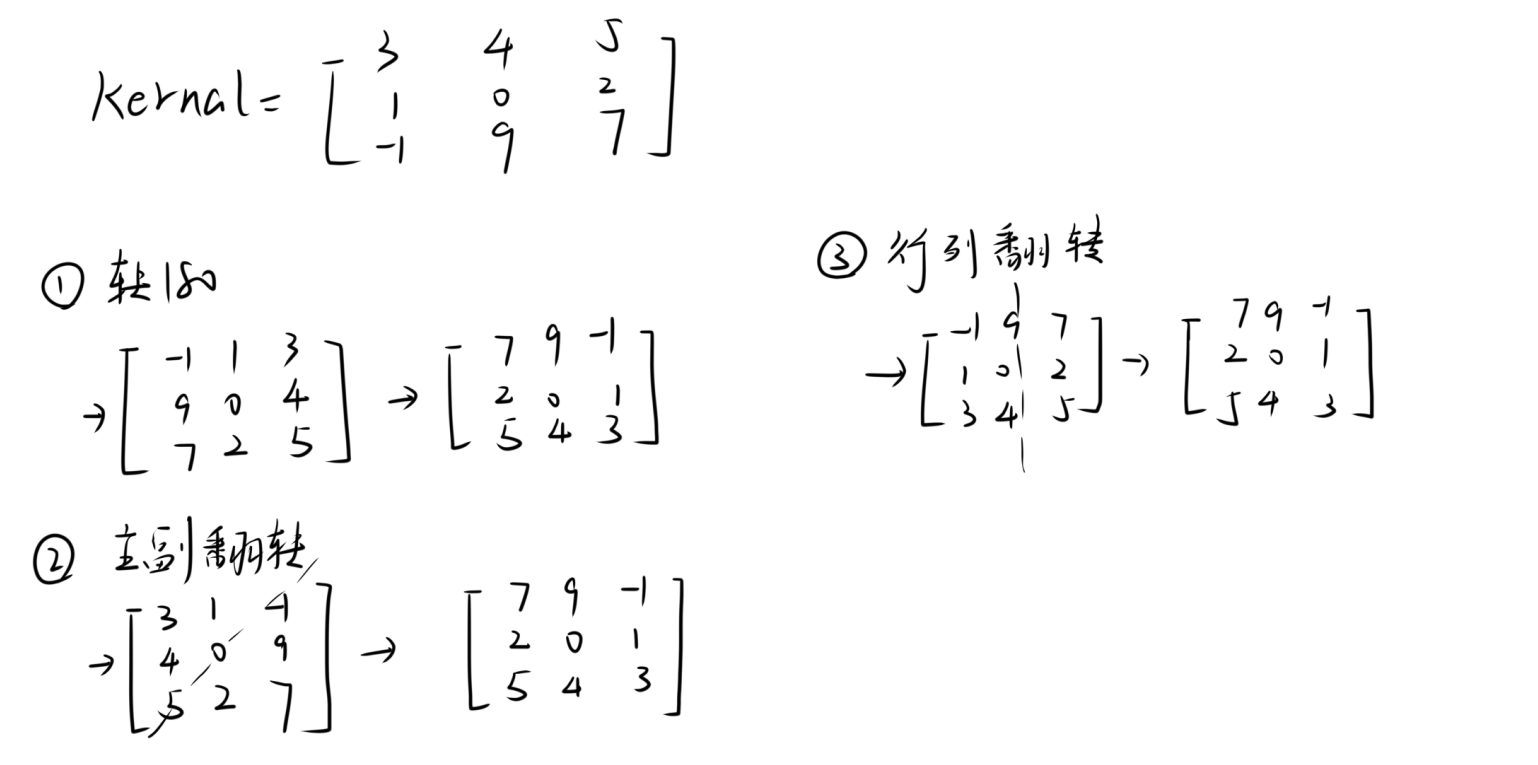
！注：上面第一个运算是顺时针，采用逆时针结果相同

B

Bpart总结

其实在CNN中卷积就是数学里面的互相关。
我们也不关心翻转，因为不翻转就能很好的解决CV的一些问题。
通常我们在CNN或者DL中说的卷积默认互相关，如果需要翻转卷积核我们会特别指出。