NOIP 2016 蚯蚓
题目链接https://www.luogu.com.cn/problem/P2827
不知道为啥出题人跟蚯蚓过不去
分析
这道题我看到后第一感觉是模拟,因为它的输出很有特点,既有过程也有最终答案,所以不可能会有什么公式之类的,那怎么模拟呢?这个蚯蚓长度是动态更新的,所以我们可以考虑动态维护它的大小,用一个优先队列就行,当然,最开始我觉得能过,因为某OJ上边写的是十秒,(其实后来算了算十秒也是过不了的),好吧你不信的话现在来算一算,二叉堆的时间复杂度是\(O(NlogN)\),放到这题就是\(MlogN\),最大值是多少呢?\(7*10^6*log_210^5\),\(log_210^5\)大概是17左右,7*17是119,总的时间复杂度最低也是\(1.19*10^8\),然而因为\(STL\)自带大常数,所以最多跑到\(10^7\)就会T,故\(10s\)也不够用,那手写堆呢?感觉应该也不行,因为上述只是最低时间复杂度,事实上因为还有输入输出啥的,尤其这题输入输出比较多,也会T掉。
我们先不考虑T掉的问题,这个可以优化,先想想暴力怎么做。其实也很简单,就每次从堆里揪出一只蚯蚓来劈成两半然后再加进去就行,那蚯蚓的自然生长怎么办??也很简单,只有这一只蚯蚓不需要生长,所以我定义一个\(sum\)变量记录蚯蚓的生长,每次让它加上生长长度,把蚯蚓劈完后减去生长长度再扔进去就行,这样就等价于它没有生长。代码如下TLE
#include<cstdio>
#include<queue>
#include<cmath>
using namespace std;
priority_queue<int > que;
int main(){
int n,m,q,u,v,t;
int sum=0;
scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);
for(int i=1;i<=n;i++){
int a;
scanf("%d",&a);
que.push(a);
}
double p=(double)u/v;
for(int i=1;i<=m;i++){
if(i%t==0)
printf("%d ",que.top()+sum);
u=que.top()+sum;que.pop();
int now=(double)u*p;que.push(now-q-sum);que.push(u-now-sum-q);
sum+=q;
}
printf("\n");
int cnt=0;
while(!que.empty()){
cnt++;
if(cnt%t==0)printf("%d ",que.top()+sum);
que.pop();
}
}
优化
优化说起来也很简单,就是不太好想到。对于这种需要重复排序的问题,很可能存在某种单调性,可以使\(O(logN)\)的维护最大值变成\(O(1)\)的,这道题就是。
存在什么单调性呢?假设最开始的每只蚯蚓排序后从大到小依次长\(x_i\),那么我根据题意肯定是从\(x_1\)开始切,切完之后,假设\(\lfloor px\rfloor\)为\(l\),另一半为\(r\),那么一定会从\(l_1\)开始单调递减,\(r\)同理,也就是说如果我建三个队列来分别维护初始,\(l\),\(r\),这三个队列都是单调的,即每次查询比较队首即可。下面来证明一下:
先证明\(l\)是单调的,假设\(i<j\),设\(c\)表示蚯蚓增加的长度,根据初始的单调性,\(x_i>=x_j\),所以\(\lfloor px_i\rfloor>=\lfloor px_j\rfloor\)
继而有\(\lfloor px_i+c\rfloor>=\lfloor p(x_j+c)\rfloor\)因为\(p\)小于1,所以\(c>pc\)。
因为在下取整号里边的是可以拿出来的,这一点是显然的,拿出来不会改变不等号方向。所以\(\lfloor px_i\rfloor+c>=\lfloor p(x_j+c)\rfloor\)
易得\(\lfloor px_i\rfloor>=\lfloor p(x_j+c)\rfloor-c\),这时你会发现不等号左边就是\(l_i\)右边是\(l_j\),故原式得证。
接下来证明\(r\)是单调的,其实两者差不多,都用到了放缩的思想。
因为\(x_i>=x_j\)所以\((1-p)x_i>=(1-p)x_j即x_i-px_i>=x_j-px_j\)
得,\(\lceil x_i-px_i\rceil>=\lceil x_j-px_j\rceil\)注意这里是上取整
上取整号拆开需要稍微作一下变化,即\(x_i-\lfloor px_i\rfloor>=x_j-\lfloor px_j\rfloor\)
然后可以得到,\(x_i-\lfloor px_i\rfloor>=x_j+c-\lfloor px_j\rfloor-c\)
到这里会发现这个式子很接近于\(r\)了,只差最后一步放缩,因为减去一个正数不会让一个数更大,所以我在右边减去一个数不会让不等号方向改变
于是可得\(x_i-\lfloor px_i\rfloor>=x_j+c-\lfloor p(x_j-c)\rfloor-c\)
故有\(r_i>=r_j\),证毕。
细节
1.longlong用不用
肯定是不需要的,假设最开始都是最长\(10^8\),每秒长\(200\),最多也就长\(7*10^6*200\)即\(14*10^8\),二者相加是\(15*10^8\),
而\(int\)是\(21*10^8\),所以不会爆。
2.最大值的取法
因为上边说了,最大可到\(15*10^8\),所以初始化INF不能用\(0x3f3f3f3f\),把3换成7就行。
3.还跟longlong有关系
那为啥有的代码没用longlong就错,用了就对呢?主要是一个地方
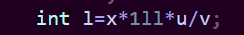
这俩相乘的时候可能会爆longlong,当然你预处理那个分数也就自行忽视。
#include<cstdio>
#include<algorithm>
const int N=7e6+10,INF=0x7f7f7f7f;
using namespace std;
int q1[N],tt1,hh1,q2[N],tt2=-1,hh2,q3[N],tt3=-1,hh3;
int sum;
bool cmp(int a,int b){
return a>b;
}
int find(){
int x=-INF;
if(hh1<=tt1)x=max(x,q1[hh1]);
if(hh2<=tt2)x=max(x,q2[hh2]);
if(hh3<=tt3)x=max(x,q3[hh3]);
if(hh1<=tt1&&x==q1[hh1])hh1++;
else if(hh2<=tt2&&x==q2[hh2])hh2++;
else if(hh3<=tt3&&x==q3[hh3])hh3++;
return x;
}
int main(){
int n,m,q,u,v,t;
scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);
for(int i=0;i<n;i++)
scanf("%d",&q1[i]);
tt1=n-1;
sort(q1,q1+n,cmp);
for(int i=1;i<=m;i++){
int x=find();
x+=sum;
int l=x*1ll*u/v;
int r=x-l;
sum+=q;
q2[++tt2]=l-sum;
q3[++tt3]=r-sum;
if(i%t==0)printf("%d ",x);
}
printf("\n");
for(int i=1;i<=n+m;i++){
int x=find();
if(i%t==0)printf("%d ",x+sum);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号