【组合数学 思维题】10.6种树

感谢学弟贡献的精彩人类智慧

题目大意

计数$1 \le k \le n$个节点的除叶子节点外所有节点均有两个儿子，且任意叶子节点到根的左偏距离$\le m$的二叉树方案数.

$n,m \le 5000$

---

题目分析

做法一：带性质的序列转化

考虑一下这些叶子的左偏距离有没有什么性质

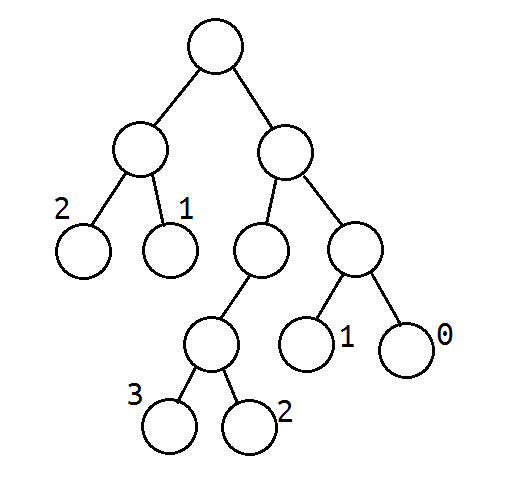
首先把叶子从左到右写成一个序列。初看上去相邻两个权值的变化没有什么规律，但是仔细思考一下就会发现因为每一个左叶子都有对应的右叶子，因此对相邻的元素有关系$w_L \le w_R+1$。并且这样构造出来的序列是和合法的二叉树一一对应的。

于是接下来dp构造这个序列。$f[i][j]$表示构造完了$1\cdots i$，现在$i$位置权值为$j$的合法方案数。最终的答案就是$f[i][0]$.

#include<bits/stdc++.h>
#define MO 998244353
const int maxn = 5035;

int n,m,f[maxn][maxn],sum[maxn];

int main()
{
    scanf("%d%d",&m,&n), --m;
    for (int i=0; i<=m; i++) f[1][i] = 1;
    for (int i=2; i<=n; i++)
    {
        for (int j=1; j<=m; j++)
            sum[j] = (sum[j-1]+f[i-1][j])%MO;
        for (int j=0; j<=m; j++)
            f[i][j] = (f[i][j]+sum[std::min(m, j+1)])%MO;
    }
    for (int i=1; i<=n; i++) printf("%d\n",f[i][0]);
    return 0;
}

 

做法二：类比卡特兰数模型

考虑建模转化这一个问题

首先如果一点附加条件都没有，这即是二叉树的计数问题，应当要想到卡特兰数。

那我们就类比卡特兰数的平面直角坐标系带限制走路问题来考虑。

这是类似dfs树的一个优先走左儿子的过程，定义每一次向左儿子（并非只对左叶子）走就是在坐标系上走$\texttt{(1,1)}$的一步；从左儿子回溯向上就是在坐标系上走$\texttt{(0,-1)}$的一步。

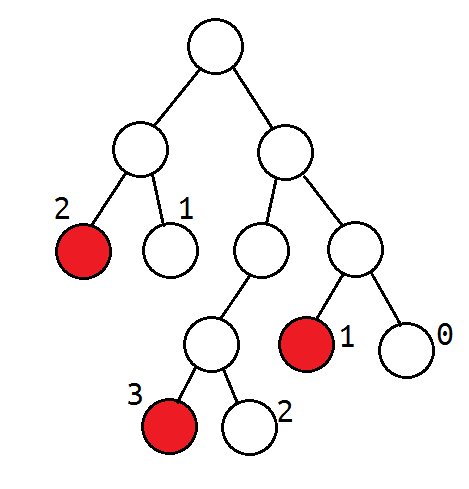
以上面这棵树为例，构造出来的坐标系是这样的。

得益于这棵“左右儿子对应存在”的二叉树特殊性质，拥有$n$个叶子节点的树中恰好会有$n$个左儿子，也就是说坐标系上最后的终点是$\texttt{(n,0)}$.而图像里每一个拐点即对应有着极大值的左叶子。

这个构造的性质非常好，由此我们发现了“左偏距离$\le m$”的所有方案即和“图像上所有拐点纵坐标$<m$”的情况一一对应。所以之后便可以朴素而直观地dp处理$f[i][0]$表示到达$\texttt{(i,0)}$的方案数量。

#include<bits/stdc++.h>
#define MO 998244353
const int maxn = 5035;

int m,n,f[maxn][maxn];

int main()
{
    scanf("%d%d",&m,&n), --m;
    f[0][0] = 1;
    for (int i=1; i<=n; i++)
        for (int j=m; j>=0; j--)
        {
            int c = 0;
            if (j) c += f[i-1][j-1];
            if (j!=m) c += f[i][j+1];
            f[i][j] = (f[i][j]+c)%MO;
        }
    for (int i=0; i<n; i++) printf("%d\n",f[i][0]);
    return 0;
}

 

 

 

END