【计数】cf223C. Partial Sums

考试时候遇到这种题只会找规律

You've got an array a, consisting of n integers. The array elements are indexed from 1 to n. Let's determine a two step operation like that:

1. First we build by the array a an array s of partial sums, consisting of n elements. Element number i (1 ≤ i ≤ n) of array s equals 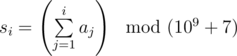. The operation x mod y means that we take the remainder of the division of number x by number y.
2. Then we write the contents of the array s to the array a. Element number i (1 ≤ i ≤ n) of the array s becomes the i-th element of the array a (ai = si).

You task is to find array a after exactly k described operations are applied.

Input

The first line contains two space-separated integers n and k (1 ≤ n ≤ 2000, 0 ≤ k ≤ 109). The next line contains n space-separated integers a1, a2, ..., an — elements of the array a (0 ≤ ai ≤ 109).

Output

Print n integers  — elements of the array a after the operations are applied to it. Print the elements in the order of increasing of their indexes in the array a. Separate the printed numbers by spaces.

---

题目分析

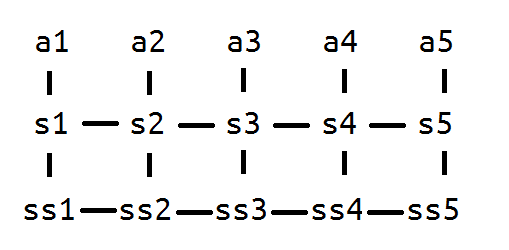
可以从矩阵乘法开始想起，考虑转移矩阵，发现其主对角线下方全为0、元素按照次对角线对称。

或者就是找规律

3.16upd：

总觉得一个经典模型不应该用找规律这么假的方式随随便便搞掉吧……

网上的题解都是打表找规律 | 矩乘找规律 | dp找规律……

来自ZZK的新的理解方式：$a_i$的贡献也就是它走到$s^p_j$的方案数量。

#include<bits/stdc++.h>
#define MO 1000000007
const int maxn = 2035;

int n,k,a[maxn],b[maxn],inv[maxn],fac[maxn],pre[maxn];

void init()
{
    fac[0] = fac[1] = inv[0] = inv[1] = 1;
    for (int i=2; i<=n; i++)
        fac[i] = 1ll*fac[i-1]*i%MO, 
        inv[i] = MO-1ll*(MO/i)*inv[MO%i]%MO;
    pre[0] = 1;
    for (int i=1; i<=n; i++)
        pre[i] = 1ll*pre[i-1]*(k%MO+i-1)%MO*inv[i]%MO;
}
int main()
{
    scanf("%d%d",&n,&k);
    for (int i=1; i<=n; i++) scanf("%d",&a[i]), b[i] = a[i];
    if (k){
        init();
        for (int i=1; i<=n; i++)
        {
            b[i] = 0;
            for (int j=1; j<=i; j++)
                b[i] = 1ll*(b[i]+1ll*pre[i-j]*a[j]%MO)%MO;
        }
    }
    for (int i=1; i<=n; i++) printf("%d ",b[i]);
    return 0;
}

 

 

END