初涉线性基
线性基是什么
线性基最初设计是应用于向量运算的。而异或恰好满足向量的性质(将每个数以二进制看做一组向量),因此线性基广泛引用于异或问题,同时具有很多巧妙的性质。
简单的来说,线性基处理的对象是一组数$\{a_i\}$,构造出一组数$\{b_i\}$,使得它们异或出的值域相同。而$b_i$满足其最高位是第$i$位。这个基础性质保证了很多其他很好的性质。
构造线性基模板:
1 for (int i=1; i<=n; i++) 2 for (int j=60, chk=0; j>=0&&!chk; j--) 3 if (a[i]>>j){ 4 if (!p[j]) p[j] = a[i], chk = 1; 5 else a[i] ^= p[j]; 6 }
其中$p[]$是线性基
一些例题
【最大异或和】luoguP3812 【模板】线性基
题目描述
给定n个整数(数字可能重复),求在这些数中选取任意个,使得他们的异或和最大。
输入输出格式
输入格式:
第一行一个数n,表示元素个数
接下来一行n个数
输出格式:
仅一行,表示答案。
题目分析

1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 103; 4 5 int n; 6 ll p[maxn],a[maxn],ans; 7 8 ll read() 9 { 10 char ch = getchar(); 11 ll num = 0, fl = 1; 12 for (; !isdigit(ch); ch=getchar()) 13 if (ch=='-') fl = -1; 14 for (; isdigit(ch); ch=getchar()) 15 num = (num<<1)+(num<<3)+ch-48; 16 return num*fl; 17 } 18 int main() 19 { 20 n = read(); 21 for (int i=1; i<=n; i++) a[i] = read(); 22 for (int i=1; i<=n; i++) 23 for (int j=50, chk=0; j>=0&&!chk; j--) 24 if (a[i]>>j){ 25 if (!p[j]) p[j] = a[i], chk = 1; 26 else a[i] ^= p[j]; 27 } 28 for (int i=50; i>=0; i--) 29 if ((ans^p[i]) > ans) ans ^= p[i]; 30 printf("%lld\n",ans); 31 return 0; 32 }
【k大异或和】hdu3949XOR
Problem Description
XOR is a kind of bit operator, we define that as follow: for two binary base number A and B, let C=A XOR B, then for each bit of C, we can get its value by check the digit of corresponding position in A and B. And for each digit, 1 XOR 1 = 0, 1 XOR 0 = 1, 0 XOR 1 = 1, 0 XOR 0 = 0. And we simply write this operator as ^, like 3 ^ 1 = 2,4 ^ 3 = 7. XOR is an amazing operator and this is a question about XOR. We can choose several numbers and do XOR operatorion to them one by one, then we get another number. For example, if we choose 2,3 and 4, we can get 2^3^4=5. Now, you are given N numbers, and you can choose some of them(even a single number) to do XOR on them, and you can get many different numbers. Now I want you tell me which number is the K-th smallest number among them.
Input
First line of the input is a single integer T(T<=30), indicates there are T test cases.
For each test case, the first line is an integer N(1<=N<=10000), the number of numbers below. The second line contains N integers (each number is between 1 and 10^18). The third line is a number Q(1<=Q<=10000), the number of queries. The fourth line contains Q numbers(each number is between 1 and 10^18) K1,K2,......KQ.
Output
For each test case,first output Case #C: in a single line,C means the number of the test case which is from 1 to T. Then for each query, you should output a single line contains the Ki-th smallest number in them, if there are less than Ki different numbers, output -1.
题目分析
考虑重构线性基,使它具有更好的性质:使$p_i$成为整个线性基内,唯一在$i$位为1的数字。
这样做的好处在于,自低位向高位异或过程中,能保证结果是递增的。这样一来,就可以把k二进制分解,来构造k大的数。
正确性的证明,和线性基的插入其实是一个道理。因为在线性基自身异或的过程中,它的张成并不改变;并且,线性基保证了任意数字异或出的结果不为0.
题外话:我好像又忘了hdu不支持bits库。
1 #include<cstdio> 2 #include<cctype> 3 #include<cstring> 4 typedef long long ll; 5 6 int T,n,q,sc,legal; 7 ll p[63],pos,ans; 8 9 ll read() 10 { 11 char ch = getchar(); 12 ll num = 0, fl = 1; 13 for (; !isdigit(ch); ch=getchar()) 14 if (ch=='-') fl = -1; 15 for (; isdigit(ch); ch=getchar()) 16 num = (num<<1)+(num<<3)+ch-48; 17 return num*fl; 18 } 19 void insert(ll num) 20 { 21 for (int i=60, chk=0; i>=0&&!chk; i--) 22 if (num>>i){ 23 if (p[i]) num ^= p[i]; 24 else p[i] = num, chk = 1, ++legal; 25 } 26 } 27 void rebuild() 28 { 29 for (int i=60; i>=0; i--) 30 if (p[i]) for (int j=i+1; j<=60; j++) 31 if ((p[j]>>i)&1) p[j] ^= p[i]; //这一步就是重构线性基,使其具有更好性质 32 for (int i=0, j=-1; i<=60; i++) 33 if (p[i]) p[++j] = p[i]; //这一步处理是为了将k二进制分解时候方便起见 34 } 35 int main() 36 { 37 for (T=read(); T; --T, legal=0) 38 { 39 memset(p, 0, sizeof p); 40 printf("Case #%d:\n",++sc); 41 n=read(), legal=0; 42 for (int i=1; i<=n; i++) insert(read()); 43 rebuild(); 44 for (q=read(); q; q--) 45 { 46 pos = read(); 47 if (n!=legal) --pos; //若legal!=n,说明0可被表示 48 if (pos >= (1ll<<legal)) puts("-1");//线性基任意数字异或不为0,所以共有2^legal种数 49 else{ 50 ans = 0; 51 for (int i=0; i<=60; i++) 52 if ((pos>>i)&1) ans ^= p[i]; //将k二进制分解处理ans 53 printf("%lld\n",ans); 54 } 55 } 56 } 57 return 0; 58 }
【最大权值和】bzoj2460: [BeiJing2011]元素
Description
相传,在远古时期,位于西方大陆的 Magic Land 上,人们已经掌握了用魔
法矿石炼制法杖的技术。那时人们就认识到,一个法杖的法力取决于使用的矿石。
一般地,矿石越多则法力越强,但物极必反:有时,人们为了获取更强的法力而
使用了很多矿石,却在炼制过程中发现魔法矿石全部消失了,从而无法炼制
出法杖,这个现象被称为“魔法抵消” 。特别地,如果在炼制过程中使用超过
一块同一种矿石,那么一定会发生“魔法抵消”。
后来,随着人们认知水平的提高,这个现象得到了很好的解释。经过了大量
的实验后,著名法师 Dmitri 发现:如果给现在发现的每一种矿石进行合理的编
号(编号为正整数,称为该矿石的元素序号),那么,一个矿石组合会产生“魔
法抵消”当且仅当存在一个非空子集,那些矿石的元素序号按位异或起来
为零。 (如果你不清楚什么是异或,请参见下一页的名词解释。 )例如,使用两
个同样的矿石必将发生“魔法抵消”,因为这两种矿石的元素序号相同,异或起
来为零。
并且人们有了测定魔力的有效途径,已经知道了:合成出来的法杖的魔力
等于每一种矿石的法力之和。人们已经测定了现今发现的所有矿石的法力值,
并且通过实验推算出每一种矿石的元素序号。
现在,给定你以上的矿石信息,请你来计算一下当时可以炼制出的法杖最多
有多大的魔力。
Input
第一行包含一个正整数N,表示矿石的种类数。
接下来 N行,每行两个正整数Numberi 和 Magici,表示这种矿石的元素序号
和魔力值。
Output
仅包一行,一个整数:最大的魔力值
题目分析
题目要求异或出的集合不为0,这用线性基可以保证;而要求权值最大,则可以贪心地从大到小插入元素。
就具体而言,为保证贪心过程异或出的数不为0,需要检验它是否能插入已有的线性基。如果无法插入,说明已选入的数能异或出它,因此依靠贪心原则排除此数。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 1035; 4 5 int n,id[maxn],w[maxn]; 6 ll a[maxn],p[maxn],ans; 7 8 ll read() 9 { 10 char ch = getchar(); 11 ll num = 0, fl = 1; 12 for (; !isdigit(ch); ch=getchar()) 13 if (ch=='-') fl = -1; 14 for (; isdigit(ch); ch=getchar()) 15 num = (num<<1)+(num<<3)+ch-48; 16 return num*fl; 17 } 18 bool cmp(int a, int b){return w[a] > w[b];} 19 int main() 20 { 21 n = read(); 22 for (int i=1; i<=n; i++) 23 a[i] = read(), w[i] = read(), id[i] = i; 24 std::sort(id+1, id+n+1, cmp); 25 for (int ix=1; ix<=n; ix++) 26 { 27 int i = id[ix], chk = 0; 28 for (int j=60; j>=0&&!chk; j--) 29 if (a[i]>>j){ 30 if (!p[j]) p[j] = a[i], chk = 1; 31 else a[i] ^= p[j]; 32 } 33 if (chk) ans += w[i]; 34 } 35 printf("%lld\n",ans); 36 return 0; 37 }
【无向图最大路径】bzoj2115: [Wc2011] Xor
Description

Input
第一行包含两个整数N和 M, 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边,每行三个整数Si,Ti ,Di,表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。
Output
仅包含一个整数,表示最大的XOR和(十进制结果),注意输出后加换行回车。
题目分析
这题允许多次经过同一个边或点,所以会发现,最优的路径会是一条主路连出若干个环。
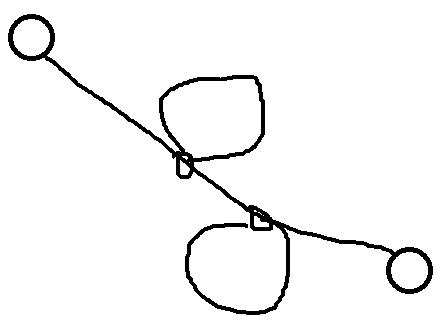
这一类图的问题大都可以考虑成树边+非树边的形式。
先任意构造一个dfs树,再来考虑图中所有的环。下面为了方便起见,把最早处理出的1-n路径称为“原始路径”。
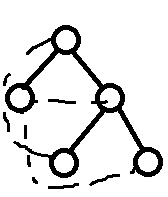
奇偶环的区别在于,选奇环意味着原始路径会成为链+环的形式;选偶环说明原始路径会变成另一条链。这意味着,通过任意一条原始路径,再异或一定数量的环,就能构造出最优路径。
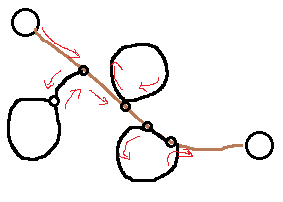
(上图中棕色表示原始路径,黑圈表示选取的环,红箭头表示最优路径)
因此,如果将所有环都抠出来,就相当于变成了上一个问题:“选出一些数字,使得它们的异或和最大”。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 50000; 4 const int maxm = 200035; 5 6 struct Edge 7 { 8 int y; 9 ll val; 10 Edge(int a=0, ll b=0):y(a),val(b){} 11 }edges[maxm]; 12 int n,m; 13 bool vis[maxn]; 14 ll w[maxn],p[65],ans; 15 int edgeTot,head[maxn],nxt[maxm]; 16 17 ll read() 18 { 19 char ch = getchar(); 20 ll num = 0, fl = 1; 21 for (; !isdigit(ch); ch=getchar()) 22 if (ch=='-') fl = -1; 23 for (; isdigit(ch); ch=getchar()) 24 num = (num<<1)+(num<<3)+ch-48; 25 return num*fl; 26 } 27 void addedge() 28 { 29 int u = read(), v = read(); 30 ll c = read(); 31 edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot; 32 edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot; 33 } 34 void insert(ll num) 35 { 36 for (int j=60, chk=0; j>=0&&!chk; j--) 37 if ((num>>j)&1){ 38 if (!p[j]) p[j] = num, chk = 1; 39 else num ^= p[j]; 40 } 41 } 42 void dfs(int x, ll c) 43 { 44 vis[x] = 1, w[x] = c; 45 for (int i=head[x]; i!=-1; i=nxt[i]) 46 if (!vis[edges[i].y]) dfs(edges[i].y, c^edges[i].val); 47 else insert(c^w[edges[i].y]^edges[i].val); 48 } 49 int main() 50 { 51 memset(head, -1, sizeof head); 52 n = read(), m = read(); 53 for (int i=1; i<=m; i++) addedge(); 54 dfs(1, 0), ans = w[n]; 56 for (int i=60; i>=0; i--) 57 ans = std::max(ans, ans^p[i]); 58 printf("%lld\n",ans); 59 return 0; 60 }
【无向图路径总和】cf724G. Xor-matic Number of the Graph
You are given an undirected graph, constisting of n vertices and m edges. Each edge of the graph has some non-negative integer written on it.
Let's call a triple (u, v, s) interesting, if $1 ≤ u < v ≤ n$ and there is a path (possibly non-simple, i.e. it can visit the same vertices and edges multiple times) between vertices u and v such that xor of all numbers written on the edges of this path is equal to s. When we compute the value s for some path, each edge is counted in xor as many times, as it appear on this path. It's not hard to prove that there are finite number of such triples.
Calculate the sum over modulo $10^9 + 7$ of the values of s over all interesting triples.
Input
The first line of the input contains two integers n and m $(1 ≤ n ≤ 100 000, 0 ≤ m ≤ 200 000)$ — numbers of vertices and edges in the given graph.
The follow m lines contain three integers ui, vi and ti $(1 ≤ ui, vi ≤ n, 0 ≤ ti ≤ 10^{18}, ui ≠ vi)$ — vertices connected by the edge and integer written on it. It is guaranteed that graph doesn't contain self-loops and multiple edges.
Output
Print the single integer, equal to the described sum over modulo $10^9 + 7$.
题目大意
求无向图中所有异或路径和的代数和,长度相同的路径只计入答案一次。$n<1e5$
题目分析
将图->树考虑;下面的讨论基于同一个连通块内。
如果是树,那么按位$t$考虑。先预处理出随意一个起点到任意点的异或和路径长度,那么$x$到$y$的路径就是$dis[x] \, xor \,dis[y]$。记$sum[0/1]$分别为在$t$位上,$dis_i$为0/1的点的数目,那么答案就是$sum[0]*sum[1]*2^t$。
图就相当于是树加上一些环边。照上一题的套路,先把环都抠出来放进线性基里,并注意到原树上的路径xor任意一些环都是图上的路径。于是可以把树的答案先统计出来,再考虑线性基对答案贡献。
记$\text{legal}$为线性基内的合法元素数量;$\text{used}$表示每一位是否能够被线性基表示。那么对于一个位$t$,若$\text{(used>>t&1)==1}$即$t$位可被表示,此时有两种情况会对$t$位产生贡献:1.和树边一样的情况,sum[0]与sum[1]匹配;2.因为有环边存在,且位$t$可被表示,所以可以sum[0]、sum[1]各自自身匹配使此位为0,再由线性基提供一种此位为1的情况。而对于一个位$t$,当$\text{(used>>t&1)==0}$即$t$位不可被表示的时候,就只有sum[0]和sum[1]匹配才能够产生贡献。
那么统计贡献的思路已经有了,如何具体处理第一种贡献呢?换句话,如何计数线性基使特定位$t$为1的方案数?
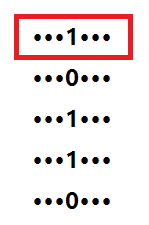
可以这么理解:线性基在$t$位有如上$legal=5$个数。那么将这位为1的其中一个数强行取出,考虑其他$legal-1$个数。其他数的组合一共有$2^{legal-1}$种,而且结果非零即一。如果结果为1,那正好,不需要额外处理;如果结果为0,那么可以使用强行取出的这个数来保证结果为1,。这样看来,所有的$2^{legal-1}$种情况就正好是线性基使$t$位为1的充要情况。
本题挂掉的小细节:
- dis[]和线性基p[]居然忘开long long了
- maxn是1e5,maxm是4e5
- int类型>>33==int类型>>(33%32)!
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int MO = 1000000007; 4 const int maxn = 100035; 5 const int maxm = 400035; 6 7 struct Edge 8 { 9 int y; 10 ll val; 11 Edge(int a=0, ll b=0):y(a),val(b) {} 12 }edges[maxm]; 13 int n,m,sum[3],legal; 14 int edgeTot,head[maxn],nxt[maxm]; 15 int cnt,stk[maxn]; 16 ll ans,used,pwr[65],dis[maxn],p[65]; 17 18 ll read() 19 { 20 char ch = getchar(); 21 ll num = 0, fl = 1; 22 for (; !isdigit(ch); ch=getchar()) 23 if (ch=='-') fl = -1; 24 for (; isdigit(ch); ch=getchar()) 25 num = (num<<1)+(num<<3)+ch-48; 26 return num*fl; 27 } 28 void addedge() 29 { 30 int u = read(), v = read(); 31 ll c = read(); 32 edges[++edgeTot] = Edge(v, c), nxt[edgeTot] = head[u], head[u] = edgeTot; 33 edges[++edgeTot] = Edge(u, c), nxt[edgeTot] = head[v], head[v] = edgeTot; 34 } 35 void insert(ll num) 36 { 37 used |= num; 38 for (int i=60, chk=0; i>=0&&!chk; i--) 39 if (num>>i){ 40 if (!p[i]) p[i] = num, chk = 1, ++legal; 41 else num ^= p[i]; 42 } 43 } 44 void dfs(int x, int fa, ll c) 45 { 46 dis[x] = c, stk[++cnt] = x; 47 for (int i=head[x]; i!=-1; i=nxt[i]) 48 { 49 int v = edges[i].y; 50 if (v!=fa){ 51 if (dis[v]==-1) dfs(v, x, c^edges[i].val); 52 else insert(dis[v]^c^edges[i].val); 53 } 54 } 55 } 56 ll calc() 57 { 58 ll ret = 0, tmp = 0; 59 for (int i=60; i>=0; i--) 60 { 61 sum[0] = sum[1] = 0; 62 for (int j=1; j<=cnt; j++) 63 ++sum[(1ll*dis[stk[j]]>>i)&1]; 64 if ((used>>i)&1){ 65 tmp = (1ll*sum[0]*(sum[0]-1)/2ll+1ll*sum[1]*(sum[1]-1)/2ll)%MO; 66 tmp = (tmp+1ll*sum[0]*sum[1]%MO)%MO; 67 ret = (ret+1ll*tmp*pwr[legal-1]%MO*pwr[i])%MO; 68 }else{ 69 tmp = 1ll*sum[0]*sum[1]%MO; 70 ret = (ret+1ll*tmp*pwr[legal]%MO*pwr[i])%MO; 71 } 72 } 73 return ret; 74 } 75 int main() 76 { 77 memset(head, -1, sizeof head); 78 memset(dis, -1, sizeof dis); 79 n = read(), m = read(), pwr[0] = 1; 80 for (int i=1; i<=m; i++) addedge(); 81 for (int i=1; i<=60; i++) pwr[i] = pwr[i-1]*2ll%MO; 82 for (int i=1; i<=n; i++) 83 if (dis[i]==-1){ 84 memset(p, 0, sizeof p); 85 used = legal = cnt = 0; 86 dfs(i, i, 0); 87 ans = (ans+calc())%MO; 88 } 89 printf("%lld\n",ans); 90 return 0; 91 }
END



 浙公网安备 33010602011771号
浙公网安备 33010602011771号