堆与堆相关

堆(Heap)，是一颗完全二叉树（设树的高度为h，则h-1层全满，第h层连续缺失若干右叶子）。适合顺序存储。

堆中元素的父亲节点数组下标是本身的1/2(只取整数部分)，故堆的大部分操作复杂都都是log级别。

1. 大、小根堆及堆的维护
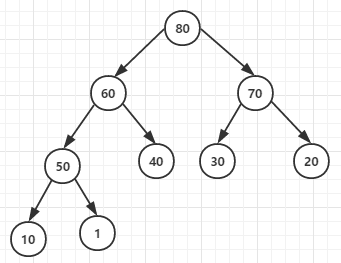
   如果每个数都大于等于自己的父结点，这个堆就叫做“大根堆”；
   
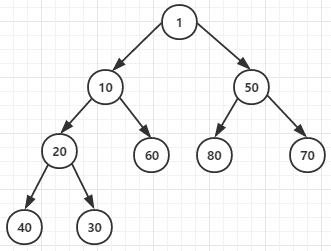
   相反，如果每个数都小于等于自己的父结点就叫做“小根堆”。
   
   小根堆的根节点的值是最小值，大根堆的根节点的值是最大值。
   注意：堆内的元素并不一定数组下标顺序来排序的！！很多的初学者会错误的认为大/小根堆中下标为1就是第一大/小，2是第二大/小……
   

   
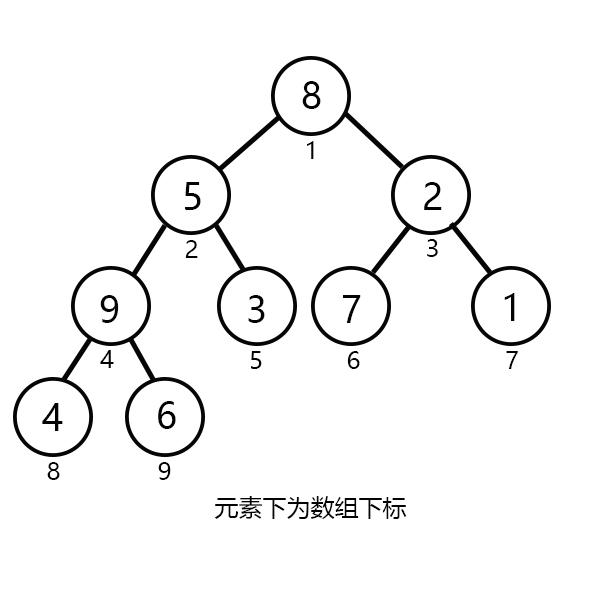
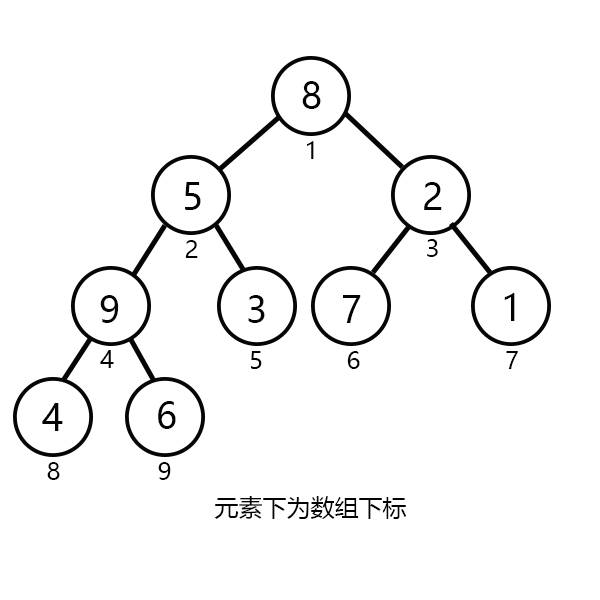
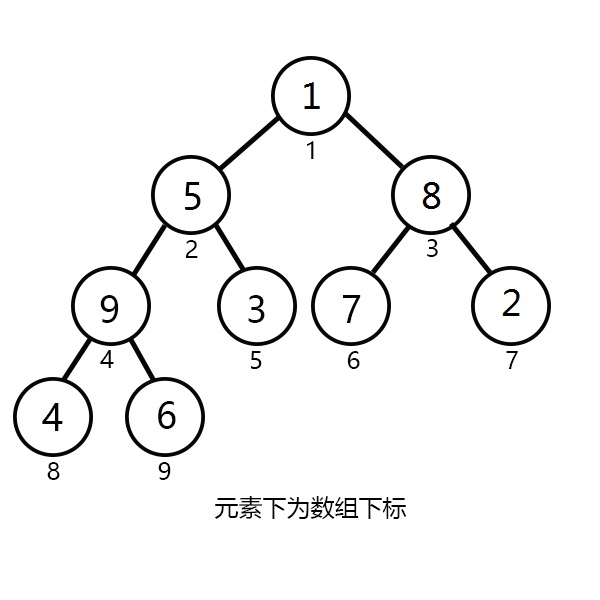
   实例：例如，我们要把 {8，5，2，10，3，7，1，4，6} 维护成一个小根堆。
   初状态如下：
   

   
   

   
   如何将这组杂乱无章的的数据维护成小根堆呢？堆有如下几个基本操作：
   

   • 上浮 shift_up；
   • 下沉 shift_down
   • 插入 push
   • 弹出 pop
   • 取顶 top
   • 堆排序 heap_sort

   显然，根节点1（元素8）不是最小的。我们很容易发现它的一个子节点3(元素2)比它更小，我们怎么将它放到最高点呢？直接交换就好。
   但是，我们又发现了，3的一个子节点7(元素1)似乎更适合在根节点。这下没法直接交换了，我们就要采用上浮操作了。
   上浮：把当前节点与其父亲节点比较：若比父亲节点小，交换这两个节点，并把当前询问的节点更新为原父亲节点（即继续向上询问）；否则退出。

   伪代码：

   1 Shift_up( i ){
   2     while( i / 2 >= 1)
   3     {
   4         if(Heap_a[ i ] < Heap_a[ i/2 ] ){
   5             swap( Heap_a[ i ] , Heap_a[ i/2 ]) ;
   6             i = i / 2;
   7         }
   8         else break;
   9 ｝

   子节点7(元素1)上浮后，堆状态如下：
   

   我们又发现了一个问题：节点3(元素8)的位置不太对劲，而它的子节点7(元素2)才应该在那个位置。
   因此，我们将采用第二种操作：下沉。
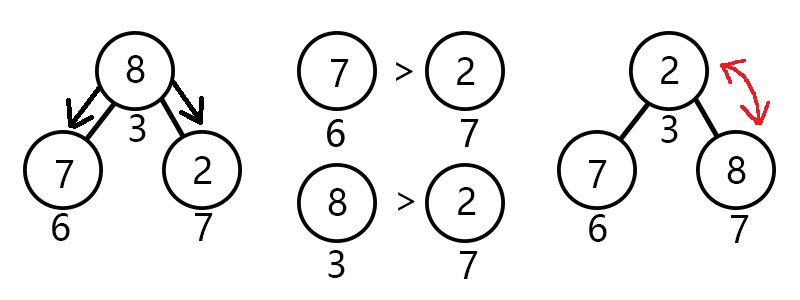
   那么问题来了：节点3(元素8)应该往哪里下沉呢？
   我们知道，小根堆是尽力要让小的元素在较上方的节点，而下沉与上浮一样要以交换来不断操作，所以应该让节点7(元素2)与之交换。
   由此我们可知，下沉：让当前结点的左右儿子(如果有的话)作比较，哪个比较小就和它交换，并更新询问节点的下标为被交换的儿子节点下标（即继续向下询问），否则退出。
   

   伪代码：

   Shift_down( i , n ) {   //n表示当前有n个节点
       while( i * 2 <= n) {
           T = i * 2 ;
           if( T + 1 <= n && Heap_a[ T + 1 ] < Heap_a[ T ])
               T++;
           if( Heap_a[ i ] < Heap_a[ T ] ){
              swap( Heap_a[ i ] , Heap_a[ T ] );
               i = T;
           }
           else break;
   }

   接下来的一个肥肠重要的操作就是插入了，如何在插入元素的同时维护堆（以免堆变得杂乱无章）呢？
   其实只需要在最后（叶子层的空位的最左边）插入，然后使它上浮即可～
   伪代码：

   Push ( x ) {
           ++n;
           Heap_a[ n ] = x;
           Shift_up( n );
   }

   既然有了插入，相应的操作自然就是弹出啦，顾名思义，弹出即把堆顶元素弹飞（就像飞行员紧急逃生座椅～）。然而，一个显然的问题是——把堆顶元素弹飞岂不是会让堆断成两截、群龙无首？
   为了解决这个问题，一个机智的解决方案就是把堆顶元素与堆底元素交换，弹出新堆底元素（即原来的堆顶），然后把新堆顶下沉即可。（需要注意的是要判断堆是否为空）
   伪代码：

   Pop ( x ) {
           swap( Heap_a[1] , Heap_a[ n ] );
           n--;
           Shift_down( 1 );
   }

    然后就是取顶（取根节点）了，显然只要返回Heap_a[1]即可。同样，需要注意判断堆内是否有元素。

2. 堆排序
   堆排序实质是选择排序的改进版，可以把每一趟元素比较结果保存下来，以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。
   步骤：
   (1)将长度为n的待排序的数组维护成一个大根堆（小根堆）
   (2)将根节点与尾节点交换并输出此时的尾节点
   (3)重新维护剩余的n -1个节点
   (4)重复步骤2，步骤3直至构造成一个有序序列
   
   伪代码：

   Heap_sort( ans[] ){
           k=0;
           while( Heap_a.size > 0 ) {
               k++;
               ans[ k ] = top();
               pop();    
           }        
   }

   复杂度为O(nlogn)，是不稳定排序。
   为什么是O(nlogn)呢？根据堆排序的过程，每次将大根堆根节点的值跟最后一个叶子的值进行交换，那如果最后的叶子结点正好是最小的数（最差情况），那么这个数就会一层层的最终放到叶子结点的位置，这样的话这个叶子结点经过的层数就刚好为log2(n)。

3. 优先队列
   优先队列是一种功能强大的队列。为什么说它功能强大呢？因为它可以做到自动排序～其实它的原理就是维护上文所述的二叉堆。所以重点在于:如何实现优先队列？
   所幸，C++有着一个强大的库：STL。STL里就有着优先队列，所以就不用手动实现了～
   
   首先，你需要这个头文件：

   #include<queue>

    声明一个优先队列的基本格式是：priority_queue<结构类型> 队列名; 
   例如：

   priority_queue <int> q;
   
   priority_queue <node> q;
   //node是一个结构体
   //结构体里重载了‘<’小于符号
   
   priority_queue <int,vector<int>,greater<int> > q;//注意后面两个“>”不要写在一起，“>>”是右移运算符
   priority_queue <int,vector<int>,less<int> >q;

   
   那么，对于这个以上三种优先队列q，我们可以做些什么呢？STL提供了如下标准方法：

   q.size();//返回q里元素个数
   q.empty();//返回q是否为空，空则返回1，否则返回0
   q.push(k);//在q的末尾插入k
   q.pop();//删掉q的第一个元素
   q.top();//返回q的第一个元素
   q.back();//返回q的末尾元素

   这些方法是通用的，不过以上三种优先队列还是有许多性质的不同：
   
   (1)默认优先队列，默认类型
   
   

   典型代表：

   priority_queue <int> i;
   priority_queue <double> d;

   向队列i中依次插入如下值：10、8、12、14、6；

    q.push(10),q.push(8),q.push(12),q.push(14),q.push(6);
       while(!q.empty())
           printf("%d ",q.top()),q.pop();

   输出为14 12 10 8 6
这说明了默认优先队列默认类型是按从大到小排序的！
   
   (2)默认优先队列，结构体
   
   典型代表：

   priority_queue <node> q;
   //node是一个结构体
   //结构体里重载了‘<’小于符号

   首先来看一下这个node结构体是何方神圣：

   struct node{
       int x,y;
       bool operator < (const node & a) const{return x<a.x;}
   };

   这个node结构体有两个成员，x和y，它的小于规则是x小者小。

   向队列q中依次插入如下值：(10,100),(12,60),(14,40),(6,20),(8,20)；

   k.x=10,k.y=100; q.push(k);
   k.x=12,k.y=60; q.push(k);
   k.x=14,k.y=40; q.push(k);
   k.x=6,k.y=80; q.push(k);
   k.x=8,k.y=20; q.push(k);
   while(!q.empty()){
       node m=q.top(); q.pop();
       printf("(%d,%d) ",m.x,m.y);
   }

    

   输出为(14,40) (12,60) (10,100) (8,20) (6,80)，即它也是按照重载后的小于规则，从大到小排序的。
   
   (3)less和greater的优先队列
   
   典型代表（以int为例）：

   priority_queue <int,vector<int>,greater<int> > q;//注意后面两个“>”不要写在一起，“>>”是右移运算符
   priority_queue <int,vector<int>,less<int> >q;

   再次尝试(1)中的数据：

   priority_queue <int,vector<int>,less<int> > p;
   priority_queue <int,vector<int>,greater<int> > q;
   int a[5]={10,12,14,6,8};
   int main()
   {
       for(int i=0;i<5;i++)
           p.push(a[i]),q.push(a[i]);
   
       printf("less<int>:")
       while(!p.empty())
           printf("%d ",p.top()),p.pop();  
   
       pritntf("\ngreater<int>:")
       while(!q.empty())
           printf("%d ",q.top()),q.pop();
   }

    

   结果：
   less<int>:14 12 10 8 6 
   greater<int>:6 8 10 12 14
   由此可知，less是从大到小，greater是从小到大。
   
   总结：常用优先队列：

   priority_queue<int,vector<int>,less<int> >q;
   priority_queue<int,vector<int>,greater<int> >q;

    

   
   
   

优先队列题目：
　　POJ：3253、2431、3614