[复习] 暑期打板

高考完了，耍了快一个月，开始边耍边学习😂

一年多没碰OI了，本来想刷点题回忆下
然鹅老年人记忆力不允许😭先打板吧

高精加

#include<bits/stdc++.h>
using namespace std;

const int N=600;
char ch[N];
int a[N],b[N],n,m,c[N],x;

int main(){

    // freopen("1.in","r",stdin);

    cin>>ch;
    n=strlen(ch);
    for(int i=0;i<n;++i)
        a[n-i]=ch[i]-48;
    
    cin>>ch;
    m=strlen(ch);
    for(int i=0;i<m;++i)
        b[m-i]=ch[i]-48;
    
    if(n<m) n=m;

    x=0;
    for(int i=1;i<=n;++i){
        c[i]=(a[i]+b[i]+x)%10;
        x=(a[i]+b[i]+x)/10;
    }
    if(x>0) ++n, c[n]=x;
    for(int i=n;i>0;--i)
        printf("%d",c[i]);
    return 0;
}

高精乘

被坑了，注意判零（见32行）

#include<bits/stdc++.h>
using namespace std;

const int N=3000;
int na,nb,n,a[N],b[N],c[N];
char ch[N];

int main(){

    freopen("1.in","r",stdin);

    cin>>ch;
    na=strlen(ch);
    for(int i=0;i<na;++i)
        a[na-i-1]=ch[i]-48;
    
    cin>>ch;
    nb=strlen(ch);
    for(int i=0;i<nb;++i)
        b[nb-i-1]=ch[i]-48;
    
    for(int i=0;i<na;++i)
        for(int j=0;j<nb;++j)
            c[i+j]+=a[i]*b[j];
    
    for(int i=0;i<na+nb;++i){
        c[i+1]+=c[i]/10;
        c[i]%=10;
    }

    n=na+nb-1;
    while(c[n]==0 && n>0) --n;
    while(n>=0) printf("%d",c[n]),--n;
    
    // debug
    // printf("\n");
    // for(int i=0;i<na+nb;++i) printf("%d ",c[i]);

    return 0;
}

并查集

徒手写的时候没加merge
是不可以的：强制father[x]=y认亲可能会把x从原有的并查集里撕出来
多进行几个这种操作整张图就裂开了

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1;char ch=0;
    while(!isdigit(ch) && ch!='-') ch=getchar();
    if(ch=='-') ch=getchar(),f=-1;
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e4+5;
int n,m,father[N];

int getfather(int x){return father[x]==x?father[x]:father[x]=getfather(father[x]);}

void merge(int x,int y){
    x=getfather(x), y=getfather(y);
    if(x==y) return;
    father[x]=y;
    return;
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=n;++i) father[i]=i; //?
    while(m--){
        int z=in,x=in,y=in;
        if(z==1) merge(x,y);
        else{
            if(getfather(x)==getfather(y)) printf("Y\n");
            else printf("N\n");
        }
    }

    return 0;
}

转念一想不能强制father[x]=y认亲可以让他们的爸爸认亲啊
所以去掉merge函数，让原先merge(x,y)的地方变成father[getfather(x)]=getfather(y)
也是对的

二分答案

二分答案就是这样，对也对的离谱，错也错的离谱
明明思路没一点问题，结果还WA9个点
传送门

#include<bits/stdc++.h>
using namespace std;
#define in Read()
#define int long long

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e6+10;
int n,m,a[N],ans,l,r,mid;

signed main(){

    // freopen("1.in","r",stdin);

    n=in,m=in; l=1;
    for(int i=1;i<=n;++i) a[i]=in, r=max(r,a[i]);
    while(l<r){
        mid=(l+r+1)>>1;
        int sum=0;
        for(int i=1;i<=n;++i)
            if(a[i]>mid) sum+=a[i]-mid;
        if(sum>=m) l=(ans=mid);
        else r=mid-1;
        // printf("%d %d\n",l,r);
    }

    printf("%lld\n",ans);
    return 0;
    
}

顺带一提，分数规划也用二分法做，要推柿子
分数规划经典题是算性价比，\(n\)个物品性能\(a_i\)，价格\(b_i\)
最大化\(\frac{\sum a_i}{\sum b_i}\)
推柿子：

\[\frac{\sum a_i}{\sum b_i}> mid\\ \sum a_i -mid\sum b_i>0 \]

一个\(mid\)能使得上式成立则该\(mid\)合法

树状数组

复健，一打就会

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e6+10;
int n,m,t[N];

int lowbit(int i){return i&-i;}

void Add(int p,int x){
    while(p<=n){
        t[p]+=x;
        p+=lowbit(p);
    }
}

int Query(int p){
    int sum=0;
    while(p>0){
        sum+=t[p];
        p-=lowbit(p);
    }
    return sum;
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=n;++i) Add(i,in);
    for(int i=1;i<=m;++i){
        int opt=in, a=in, b=in;
        if(opt==1) Add(a,b);
        else printf("%d\n",Query(b)-Query(a-1));
    }

    return 0;
    
}

另外一题
区间加？看到区间第一反应是前缀和，想半天发现肯定不行啊
一看以前的记录，麻了是差分😂想反了

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e6+10;
int n,m,t[N],a[N];

int lowbit(int i){return i&-i;}

void Add(int p,int x){
    while(p<=n){
        t[p]+=x;
        p+=lowbit(p);
    }
}

int Query(int p){
    int sum=0;
    while(p>0){
        sum+=t[p];
        p-=lowbit(p);
    }
    return sum;
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=n;++i) Add(i,(a[i]=in)-a[i-1]);
    for(int i=1;i<=m;++i){
        int opt=in;
        if(opt==1){
            int l=in,r=in,x=in;
            Add(l,x), Add(r+1,-x);
        }else{
            int p=in;
            printf("%d\n",Query(p));
        }
    }

    return 0;
    
}

线段树

完蛋，数组大小要*4都搞忘了
证明如下：
\(n\)个数据，显然线段树层数为\(\lceil \log_2n\rceil\)，故所需空间：

\[\sum_{i=1}^{\lceil \log_2n\rceil}2^i=2\times 2^{\lceil \log_2n\rceil}-1\leq 2\times 2^{ \log_2n +1}-1 \leq 4n \]

#include<bits/stdc++.h>
using namespace std;
#define in Read()
#define int long long

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e5+5;
int n,m,tre[N<<2],a[N],laz[N<<2];

void push_up(int p){tre[p]=tre[p<<1]+tre[p<<1|1];}

void push_down(int l,int r,int p){
    if(!laz[p]) return;
    int mid=l+r>>1;
    laz[p<<1]+=laz[p];
    laz[p<<1|1]+=laz[p];
    tre[p<<1]+=laz[p]*(mid-l+1);
    tre[p<<1|1]+=laz[p]*(r-mid);
    laz[p]=0; return;
}

void build(int l,int r,int p){
    if(l==r) tre[p]=a[l];
    else{
        int mid=l+r>>1;
        build(l,mid,p<<1);
        build(mid+1,r,p<<1|1);
        push_up(p);
    } return;
}

void update(int L,int R,int val,int l,int r,int p){
    if(L<=l&&r<=R){
        tre[p]+=val*(r-l+1);
        laz[p]+=val;
    }else{
        push_down(l,r,p);
        int mid=l+r>>1;
        if(mid>=L) update(L,R,val,l,mid,p<<1);
        if(mid<R) update(L,R,val,mid+1,r,p<<1|1);
        push_up(p);
    } return;
}

int query(int L,int R,int l,int r,int p){
    if(L<=l&&r<=R) return tre[p];
    push_down(l,r,p);
    int mid=l+r>>1, res=0;
    if(mid>=L) res+=query(L,R,l,mid,p<<1);
    if(mid<R) res+=query(L,R,mid+1,r,p<<1|1);
    return res;
}

signed main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=n;++i) a[i]=in;
    build(1,n,1);
    for(int i=1;i<=m;++i){
        int opt=in;
        if(opt==1){
            int l=in,r=in,k=in;
            update(l,r,k,1,n,1);
        }else{
            int l=in,r=in;
            printf("%lld\n",query(l,r,1,n,1));
        }
    }

    return 0;
    
}

基础数学算法

分解质因子

虽然是\(O(N)\)算法，不够优秀（一般这些要分解的数比较大）
但是不常用，似乎没必要追求太优秀的方法

从i=2开始枚举每个数，能整除，则为质因子
每次务必除掉所有质因子

质数算法

判断质数

只需要\(2\)到\(\sqrt n\)所有数无法整除\(n\)就行了
\(O(N)\)

埃筛

\(O(N\times 较小倍数)\)（其实是\(O(N\log_2\log_2N)\)）
每次发现一个数\(i\)是质数，则筛掉\(i^2\)到\(n(i\cdot \lfloor\frac{n}{i}\rfloor)\)之间所有\(i\)的倍数
原因：\(i*1\)到\(i*i\)之间所有\(i\)的倍数已经在此前（处理\(<i\)的质数时）筛掉了

void get_prime(int n){
    memset(is_prime,true,sizeof(is_prime));
    is_prime[1]=false;
    for(int i=2;i<=n;++i){
        if(!is_prime[i]) continue;
        prime[++m]=i;
        int k=n/i;
        for(int j=i;j<=k;++j)
            is_prime[j*i]=false;
    }
}

线筛 | 欧拉筛

让每个合数只标记一次，复杂度降到\(O(n)\)
方法：遍历\(2\to n\)每个数时乘已筛出质数（到此，与埃筛一摸一样）
保证每个荷属只被标记一次的方法：让合数被其最小质因子标记
实现：if(!i%prime[j]) break

正确性证明：
对于\(i\bmod prime_j=0\)时，记\(k=i/prime_j\)
对于下一次筛掉\(i\times prime_{j+1}\)，变形得\(i\times prime_{j+1}=k\times prime_j\times prime_{j+1}\)
这个合数肯定会被更小一点的质数提前筛掉，那这一步（以及以后的步骤）都是没必要的
所以只需要在埃筛的基础上加一句if(!i%prime[j]) break就可以了

void get_prime(int n){
    memset(is_prime,true,sizeof(is_prime));
    is_prime[1]=false;
    for(int i=2;i<=n;++i){
        if(!is_prime[i]) continue;
        prime[++m]=i;
        for(int j=1;j<=m;++j){
            if(i*prime[j]>n) break;
            is_prime[i*prime[j]]=false;
            if(!i%prime[j]) break;
        }   
    }
}

求\(gcd\) - 辗转相除 | 欧几里得

特殊情况/边界条件：当\(b|a\)时，\(gcd(a,b)=b\)
当\(b\nmid a\)时，有\(gcd(a,b)=gcd(b,a\bmod b)\)，证明如下：
设\(a=bk+c\)，\(c=a\bmod b\)，设\(d|a,\ d|b\)，则\(c=a-bk,\ \frac{c}{d}=\frac{a}{d}-\frac{b}{d}k\)
显然\(\frac{c}{d}\)为整数，即\(d|c\)，若\(d\)取\(gcd(a,b)\)则得证

所以就有了这行极限压缩的代码

int gcd(int a,int b){return b?a:gcd(b,a%b);}

快速幂

把次数二进制化了，\(O(\log_2N)\)
计算\(a^b\)

int qpow(int a,int b){
    int ans=1;
    while(b){
        if(b&1) ans*=a;
        a*=a;
        b>>=1;
    }
    return ans;
}

线性求逆

\(ax\equiv1(\bmod\ b)\)则称\(x\)为\(a\)在模\(b\)下的逆元，记为\(a^{-1}\)

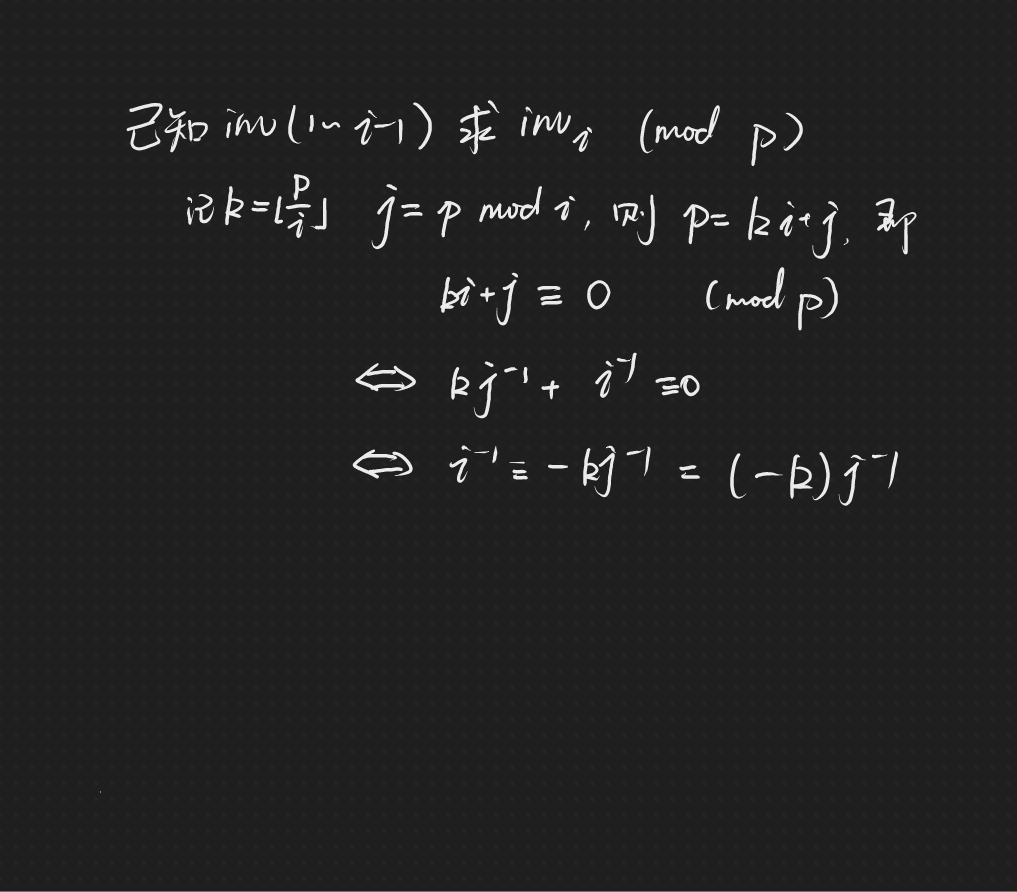
inv[i]=(mod-mod/i)*inv[mod%i]%mod
其他方法（扩欧、快速幂）咕了

主席树

先复习离散化

两个STL函数：
unique(start,end)：给一个有序序列去重（只是把重复部分放到末尾），并返回去重后的序列的最后一个元素的位置
lower_bound(start,end,x)：寻找第一个大于等于 x 的数，并返回这个数的位置

口诀：排序去重lower_bound

n=in;
for(int i=1;i<=n;++i) a[i]=b[i]=in;
// a[i]存放离散化结果
sort(b+1,b+n+1);
int cnt=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;++i) a[i]=lower_bound(b+1,b+n+1,a[i])-b;

待解决问题：unique函数为什么末尾要-1？

板题
桶排序+前缀和统计/询问

如果你懂了，细节上有点问题，那就享用如下的奶妈级标程吧！

#include<bits/stdc++.h>
#define in Read()
#define re register
inline int in{
	int i=0,f=1;char ch;
	while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
	if(ch=='-')f=-1,ch=getchar();
	while(ch<='9'&&ch>='0')i=(i<<1)+(i<<3)+ch-48,ch=getchar();
	return i*f;
}

const int NNN=2e5+10;
int n,m,size/*节点个数*/;
int a[NNN],b[NNN],Root[NNN]/*记录每个区间的根节点*/;
struct node{
	int lch,rch,sum;
}tree[NNN<<5];//主席树开32倍空间 

inline int build(int l,int r){
	int root=++size;
	if(l==r)return root;
	int mid=(l+r)>>1;
	tree[root].lch=build(l,mid);
	tree[root].rch=build(mid+1,r);
	return root;
}

inline int Update(int pre,int l,int r,int x){
	int root=++size;
	//新节点继承原节点的所有信息； 
	tree[root].lch=tree[pre].lch;
	tree[root].rch=tree[pre].rch;
	tree[root].sum=tree[pre].sum+1;
	
	if(l==r)return root;
	int mid=(l+r)>>1;
	if(x<=mid)tree[root].lch=Update(tree[pre].lch,l,mid,x);
	else tree[root].rch=Update(tree[pre].rch,mid+1,r,x);
	return root;
}

inline int Query(int u,int v/*目前相减两区间的根节点*/,int l,int r,int k){
	//l==r，搜到
	if(l==r)return l;
	
	//两个前缀和相减得到区间的左子树的权值大于k则第k大数在左边，反之在右边 
	int x=tree[tree[v].lch].sum-tree[tree[u].lch].sum,mid=(l+r)>>1;
	if(x>=k)return Query(tree[u].lch,tree[v].lch,l,mid,k);
	else return Query(tree[u].rch,tree[v].rch,mid+1,r,k-x);//细节：左边的权值都不算了 
}

int main(){
	n=in,m=in;
	
	//离散化 
	for(re int i=1;i<=n;++i)b[i]=a[i]=in;
	std::sort(b+1,b+n+1);
	int cnt=std::unique(b+1,b+n+1)-b-1;//这个东西是实际需要的叶子结点的个数 
	for(re int i=1;i<=n;++i)a[i]=std::lower_bound(b+1,b+cnt+1,a[i])-b;
	
	//建树与更新 
	Root[0]=build(1,cnt);
	for(re int i=1;i<=n;++i)Root[i]=Update(Root[i-1],1,cnt,a[i]);
	
	//查询
	for(re int i=1;i<=m;++i){
		int l=in,r=in,k=in;
		printf("%d\n",b[Query(Root[l-1],Root[r],1,cnt,k)]);//Query返回的是离散化之后的编号，要用b数组映射回去 
	}
	return 0;
}

图论相关

DFS
目标：每次尽量深
做标记：这个点走过没有
防止重走
递归实现

BFS
目标：（非人话）每次尽量宽（人话）每次遍历每层所有点
只要经过节点，节点就要做上标记，标记不能撤销
每个点都只会经过一次

愉快地进入最短路

Floyd
不用说了吧
三角形不等式（也叫松弛操作）

SPFA
就它可处理负边权问题：经过\(>n\)条边时一定存在负环
边界要卡准了，\(n-1\)条边都是可以的，\(n\)条边就不行了，边界给宽一点可能队列就已经清空了
容易卡成\(O(NM)\)，不建议使用

bool BFS(){
    memset(dis,0x7f,sizeof(dis));
    queue<int> q;
    q.push(st); vis[st]=true; dis[st]=0;
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int e=fst[u];e;e=nxt[e]){
            int v=aim[e];
            if(dis[v]>dis[u]+wei[e]){
                dis[v]=dis[u]+wei[e];
                cnt[v]=cnt[u]+1;
                if(cnt[v]>=n) return false;
                if(!vis[v]){
                    vis[v]=true;
                    q.push(v);
                }
            }
        }
    }
    return true;
}

伟大的Dijkstra
爱死你了

有一句优化不懂：if(vis[u]) continue; vis[u]=true;
为啥加了不会错？为啥不加就会T？
以前的笔记写的是：节点算过就不再算了
如果第一次算该节点之后再次遇到它可以找到更优的路径呢？

回答：不会错，是优秀的优化
由于用了优先堆，如果队列中有多个同样的点，那么最先拿出来的一定是距起点最近的
其他（相同）点肯定没有这个点最优，可以忽略

洛谷板题

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=5e5+10;
int n,st,m,tot,fst[N],nxt[N<<1],aim[N<<1],wei[N<<1],dis[N];
bool vis[N];
priority_queue<pair<int,int> >q;

void Add(int u,int v,int w){
    ++tot;
    nxt[tot]=fst[u];
    fst[u]=tot;
    aim[tot]=v;
    wei[tot]=w;
}

void Dijkstra(){
    // memset(dis,0x3f,sizeof(dis));
    dis[st]=0; q.push(make_pair(0,st));
    while(!q.empty()){
        int u=q.top().second; q.pop();
        if(vis[u]) continue; vis[u]=true;
        for(int e=fst[u];e;e=nxt[e]){
            int v=aim[e];
            if(dis[v]>dis[u]+wei[e]){
                dis[v]=dis[u]+wei[e];
                q.push(make_pair(-dis[v],v));
            }
        }
    }
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in,st=in;
    for(int i=1;i<=m;++i){
        int u=in,v=in,w=in;
        Add(u,v,w);
    }

    for(int i=1;i<=n;++i) dis[i]=2147483647;
    Dijkstra();
    for(int i=1;i<=n;++i) printf("%d ",dis[i]);
    return 0;
    
}

差分约束

会了最短路，就会差分约束
有时候过不了是因为SPFA判负环的边界要求太严格了
好玄学

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e4+10;
int n,m,tot,fst[N],nxt[N],aim[N],wei[N],s,dis[N],cnt[N];
bool vis[N];

void Add(int u,int v,int w){
    ++tot;
    nxt[tot]=fst[u];
    fst[u]=tot;
    aim[tot]=v;
    wei[tot]=w;
    return;
}

bool SPFA(){
    memset(dis,0x7f,sizeof(dis));
    queue<int> q;
    dis[s]=0; vis[s]=true;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop(); vis[u]=false;
        ++cnt[u];
        if(cnt[u]>n) return false;
        for(int e=fst[u];e;e=nxt[e]){
            int v=aim[e];
            if(dis[v]>dis[u]+wei[e]){
                dis[v]=dis[u]+wei[e];
                if(!vis[v]){
                    vis[v]=true;
                    q.push(v);
                }
            }
        }
    }
    return true;
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=m;++i){
        int u=in,v=in,w=in;
        Add(v,u,w);
    }
    s=n+1;
    for(int i=1;i<=n;++i) Add(s,i,0);

    if(!SPFA()) puts("NO");
    else for(int i=1;i<=n;++i) printf("%d ",dis[i]);
    return 0;
    
}

拓排

用于DAG有向无环图，只是一种思想
BFS，入度为0的点加入队列

旅行计划

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=2e5+10;
int n,m,deg[N],f[N];
vector<int> G[N];
queue<int> q;

void topo(){
    for(int i=1;i<=n;++i) if(!deg[i]) q.push(i), f[i]=1;
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int v:G[u]){
            f[v]=max(f[v],f[u]+1);
            --deg[v];
            if(!deg[v]) q.push(v);
        }
    }
}

int main(){

    freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=m;++i){
        int u=in,v=in;
        G[u].push_back(v);
        ++deg[v];
    }

    topo();
    for(int i=1;i<=n;++i) printf("%d\n",f[i]);
    return 0;
    
}

可能是我编译器的问题。。。
for(auto e:G[u]){int v=G[u][e]; ...;}居然用不起

不是编译器的问题
是人的问题
for(auto v:G[u])是在G[u]中枚举其所有元素，而不是标号，根本不需要枚举e

tarjan

其实topo sort不常见到，当年第一次用到它是在tarjan题里需要的
而且topo sort本身只是一种思想（与BFS|DFS一样的）
那就顺便把tarjan复习咯

tarjan算法
解决问题：找到DAG中的环对其进行操作（比如把环缩成一个大点）
具体方法：看代码，oi-wiki讲的很清楚了

板题
tarjan+拓排
先缩成DAG，然后拓排（直观的说就是一次DFS一次BFS）
缩点操作没想出来，过去的程序给出的想法是直接重构（很简单很暴力的想法，学着点！）
所以第一次每条边要能够被遍历
过去的我还是太菜只能按别人所说第一次建图用邻接表
现在就不必了，两次都用vector也能写

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=1e4+5;
int n,m,wei[N],dfn[N],low[N],tim,w[N],f[N];
int scc[N],cnt,deg[N];
bool ins[N],vis[N];
stack<int> s;
queue<int> q;
vector<int> G[N],T[N];
// G for the original graph, T for the rebuilt graph and is supposed for topo sorting

void Tarjan(int u){
    dfn[u]=low[u]=++tim;
    s.push(u), ins[u]=true;
    
    for(auto v:G[u]){
        if(!dfn[v]){
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(ins[v]) low[u]=min(low[u],dfn[v]);
    }

    if(dfn[u]==low[u]){
        ++cnt;
        while(s.top()!=u){
            scc[s.top()]=cnt;
            ins[s.top()]=false;
            wei[cnt]+=w[s.top()];
            s.pop();
        }
        scc[s.top()]=cnt;
        ins[s.top()]=false;
        wei[cnt]+=w[s.top()];
        s.pop();
    }
}

void Rebuild(){
    for(int u=1;u<=n;++u){
        for(auto v:G[u]){
            if(scc[u]==scc[v]) continue;
            T[scc[u]].push_back(scc[v]);
            ++deg[scc[v]];
        }
    }
}

void Topo(){
    for(int i=1;i<=cnt;++i) if(!deg[i]) q.push(i), vis[i]=true, f[i]=wei[i];
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(auto v:T[u]){
            if(vis[v]) continue;
            f[v]=max(f[v],f[u]+wei[v]);
            --deg[v];
            if(!deg[v]) q.push(v), vis[v]=true;
        }
    }
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=n;++i) w[i]=in;
    for(int i=1;i<=m;++i){
        int u=in,v=in;
        G[u].push_back(v);
    }

    for(int i=1;i<=n;++i)
        if(!dfn[i]) Tarjan(i);
    Rebuild();
    Topo();

    int ans=0;
    for(int i=1;i<=cnt;++i) ans=max(ans,f[i]);
    printf("%d\n",ans);
    return 0;
}

嘿嘿嘿一遍过嘿嘿嘿

割点

用tarjan
如果u是割点，那么找得到一个儿子v使得\(low_v\geq dfn_u\)

由于是无向图，low的定义就有点小变化（在这方面我翻了裸谷博客，好像没人讲清楚）
有向图中u表示：在u的子树中能够回溯到的最早的已经在栈中的结点
但在无向图中：能回溯到的最小时间戳
\(low_v\geq dfn_u\)说明搜到了一棵子树，v不为根，u为根且有很多子树，显然u是割点

#include<bits/stdc++.h>
using namespace std;
#define in Read()
#define pb push_back

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=2e4+10;
int n,m,low[N],dfn[N],cnt,root,ans;
bool cut[N];
vector<int> G[N];

void tarjan(int u){
    low[u]=dfn[u]=++cnt;
    int son=0;
    for(auto v:G[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                ++son;
                if(son>1||u!=root) cut[u]=true;
            }
        }else low[u]=min(low[u],dfn[v]);
    }
}

int main(){

    // freopen("1.in","r",stdin);

    n=in,m=in;
    for(int i=1;i<=m;++i){
        int u=in,v=in;
        G[u].pb(v), G[v].pb(u);
    }

    for(int i=1;i<=n;++i)
        if(!dfn[i]) root=i, tarjan(i);
    
    for(int i=1;i<=n;++i) ans+=cut[i];
    printf("%d\n",ans);
    for(int i=1;i<=n;++i) if(cut[i]) printf("%d ",i);
    
}

树

树是特别的图
但因为树的性质特殊，其算法就有另外一套思路了

LCA最近公共祖先

倍增算法，二进制思想
34排特判：如果\(lca(u,v)=u\)，则不必进行下一步

#include<bits/stdc++.h>
using namespace std;
#define in Read()

int in{
    int i=0,f=1; char ch=0;
    while(!isdigit(ch)&&ch!='-') ch=getchar();
    if(ch=='-') f=-1, ch=getchar();
    while(isdigit(ch)) i=(i<<1)+(i<<3)+ch-48, ch=getchar();
    return i*f;
}

const int N=5e5+10;
int n,m,r,f[N][25],dep[N],lg;
vector<int> G[N];

void DFS(int u,int fa){
    dep[u]=dep[fa]+1;
    for(int i=0;i<=lg;++i)
        f[u][i+1]=f[f[u][i]][i];

    for(auto v:G[u]){
        if(v==fa) continue;
        f[v][0]=u;
        DFS(v,u);
    }
}

int LCA(int u,int v){
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=lg;i>=0;--i)
        if(dep[f[u][i]]>=dep[v]){
            u=f[u][i];
            if(u==v) return u;
        }
    for(int i=lg;i>=0;--i)
        if(f[u][i]!=f[v][i])
            u=f[u][i], v=f[v][i];
    return f[u][0];
}

int main(){

    freopen("1.in","r",stdin);

    n=in,m=in,r=in;
    lg=log(n)/log(2)+1;
    for(int i=1;i<=n-1;++i){
        int u=in,v=in;
        G[u].push_back(v);
        G[v].push_back(u);
        if(!u || !v){
            puts("false");
            return 0;
        }
    }

    DFS(r,0);
    
    for(int i=1;i<=m;++i){
        int u=in,v=in;
        printf("%d\n",LCA(u,v));
    }
    return 0;
}

不知为何WA一个点

树剖

也叫轻重链剖分
重儿子：该节点所有子节点中子树最大的子节点（之一）
其他子节点叫轻儿子
重儿子组成的链叫重链
轻重链不会转换（记得虚实链是会转化的）

初始化：两次DFS
pre_DFS=> siz, faz, son, dep
DFS=> top, dfn
此后还要建树（线段树）