人工智能预习 ： 7.2 马尔可夫决策过程

马尔可夫决策过程

太抽象了，这玩意还是拿着例子做做。

马尔可夫决策过程（Markov Decision Process，MDP）严格的描述了强化学习所面临的环境。

在 MDP 中，环境是完全可观测的：当前状态能够完整刻画系统的运行过程。

几乎所有强化学习问题都可以被表示为 MDP：

• 最优控制问题，可以看作处理连续状态和行动的 MDP 问题。

• 部分可观察（Partially Observable）问题，可以转换为面向信念状态（Belief State）的MDP 问题。

• 赌博机（Bandit）问题，可以看作只有一个状态的 MDP 问题。

• 多智能体随机博弈（Stochastic Game）问题，可以近似为智能体与自然博弈的 MDP 问题。

马尔可夫过程 (Markov Process)

随机过程 （Stochastic Process）

随机过程 （Stochastic Process） ：随时间演化的一连串随机事件，每个时间点都对应一个可能出现多种取值的随机变量。

概率论的研究对象是静态的随机现象，而随机过程的研究对象是随时间演变的随机现象。

• 例如，天气随时间的变化、城市交通随时间的变化

在随机过程中，随机现象在某时刻 \(t\) 的取值是一个随机变量，用 \(S_t\) 表示。

随机过程可以表示为：\(\{ S_t: t \in T \}\)

已知历史信息 \((S_1, ..., S_t)\) 时，下一个时刻状态为 \(S_{t+1}\) 的概率为

\[P(S_{t+1} | S_1, ..., S_t) \]

马尔可夫性质 （Markov Property）

马尔可夫性质 （Markov Property）：当且仅当任意时刻的状态只取决于上一时刻的状态

\[P(S_{t+1}|S_t) = P(S_{t+1}|S_1, ..., S_t) \]

• 当前状态是未来的充分统计量，即下一个状态只取决于当前状态，而不会受到过去状态的影响

• 马尔可夫性可以简化运算，只要当前状态可知，所有的历史信息都不再需要了，利用当前状态信息就可以决定未来

状态转移矩阵 (State Transition Matrix) \(\mathcal{P}\)

对一个马尔科夫状态 \(s\) 及其后继状态 \(s'\)，状态转移概率 (State Transition Probability) 定义为

\[P_{ss'} = P(S_{t+1} = s' | S_t = s) \]

\(\mathcal{P}\) 包含从所有状态 \(s\) 到其所有后继状态 \(s'\) 的转移概率

\[\mathcal{P} \; = \begin{bmatrix} \mathcal{P}_{11} & \dots & \mathcal{P}_{1n} \\ \vdots & & \\ \mathcal{P}_{n1} & \dots & \mathcal{P}_{nn} \end{bmatrix} \]

其中矩阵的每一行元素之和都等于 \(1\)。

马尔可夫过程

马尔可夫过程是具有马尔可夫性质的随机过程。

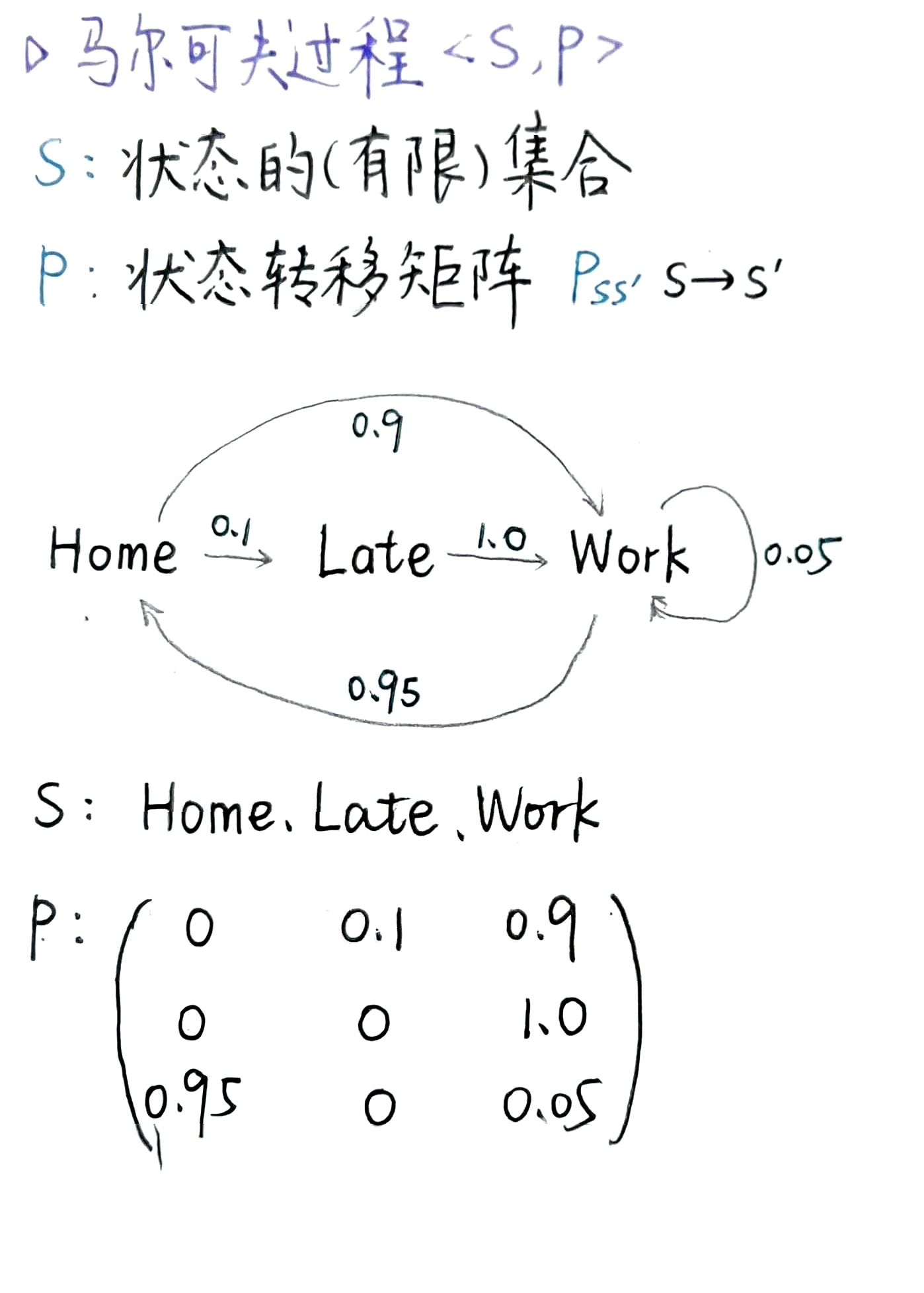
一个 马尔可夫过程 （Markov Process） 或 马尔可夫链 （Markov Chain） 可以表示为一个二元组 \(\langle \mathcal{S}, \mathcal{P} \rangle\)，其中：

• \(\mathcal{S}\) 是状态的（有限）集合。
• \(\mathcal{P}\) 是状态转移矩阵，\(P_{ss'} = P(S_{t+1} = s' \mid S_t = s)\)。

示例：通勤问题（详见 PPT ）

马尔可夫奖励过程 (Markov Reward Process)

马尔可夫奖励过程

一个马尔可夫奖励过程 （Markov Reward Process, MRP） 可以表示为一个四元组 \(\langle \mathcal{S}, \mathcal{P}, \mathcal{R}, \gamma \rangle\)，其中：

• \(\mathcal{S}\) 是状态的（有限）集合。
• \(\mathcal{P}\) 是状态转移矩阵，\(P_{ss'} = P(S_{t+1} = s' \mid S_t = s)\)
• \(\mathcal{R}\) 是奖励函数，\(R_s = \mathbb{E} [R_{t+1} \mid S_t = s]\)
• \(\gamma\) 是折扣因子，\(\gamma \in [0, 1]\)

在马尔可夫链基础上增加了“奖励”

折扣因子的引入 ： 远期收益具有一定的不确定性，有时我们更希望能够尽快获得一些奖励，所以对远期收益打一些折扣。

• 接近 \(1\) 的 \(\gamma\) 更关注长期的累计奖励，接近 \(0\) 的 \(\gamma\) 更考虑短期奖励

回报 （Return）

在一个马尔可夫奖励过程（MRP）中，在时间步 \(t\) 开始计算的 回报 （Return） \(G_t\) 指的是从时间步 \(t\) 开始累积的折扣奖励总和：

\[G_t = R_{t+1} + \gamma R_{t+2} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \]

其中，折扣因子 \(\gamma \in [0,1]\)，\(R_t\) 表示在时刻 \(t\) 获得的奖励。

价值函数 （State Value Function）

在一个马尔可夫奖励过程 （MRP） 中， 状态价值函数 （State Value Function） \(v(s)\) 定义为从状态 \(s\) 开始时的期望回报：

\[v(s) = \mathbb{E}[G_t \mid S_t = s] \]

价值函数 \(v(s)\) 表示状态 \(s\) 的长期价值，是从状态 \(s\) 开始的所有可能的马尔可夫链样本序列的回报 期望。

若从状态 \(s\) 开始的所有可能的马尔可夫链样本序列的集合为 \(\mathcal{T}\)，则

\[v(s) = \mathbb{E} [ G_t^\tau \mid \tau \in \mathcal{T} ] = \sum_{\tau \in \mathcal{T}} G_t^\tau \times P(\tau) \]

MRP 的贝尔曼方程（Bellman Equation）

价值函数可以分解为两部分：即时奖励 \(R_{t+1}\) + 后继状态折扣价值 \(\gamma v(S_{t+1})\)

\[\begin{align*} v(s) &= \mathbb{E}[G_t \mid S_t = s] \\ &= \mathbb{E}\left[ R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots \mid S_t = s \right] \\ &= \mathbb{E}\left[ R_{t+1} + \gamma \left( R_{t+2} + \gamma R_{t+3} + \dots \right) \mid S_t = s \right] \\ &= \mathbb{E}\left[ R_{t+1} + \gamma G_{t+1} \mid S_t = s \right] \\ &= \mathbb{E}\left[ R_{t+1} + \gamma v(S_{t+1}) \mid S_t = s \right] \end{align*} \]

\[v(s) = \mathcal{R}_s + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'} v(s') \]

其中，\(v(s)\) 是状态 \(s\) 的价值函数，\(\mathcal{R}_s\) 是状态 \(s\) 的即时奖励，\(\gamma\) 是折扣因子（用于权衡当前与未来奖励），\(\mathcal{P}_{ss'}\) 是从状态 \(s\) 转移到状态 \(s'\) 的概率，\(\mathcal{S}\) 是状态空间。

贝尔曼方程可简洁表示为矩阵形式：

\[\boldsymbol{v} = \mathcal{R} + \gamma \mathcal{P} \boldsymbol{v} \]

各符号含义：

• \(\boldsymbol{v}\)：列向量，每个元素对应一个状态的价值 \(v(s)\)，即 \(\boldsymbol{v} = \begin{bmatrix} v(S_1) \\ \vdots \\ v(S_n) \end{bmatrix}\) 。

• \(\mathcal{R}\)：奖励向量，\(\mathcal{R} = \begin{bmatrix} \mathcal{R}_{S_1} \\ \vdots \\ \mathcal{R}_{S_n} \end{bmatrix}\) ，元素为各状态的即时奖励。

• \(\mathcal{P}\)：状态转移概率矩阵，维度为 \(n \times n\)（\(n\) 为状态数 ），\(\mathcal{P} = \begin{bmatrix} \mathcal{P}_{S_1S_1} & \cdots & \mathcal{P}_{S_1S_n} \\ \vdots & \ddots & \vdots \\ \mathcal{P}_{S_nS_1} & \cdots & \mathcal{P}_{S_nS_n} \end{bmatrix}\) ，元素 \(\mathcal{P}_{ss'}\) 是状态转移概率。

\[\begin{bmatrix} v(S_1) \\ \vdots \\ v(S_n) \end{bmatrix} = \begin{bmatrix} \mathcal{R}_{S_1} \\ \vdots \\ \mathcal{R}_{S_n} \end{bmatrix} + \gamma \begin{bmatrix} \mathcal{P}_{S_1S_1} & \cdots & \mathcal{P}_{S_1S_n} \\ \vdots & \ddots & \vdots \\ \mathcal{P}_{S_nS_1} & \cdots & \mathcal{P}_{S_nS_n} \end{bmatrix} \begin{bmatrix} v(S_1) \\ \vdots \\ v(S_n) \end{bmatrix} \]

贝尔曼方程是线性方程组，可通过代数变形直接求解：

1. 从矩阵形式 \(\boldsymbol{v} = \mathcal{R} + \gamma \mathcal{P} \boldsymbol{v}\) 移项，得：

\[(\boldsymbol{I} - \gamma \mathcal{P}) \boldsymbol{v} = \mathcal{R} \]

其中 \(\boldsymbol{I}\) 是单位矩阵。

2. 两边同时左乘 \((\boldsymbol{I} - \gamma \mathcal{P})^{-1}\)（若矩阵可逆 ），解得：

\[\boldsymbol{v} = (\boldsymbol{I} - \gamma \mathcal{P})^{-1} \mathcal{R} \]

求解复杂度与适用场景

• 直接求解限制：当状态数为 \(n\) 时，求逆矩阵的计算复杂度为 \(O(n^3)\) ，因此仅适用于小规模马尔可夫奖励过程（MRP） 。

• 大规模场景方法：面对大规模 MRP，通常用迭代方法近似求解，常见方式有：

  • 动态规划（Dynamic Programming）
  • 蒙特卡洛评估（Monte-Carlo Evaluation）
  • 时序差分学习（Temporal-Difference Learning）

这些迭代方法通过逐步更新价值函数逼近最优解，避免了直接求逆的高复杂度，适配大规模状态空间场景。

马尔可夫决策过程(Markov Decision Process)

马尔可夫决策过程

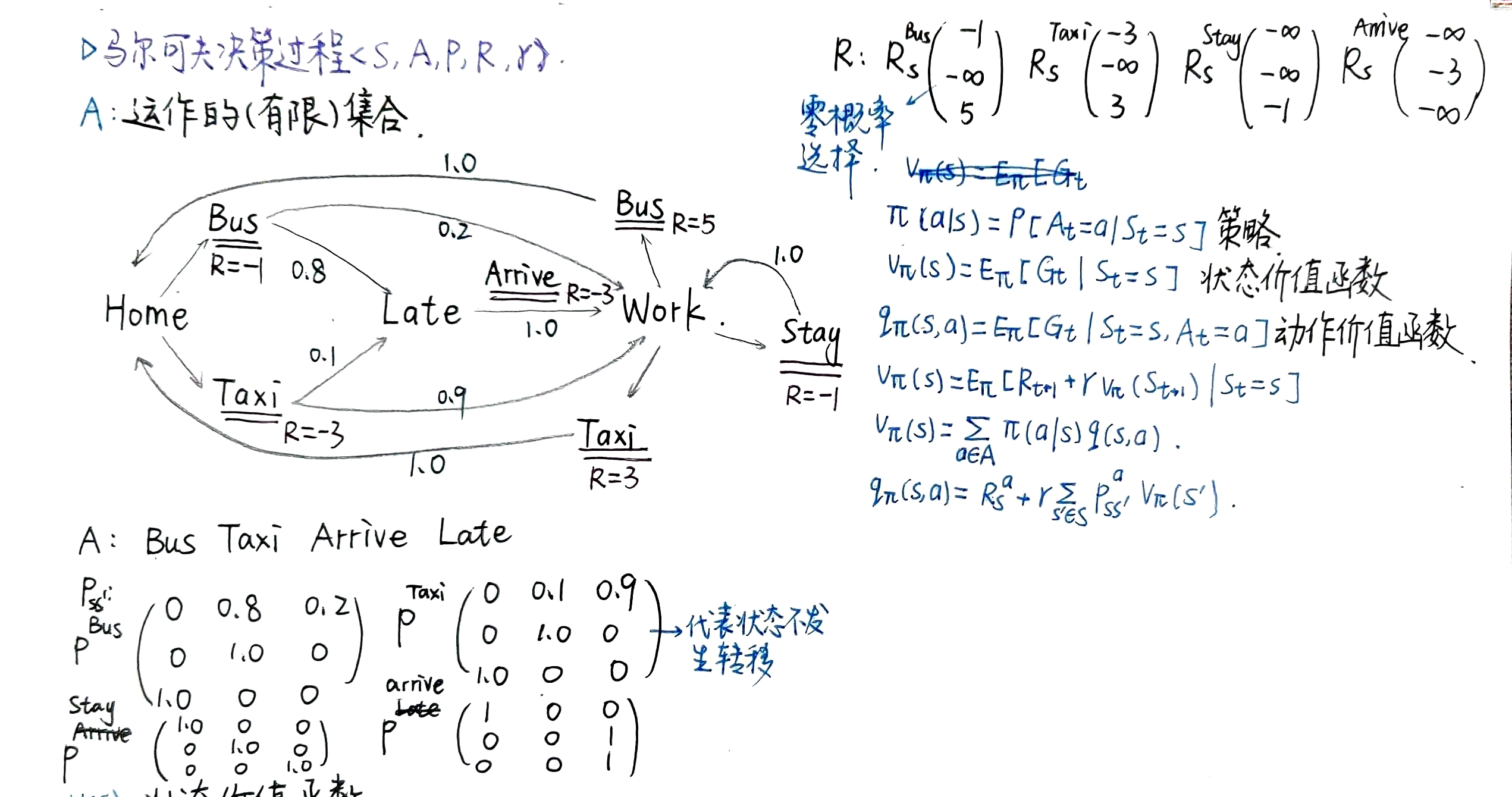
一个马尔可夫决策过程（Markov Decision Process, MDP） 可以表示为一个五元组 \(\langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma \rangle\)，其中：

• \(\mathcal{S}\) 是状态的（有限）集合
• \(\mathcal{A}\) 是动作的（有限）集合
• \(\mathcal{P}\) 是状态转移矩阵，\(\mathcal{P}_{ss'}^a = P(S_{t+1} = s' \mid S_t = s, A_t = a)\) ，描述在状态 \(s\) 执行动作 \(a\) 后转移到状态 \(s'\) 的概率
• \(\mathcal{R}\) 是奖励函数，\(\mathcal{R}_s^a = \mathbb{E}[R_{t+1} \mid S_t = s, A_t = a]\) ，表示在状态 \(s\) 执行动作 \(a\) 获得的期望即时奖励
• \(\gamma\) 是折扣因子，\(\gamma \in [0, 1]\) ，用于权衡当前奖励与未来奖励的重要性

马尔可夫决策过程是在马尔可夫奖励过程基础上增加了动作决策

策略

定义

策略（Policy） ： \(\pi\) 是在给定状态 \(s\) 时，采取各动作 \(a\) 的概率分布：

\[\pi(a \mid s) = P\left[A_t = a \mid S_t = s\right] \]

性质

• 决定智能体行为：策略完全决定了智能体在马尔可夫决策过程（MDP）中的行为。

• 马尔可夫性（与历史无关）：在 MDP 中，策略仅依赖于当前状态，与历史状态序列无关。

• 平稳性（与时间无关）：策略是平稳的，即不随时间步变化。对于任意 \(t > 0\)，动作 \(A_t\) 的分布满足：

  \[A_t \sim \pi(\cdot \mid S_t) \]

  这意味着策略仅由当前状态 \(S_t\) 决定，与具体时刻 \(t\) 无关。

价值函数

状态价值函数（State Value Function）

在给定策略 \(\pi\) 的 MDP 中，状态价值函数（State Value Function） \(v_\pi(s)\) 表示从状态 \(s\) 开始，随后按照策略 \(\pi\) 行动时的期望回报：

\[v_\pi(s) = E_\pi[G_t \mid S_t = s] \]

\[v_\pi(s) = E_\pi\left[ R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t = s \right] \]

\[v_\pi(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) q_\pi(s, a) \]

\[v_\pi(s) = \sum_{a \in \mathcal{A}} \pi(a \mid s) \left( \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v_\pi(s') \right) \]

动作价值函数（Action Value Function）

在给定策略 \(\pi\) 的 MDP 中，动作价值函数（Action Value Function） \(q_\pi(s, a)\) 表示从状态 \(s\) 开始，先执行动作 \(a\)，然后按照策略 \(\pi\) 行动时的期望回报：

\[q_\pi(s, a) = E_\pi[G_t \mid S_t = s, A_t = a] \]

\[q_\pi(s, a) = E_\pi\left[ R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) \mid S_t = s, A_t = a \right] \]

\[q_\pi(s, a) = \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v_\pi(s') \]

\[q_\pi(s, a) = \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a \sum_{a' \in \mathcal{A}} \pi(a' \mid s') q_\pi(s', a') \]

MDP 与 MP 和 MRP 的关系

给定一个马尔可夫决策过程（MDP）\(\mathcal{M} = \langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma \rangle\) 及策略 \(\pi\)，存在以下关系：

与马尔可夫过程（MP）的关系

状态序列 \(S_1, S_2, \dots\) 构成马尔可夫过程（Markov Process）：\(\langle \mathcal{S}, P^\pi \rangle\)

其中，\(P^\pi\) 是策略 \(\pi\) 下的状态转移概率，定义为：

\[P^\pi_{ss'} = \sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{P}^a_{ss'} \]

• \(\pi(a \mid s)\)：策略 \(\pi\) 在状态 \(s\) 下采取动作 \(a\) 的概率。
• \(\mathcal{P}^a_{ss'}\)：MDP 中状态 \(s\) 执行动作 \(a\) 后转移到 \(s'\) 的概率。

与马尔可夫奖励过程（MRP）的关系

状态-奖励序列 \(S_1, R_2, S_2, \dots\) 构成马尔可夫奖励过程（MRP）：\(\langle \mathcal{S}, \mathcal{P}^\pi, \mathcal{R}^\pi, \gamma \rangle\)

其中，\(\mathcal{R}^\pi\) 是策略 \(\pi\) 下的状态奖励，定义为：

\[\mathcal{R}^\pi_s = \sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{R}^a_s \]

• \(\mathcal{R}^a_s\)：MDP 中状态 \(s\) 执行动作 \(a\) 获得的即时奖励期望。

矩阵形式的贝尔曼期望方程

借鉴 MDP 与 MRP 之间的关系，贝尔曼期望方程可以使用矩阵形式简洁地表示为：

\[v_\pi = \mathcal{R}^\pi + \gamma \mathcal{P}^\pi v_\pi \]

直接结果为：

\[v_\pi = (I - \gamma \mathcal{P}^\pi)^{-1} \mathcal{R}^\pi \]

其中：

\[\mathcal{P}_{ss'}^\pi = \sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{P}_{ss'}^a \]

\[\mathcal{R}_s^\pi = \sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{R}_s^a \]

最优价值函数

最优状态价值函数（Optimal State Value Function）

\(v_*(s)\) 是对所有策略的状态价值函数的最大值：

\[v_*(s) = \max_\pi v_\pi(s) \]

最优动作价值函数（Optimal Action Value Function）

\(q_*(s, a)\) 是对所有策略的动作价值函数的最大值：

\[q_*(s, a) = \max_\pi q_\pi(s, a) \]

最优策略

在策略之间定义偏序关系：

\[\pi \geq \pi' \ \text{当且仅当} \ v_\pi(s) \geq v_{\pi'}(s), \ \text{对任意状态} \ s \]

对于任意马尔可夫决策过程（MDP）：

• 存在一个最优策略（Optimal Policy） ，它不劣于任何其他策略，即

\[\pi_* \geq \pi \ \text{对所有策略} \ \pi \ \text{都成立} \]

• 所有最优策略都能实现最优状态价值函数，即
  对所有状态 \(s\)，\(\displaystyle v_{\pi_*}(s) = v_*(s)\)

• 所有最优策略都能实现最优动作价值函数，即
  对所有状态 \(s\) 和动作 \(a\)，\(\displaystyle q_{\pi_*}(s, a) = q_*(s, a)\)

贝尔曼期望方程和贝尔曼最优方程

\(v_*\) 的贝尔曼最优方程（Bellman Optimality Equation）

\[v_*(s) = \max_a q_*(s, a) \]

\[v_*(s) = \max_{a} \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v_*(s') \]

\(q_*\) 的贝尔曼最优方程

\[q_*(s, a) = \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a v_*(s') \]

\[q_*(s, a) = \mathcal{R}_s^a + \gamma \sum_{s' \in \mathcal{S}} \mathcal{P}_{ss'}^a \max_{a'} q_*(s', a') \]

总结：

\[V_\pi(s) = \sum_{a \in A} \pi(a \mid s) \left( R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) V_\pi(s') \right), \]

\[V^*(s) = \max_{a \in A} \left( R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) V^*(s') \right), \]

\[Q_\pi(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) \sum_{a' \in A} \pi(a' \mid s') Q_\pi(s', a'), \]

\[Q^*(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) \max_{a' \in A} Q^*(s', a'). \]

部分可观察马尔可夫决策过程(Partially observable MDPs)

当状态不可完全观察时，通过引入观察和观察函数来扩展 MDP

一个部分可观察马尔可夫决策过程（Partially Observable Markov Decision Process, POMDP） 可以表示为一个七元组 \(\langle \mathcal{S}, \mathcal{A}, \mathcal{O}, \mathcal{P}, \mathcal{R}, \mathcal{Z}, \gamma \rangle\)，其中：

• \(\mathcal{S}\) 是状态的（有限）集合
• \(\mathcal{A}\) 是动作的（有限）集合
• \(\mathcal{O}\) 是观察的（有限）集合
• \(\mathcal{P}\) 是状态转移矩阵，\(\displaystyle P_{ss'}^a = P(S_{t+1} = s' \mid S_t = s, A_t = a)\)
• \(\mathcal{R}\) 是奖励函数，\(\displaystyle R_s^a = \mathbb{E}[R_{t+1} \mid S_t = s, A_t = a]\)
• \(\mathcal{Z}\) 是观察函数，\(\displaystyle Z_{s'o}^a = P(O_{t+1} = o \mid S_{t+1} = s', A_t = a)\)
• \(\gamma\) 是折扣因子，\(\gamma \in [0, 1]\)

历史（History）

历史（History） \(H_t\) 是动作、观测和奖励构成的序列：

\[H_t = A_0, O_1, R_1, \dots, A_{t-1}, O_t, R_t \]

信念状态（Belief State）

信念状态（Belief State） \(b(h)\) 是在给定历史 \(h\) 的条件下，对所有可能状态的概率分布：

\[b(h) = \big( P[S_t = s^1 \mid H_t = h], \dots, P[S_t = s^n \mid H_t = h] \big) \]