【A】1.4 单调栈/队列

单调栈

84.柱状图中最大的矩形

最大矩形的高度瓶颈可能在于各个柱子的高度，如图所示

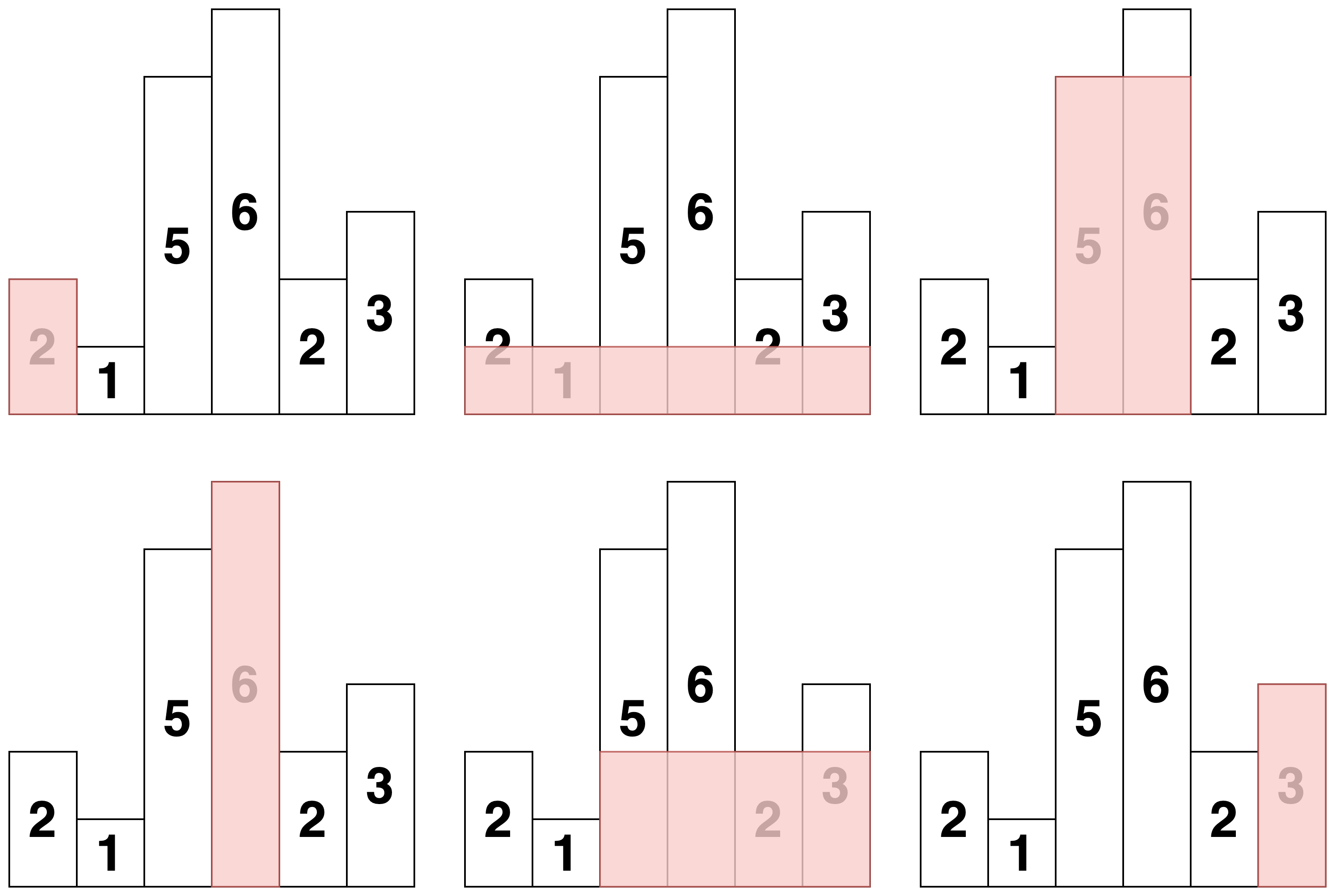
基于以上观察，一个朴素算法是：

1. 枚举每种可能的高度瓶颈
   1.1 向左、右扩展宽度
   1.2 擂台更新最大面积

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 记录绘制矩形的最大面积
        int boss = 0;
        // 枚举高度瓶颈
        for (int bn = 0; bn < heights.length; bn++) {
            // 探寻左右边界
            int lo = bn;
            int hi = bn;
            while (lo - 1 >= 0 && heights[lo - 1] >= heights[bn]) lo--;
            while (hi + 1 < heights.length && heights[hi + 1] >= heights[bn]) hi++;
            boss = Math.max(boss, (hi - lo + 1) * heights[bn]);
        }
        return boss;
    }
}

Smart mathematicians are not ashamed to think small. ———《具体数学》

为了加深对问题的理解，不妨从简单例子入手。不难发现：

• 若柱子高度单调递增，时间复杂度为\(O(n)\)
  • 从右至左累计宽度，当前面积 = 累计宽度 \(\times\) 当前高度
  • 擂台法更新最大矩形面积
• 若扫描至某处，单调性被破坏：
  • 不可扩展时，沿用历史记录即可，无需特别考虑
  • 可扩展时，情况可以等效于“柱子高度单调递增”

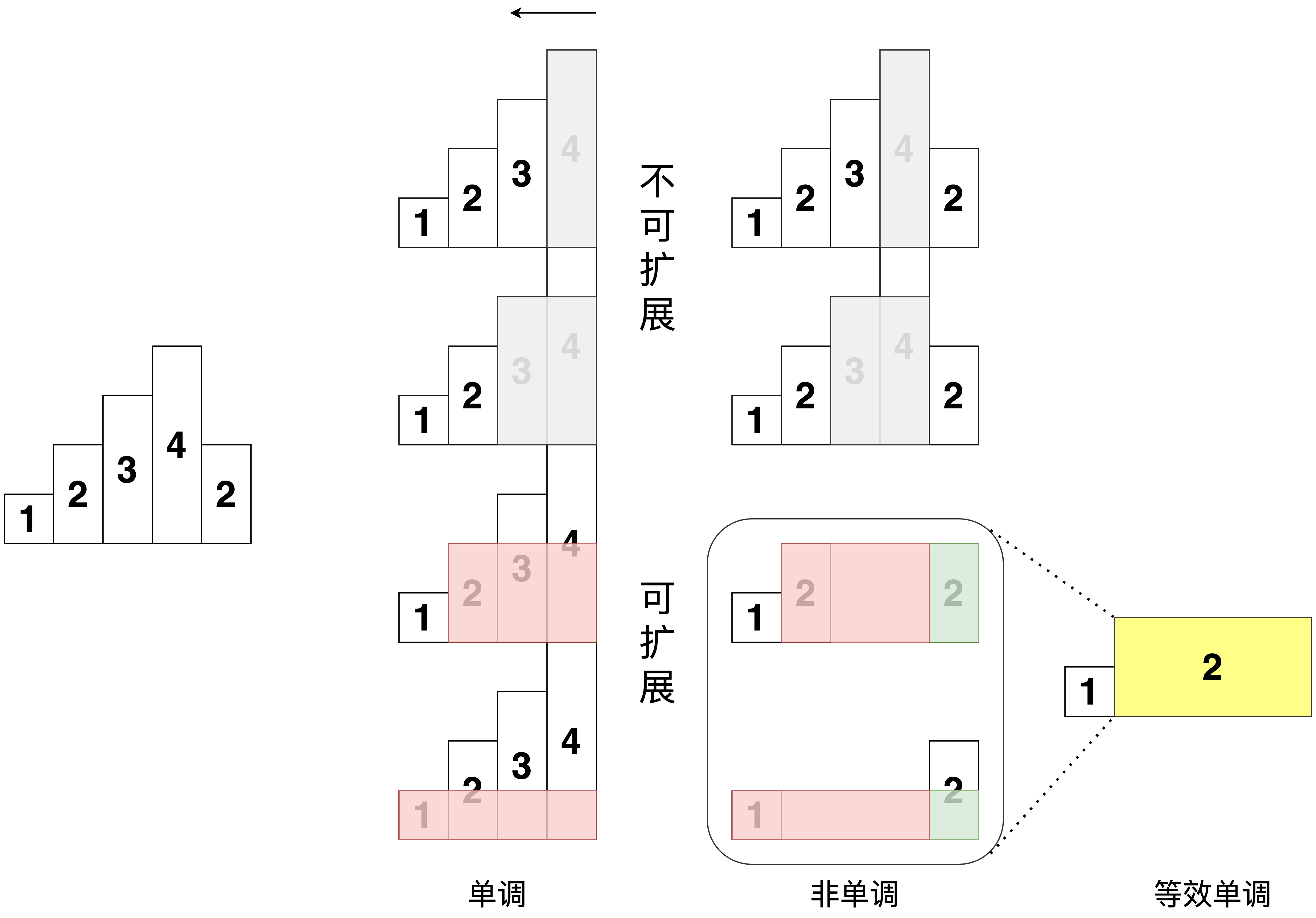
import java.util.ArrayDeque;
import java.util.Deque;

class Solution {
    public int largestRectangleArea(int[] heights) {
        Deque<Rect> s = new ArrayDeque<>();
        int ans = 0;
        for (int h : heights) {
            int width = 0;
            // 单调性破坏
            while (!s.isEmpty() && s.peek().h >= h) {
                width += s.peek().w;
                ans = Math.max(ans, width * s.peek().h);
                s.pop();
            }

            s.push(new Rect(width + 1, h));
        }

        int width = 0;
        while (!s.isEmpty()) {
            width += s.peek().w;
            ans = Math.max(ans, width * s.peek().h);
            s.pop();
        }

        return ans;
    }

    class Rect {
        int h;
        int w;

        Rect(int w, int h) {
            this.h = h;
            this.w = w;
        }
    }
}

85. 最大矩形

......

42. 接雨水

......

---

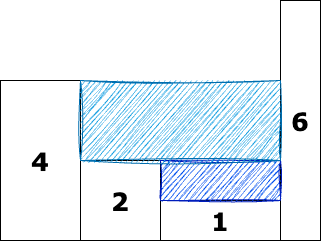
单调队列

单调队列是一种优化方法：以队列为容器维护一个候选集合，利用单调性排除永远不可能成为答案的选项，只保留某时刻可能成为答案的部分选项。

239. 滑动窗口最大值

可以考虑使用支持插入删除动态维护最大值的数据结构。本次我们先考虑单调队列的方法：

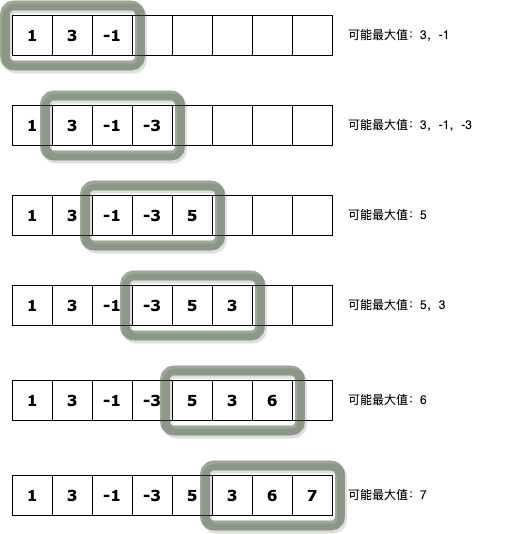
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        Deque<Integer> q=new ArrayDeque<>();
        int[] ans=new int[nums.length-k+1];
        int index=0;
        for(int i=0;i<nums.length;i++){
            // 出界
            while(!q.isEmpty()&&q.getFirst()<=i-k){
                q.pollFirst();
            }
            
            // 插入新选项，维护单调性
            while(!q.isEmpty()&&nums[q.getLast()] <= nums[i]){
                q.pollLast();
            }
            
            q.offerLast(i);
            
            // 取队头更新答案
            if(i>=k-1){
                ans[index++]=nums[q.peekFirst()];
            }
        }

        return ans;
    }
}