【A】1.1 数组

从逻辑结构而言，数组是一种线性表；从存储结构而言，一般认为，数组占用一组连续的内存空间，来存储一组具有相同类型的数据。因此，可以根据合法偏移量寻址，以随机访问数组元素。下面介绍保持相对顺序的数组过滤器相关习题（一般要求只使用常数的额外空间）。如同净水器滤除杂质，算法基本流程如下：

1. 顺序遍历数组元素
2. 检查是否符合条件
   2.1 符合条件 -> 留下
   2.2 不符合条件 -> 略过

遍历读取的过程，像是一个指针挥着衣袖，云彩依然在原地停留。“云彩”是（过滤前的）原始数据，虽然在访问过一次之后就没有利用价值了，但是它们依然无故地霸占着空间，白白地荒废着空间。所以，为何不把这些空间重新利用起来，新陈代谢、变废为宝呢？

要想达到这样高效的空间利用率，自然还需要另一个覆盖更新指针，它表示“当下一个符合条件的元素出现时，应当填写在哪个位置”，同时也作为计数器表示“当前已经维护好的，（过滤后的）新生数据的实际长度”。如果说读指针的前行，是稳扎稳打、快马加鞭，那么写指针的进展，就依靠条件而相对缓慢。

因此，它们也被形象地称为“快慢指针”。

---

👀那就自己动手试试叭
⚠️记得注意边界条件哦

刷题清单	过滤条件
27.移除元素	等于目标值就不要，不等于目标值就要
26.删除有序数组中的重复项	重复就不要，不重复就要（第一次出现）
283.移动零	为零就不要，不为零就要

这两题之所以不需要额外开辟临时数组，是因为其更新数据的覆盖进度总是比原始数据的访问进度要慢（更准确的说是，覆盖进度不领先于读取进度），进而不存在读取脏数据导致结果紊乱与原始数据遗失的问题。

88.合并两个有序数组

可是88这题，如果两个读指针、一个写指针照常置于数组头部，将比较小的一方填入，倘若不使用额外空间，就可能发生冲突。举例来说，此时此刻， \(nums_1\) 读指针指向的原始数据是3，如果直接更新于 \(nums_1\) 上，那么写指针就会领先读指针，把还没有访问的数据“吞”掉。

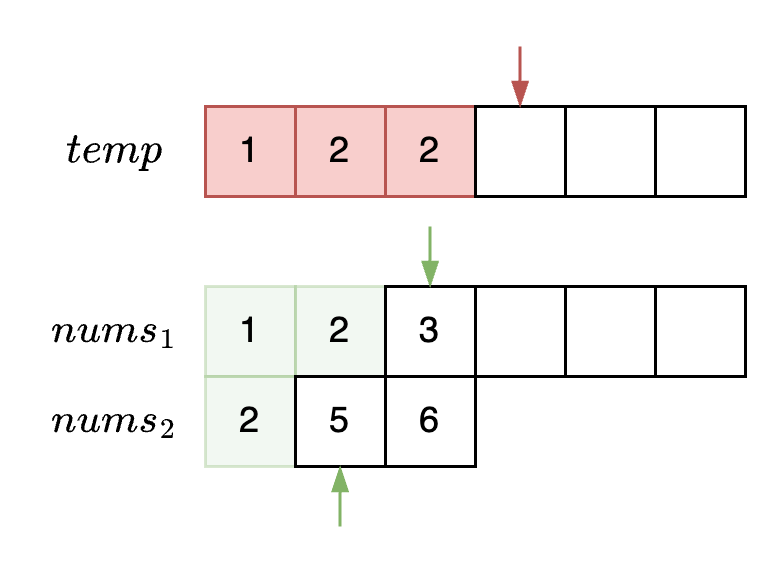
图1.1.1 😅

怎么办呢？观察发现， \(nums_1\) 后方有许多空位。
倘若读写指针均倒序更新，写指针将天然落后读指针。
我们可以想象，即使\(nums1\)的🐰读指针前期始终躺在原地，🐢写指针也追不上。于是，我们就可以直接在数组 \(nums_1\) 上原地修改，不需要额外空间！

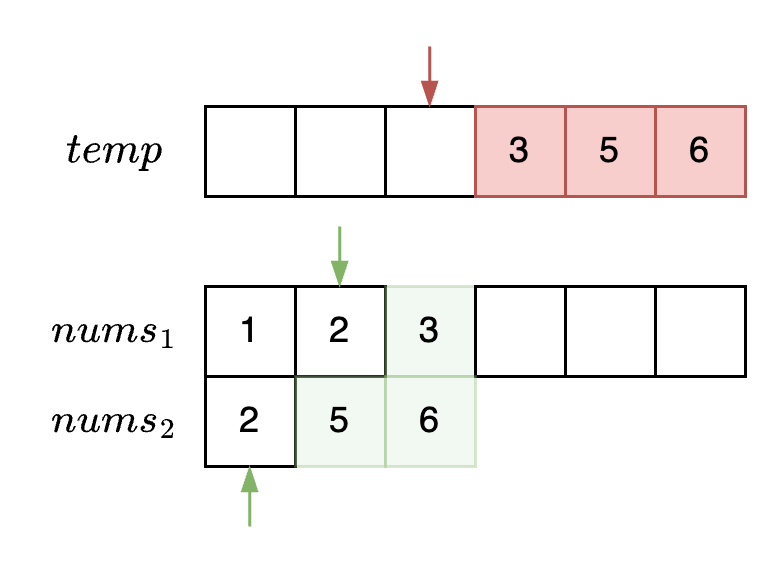
图1.1.2 😄

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        // 最新数据-写指针
        int w = nums1.length - 1;
        // 原始数据-读指针
        int r1 = m - 1;
        int r2 = n - 1;

        // 过滤条件：哪个更大填哪个
        while (r1 >= 0 && r2 >= 0)
            nums1[w--] = (nums1[r1] >= nums2[r2]) ? nums1[r1--] : nums2[r2--];

        // 某个数组触碰边界，另一个的元素直接挂载于尾部即可
        // while (r1 >= 0)
        //    nums1[w--] = nums1[r1--];
        while (r2 >= 0)
            nums1[w--] = nums2[r2--];
    }
}

977.有序数组的平方

对比来说，977与88题有相似也有不同。

• 相似在于，非理想情况下数组元素的绝对值符合“先递减后递增”的规律，仿佛就是两个序列拼接而成的。
• 不同在于，原地修改无法保证覆盖更新进度和读取访问进度不冲突，需要新开辟一个数组用于返回答案。

class Solution {
    public int[] sortedSquares(int[] nums) {
        // 用于返回答案
        int[] ans = new int[nums.length];

        // 原始数据-读指针
        int r1 = 0;
        int r2 = nums.length - 1;

        // 注意：倘若从读指针的角度切入，应当为 while(r1<=r2)
        for (int w = ans.length - 1; w >= 0; w--) {
            int s1 = nums[r1] * nums[r1];
            int s2 = nums[r2] * nums[r2];
            // 过滤条件：哪个绝对值更大填哪个的平方
            if (s1 >= s2) {
                ans[w--] = s1;
                r1++;
            } else {
                ans[w--] = s2;
                r2--;
            }
        }

        return ans;
    }
}