《算法图解》第六章 广度优先搜索

一、广度优先搜索(breadth-firsh search,BFS)
=>可回答问题:①从节点A出发,有前往节点B的路径吗?②从节点A出发,前往节点B的哪条路径最短?
=>最短路径问题(shorterst-path problem):简历模型,再使用广度优先搜索来解决。
二、图
(1)组成:节点(node)、边(edge)
(2)邻居:一个节点可能与总多的节点连接,这些节点被称为邻居。
(3)实现图:散列表的映射关系,由于散列表是无序的,键值对的添加顺序并不影响。
graph={} # “you”映射到一个数组,包括了“you”的所有邻居 graph["you"]=["alice","bob","claire"]
(4)类别:
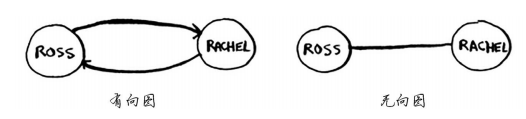
=>有向图(directed graph):边为箭头,箭头的方向指定了关系的方向。关系是单向的,被指向的节点是指向节点的邻居,注意当没有互相指向时,并不互为邻居的。
=>无向图(undirected graph):没有箭头,关系是双向的,直接相连的节点互为邻居。
(5) 实现算法:
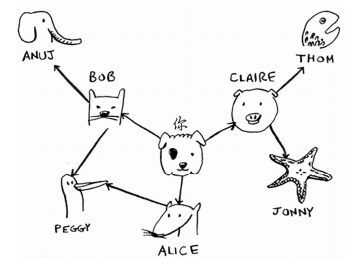
from collections import deque def person_is_seller(name): return name[-1]=='m' def search(name): # 创建一个队列 search_queue=deque() # 将邻居都加入这个搜索队列中 search_queue+=graph["you"] # 这个数组用于记录检查过的人 searched=[] while search_queue: person=search_queue.popleft() # 仅当这个人没检查时才检查 if not person in searched: if person_is_seller(person): print(person+" is a mango seller~!") else: search_queue+=graph[person] # 将这个人标记为检查过 searched.append(person) return False graph={} graph["you"]=["alice","bob","claire"] graph["bob"]=["anuj","peggy"] graph["alice"]=["peggy"] graph["claire"]=["thom","jonny"] graph["anuj"]=[] graph["peggy"]=[] graph["thom"]=[] graph["jonny"]=[] search("you")
*** 按加入顺序检查搜索列表中的人,否则找到的就不是最短路径,因此搜索列表必须是队列。
*** 对于检查过的人,务必不要再去检查,否则可能导致无限循环。
(6)运行时间:O(人数+边数)=O(V+E),其中V为顶点数,E为边数
(7)拓扑排序:A依赖于B,则A必须在B后,这是有序的。
三、队列(queue)
(1)【入队 / 压入 】和 【出队 / 弹出】:先进先出(First In Frist Out,FIFO)
(2)与栈的异同:不能随机地访问队列中的元素,栈是后进先出(Last In Frist Out,LIFO)。
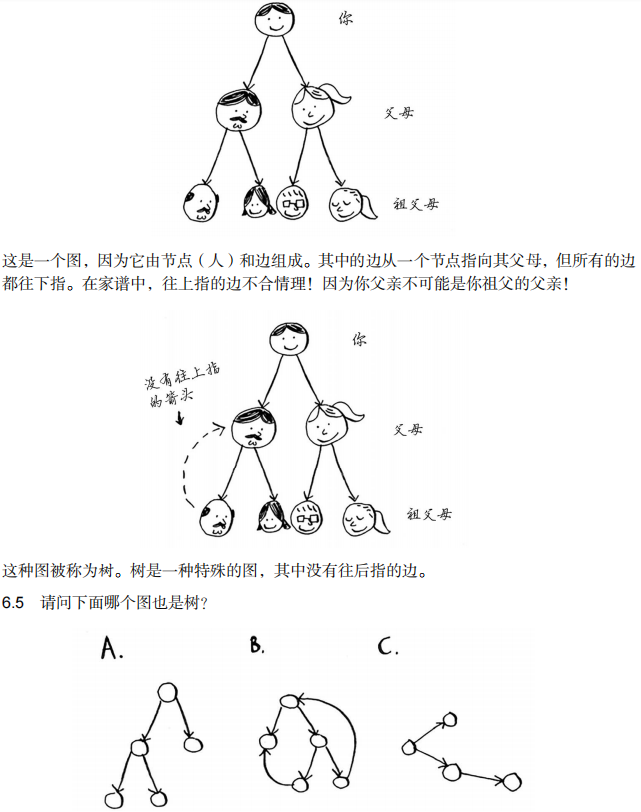
三、树(tree):所有的边都是向下指,没有往后指的边。
=>树是图的子集,树都是图,但是图不一定是树。
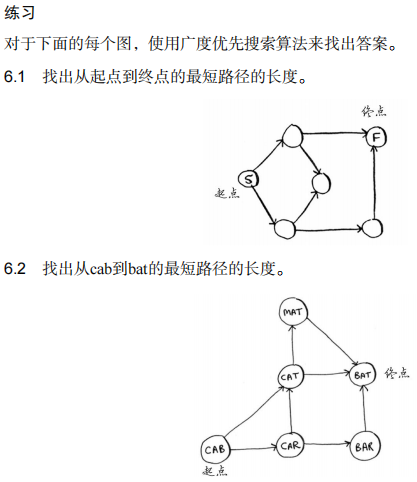
6.1 最短路径的长度为2
6.2 最短路径的长度为2
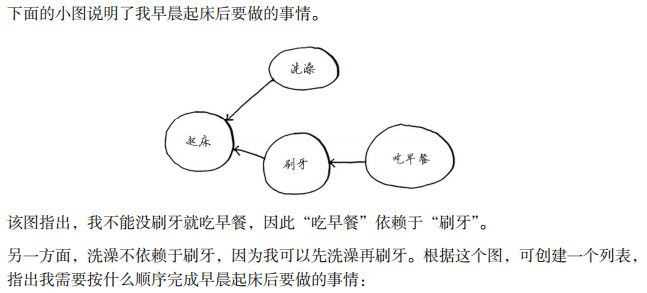
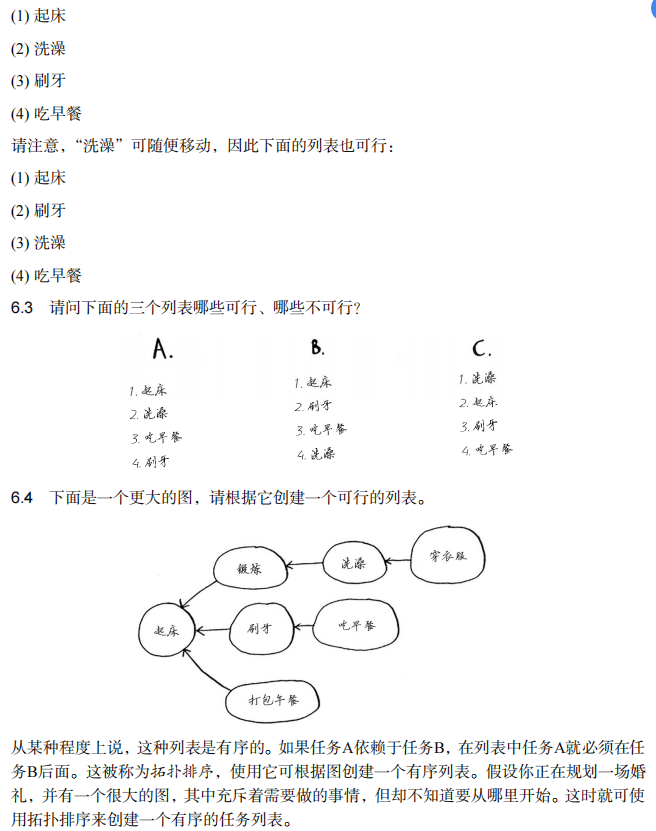
6.3 A不可行:吃早餐依赖于刷牙;B可行;C不可行:起床是起点。
6.4 1起床-2锻炼-3洗澡-4刷牙-5穿衣服-6打包午餐-7吃早餐
6.5 A是;B不是;C是。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号