《算法图解》第七章 狄克斯特拉算法

 

 一、加权图（weighted graph）

（1）提高或降低某些边的权重

（2）权重（weight）：每条边所关联的数字

　　 开销：从起点出发前往该节点所需要的时间。

（3）加权图（weighted graph）：带权重的图【计算加权图的最短路径，使用狄克斯特拉算法】

　　 非加权图（unweighted graph）：不带权重的图【计算最短路径，使用广度优先搜索】

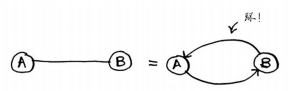
　　 环：无向图中两个节点彼此指向时，相当于环。

　　　　*** 在无向图中每条边都是一个环，狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。

　　　　

（4）负权边：贝尔曼-德福算法（Bellman-Ford algorithm）

 　　*** 不能将狄克斯特拉算法用于包含负权边的图。

（5）DEMO

 

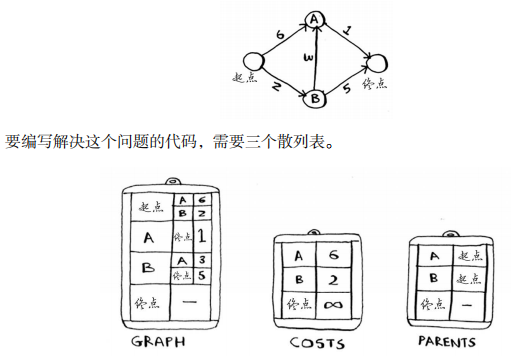
# 创建一个散列表

graph={}

# 将节点的所有邻居都存储在散列表中

graph["you"]=["alice","bob","claire"]

# 同时存储邻居和前往邻居的开销

graph["start"]={}

graph["start"]["a"]=6

graph["start"]["b"]=2

 

# ["a","b"]

print(graph["start"].keys())

 # 2

print(graph["start"]["b"])

 

# 添加其他节点及其邻居

graph["a"]={}

graph["a"]["fin"]=1

graph["b"]={}

graph["b"]["a"]=3

graph["b"]["fin"]=5

# 终点没有任何邻居

graph["fin"]={}

 

 # 开销列表

# 表示无穷

infinity=float("inf")

coats={}

coats["a"]=6

coats["b"]=2

coats['fin"]=infinity

 

# 存储父节点的散列表

parents={}

parents["a"]="start"

parents["b"]="start"

parents["fin"]=None

 

# 记录处理过的节点，保证对于同一个节点，不需要处理多次

processed=[]

 

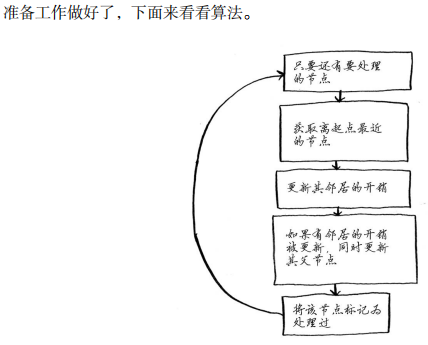
# 在未处理的节点中找出开销最小的节点

node=find_lower_cost_node(costs)

# while循环在所有节点都被处理后结束

while node is not None:

　　cost=costs[node]

　　# 遍历当前节点的所有邻居

　　for n in neighbors.keys():

　　　　new_cost=cost+neighbors[n]

　　　　# 如果经当前节点前往该邻居更近

　　　　if costs[n]<new_cost:

　　　　　　# 就更新该邻居的开销

　　　　　　costs[n]=new_cost

　　　　　　# 同时将该邻居的父节点设置未当前节点

　　　　　　parents[n]=node

　　# 将当前节点标记为处理过

　　processed.append(node)

　　# 找出接下来要处理的节点，并循环

　　node=find_lowest_cost_node(costs)

 

# 找出开销最低的节点

def find_lower_cost_node(costs):

　　lowest_cost=float("inf")

　　lowest_cost_node=None

　　# 遍历所有的节点

　　for node in costs:

　　　　cost=costs[node]

　　　　if cost<lowest_cost and node not in processed:

　　　　　　lowest_cost=cost

　　　　　　lowest_cost_node=node

　　return lowest_cost_node

 

 

 

 

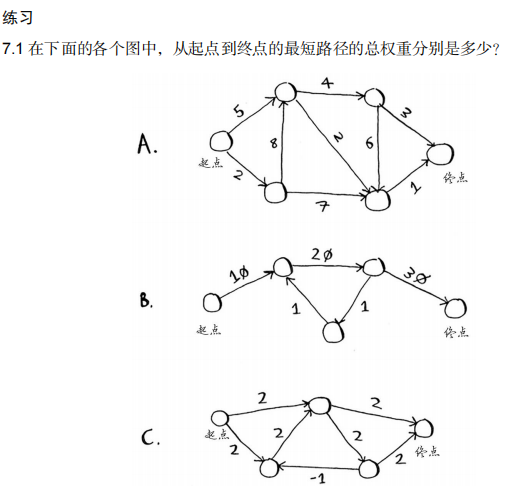
 7.1 A：5+2+1=8；B：10+20+30=60；C：2+2=4