PyTorch神经网络

神经元（Neuron）

神经元是神经网络的基本单元，它接收输入信号，通过加权求和后与偏置（bias）相加，然后通过激活函数处理以产生输出。

神经元的权重和偏置是网络学习过程中需要调整的参数。

输入和输出:

• 输入（Input）：输入是网络的起始点，可以是特征数据，如图像的像素值或文本的词向量。
• 输出（Output）：输出是网络的终点，表示模型的预测结果，如分类任务中的类别标签。

神经网络由多个层组成，包括：

• 输入层（Input Layer）：接收原始输入数据。
• 隐藏层（Hidden Layer）：对输入数据进行处理，可以有多个隐藏层。
• 输出层（Output Layer）：产生最终的输出结果。

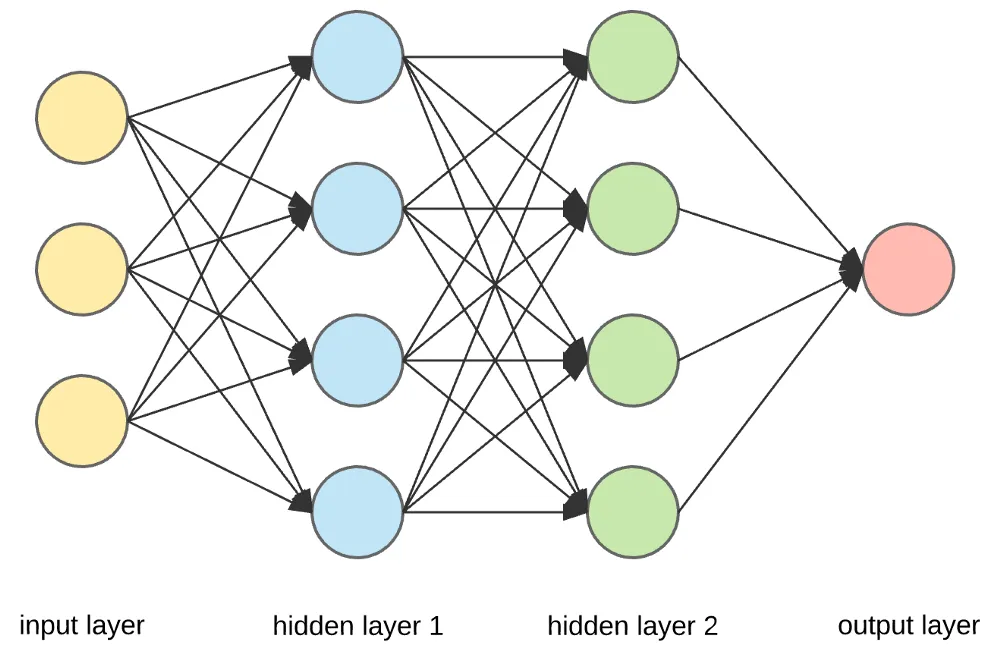
前馈神经网络（Feedforward Neural Network，FNN）

前馈神经网络特点是数据从输入层开始，经过一个或多个隐藏层，最后到达输出层，全过程没有循环或反馈。

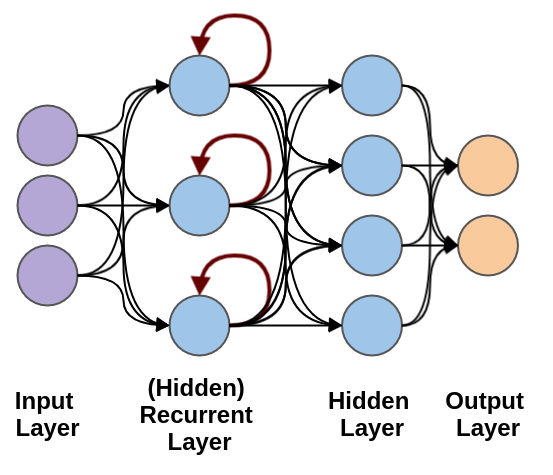
循环神经网络（Recurrent Neural Network, RNN）

循环神经网络（Recurrent Neural Network, RNN）络是一类专门处理序列数据的神经网络，能够捕获输入数据中时间或顺序信息的依赖关系。

循环神经网络用于处理随时间变化的数据模式。

 简单的全连接神经网络（Fully Connected Network）：

import torch
import torch.nn as nn

# 定义一个简单的神经网络模型
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        # 定义一个输入层到隐藏层的全连接层
        self.fc1 = nn.Linear(2, 2)  # 输入 2 个特征，输出 2 个特征
        # 定义一个隐藏层到输出层的全连接层
        self.fc2 = nn.Linear(2, 1)  # 输入 2 个特征，输出 1 个预测值
    
    def forward(self, x):
        # 前向传播过程
        x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数
        x = self.fc2(x)  # 输出层
        return x

# 创建模型实例
model = SimpleNN()

# 打印模型
print(model)

SimpleNN(
  (fc1): Linear(in_features=2, out_features=2, bias=True)
  (fc2): Linear(in_features=2, out_features=1, bias=True)
)

PyTorch 提供了许多常见的神经网络层，以下是几个常见的：

• nn.Linear(in_features, out_features)：全连接层，输入 in_features 个特征，输出 out_features 个特征。
• nn.Conv2d(in_channels, out_channels, kernel_size)：2D 卷积层，用于图像处理。
• nn.MaxPool2d(kernel_size)：2D 最大池化层，用于降维。
• nn.ReLU()：ReLU 激活函数，常用于隐藏层。
• nn.Softmax(dim)：Softmax 激活函数，通常用于输出层，适用于多类分类问题。

常见的激活函数包括：

• Sigmoid：用于二分类问题，输出值在 0 和 1 之间。
• Tanh：输出值在 -1 和 1 之间，常用于输出层之前。
• ReLU（Rectified Linear Unit）：目前最流行的激活函数之一，定义为 f(x) = max(0, x)，有助于解决梯度消失问题。
• Softmax：常用于多分类问题的输出层，将输出转换为概率分布。

损失函数用于衡量模型的预测值与真实值之间的差异。

常见的损失函数包括：

• 均方误差（MSELoss）：回归问题常用，计算输出与目标值的平方差。
• 交叉熵损失（CrossEntropyLoss）：分类问题常用，计算输出和真实标签之间的交叉熵。
• BCEWithLogitsLoss：二分类问题，结合了 Sigmoid 激活和二元交叉熵损失。

优化器（Optimizer）

优化器负责在训练过程中更新网络的权重和偏置。

常见的优化器包括：

• SGD（随机梯度下降）
• Adam（自适应矩估计）
• RMSprop（均方根传播）

训练过程（Training Process）

训练神经网络涉及以下步骤：

1. 准备数据：通过 DataLoader 加载数据。
2. 定义损失函数和优化器。
3. 前向传播：计算模型的输出。
4. 计算损失：与目标进行比较，得到损失值。
5. 反向传播：通过 loss.backward() 计算梯度。
6. 更新参数：通过 optimizer.step() 更新模型的参数。
7. 重复上述步骤，直到达到预定的训练轮数。

import torch
import torch.nn as nn
import torch.optim as optim  # 需导入优化器模块

# 1. 定义模型（关键缺失部分）
class SimpleLinearModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(SimpleLinearModel, self).__init__()
        self.linear = nn.Linear(input_dim, output_dim)  # 线性层：输入维度→输出维度
    
    def forward(self, x):
        return self.linear(x)  # 前向传播：直接通过线性层

# 2. 实例化模型（根据输入特征数和输出标签数定义）
# 这里X的特征数是2（每个样本2个特征），Y的输出维度是1，因此input_dim=2, output_dim=1
model = SimpleLinearModel(input_dim=2, output_dim=1)

# 3. 定义损失函数（关键缺失部分，这里用均方误差损失，适合回归任务）
criterion = nn.MSELoss()  # 均方误差损失，常用于回归问题

# 4. 定义优化器（关键缺失部分，这里用SGD优化器）
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 学习率lr=0.01

# 训练数据示例
X = torch.randn(10, 2)  # 10个样本，每个样本2个特征
Y = torch.randn(10, 1)  # 10个目标标签（回归任务，输出为连续值）

# 训练过程（逻辑不变，补充组件后可正常运行）
for epoch in range(100):  # 训练100轮
    model.train()  # 设置模型为训练模式
    optimizer.zero_grad()  # 清除上一轮的梯度
    output = model(X)  # 前向传播：输入X，得到预测输出
    loss = criterion(output, Y)  # 计算预测值与真实值的损失
    loss.backward()  # 反向传播：计算梯度
    optimizer.step()  # 更新模型参数
    
    if (epoch + 1) % 10 == 0:  # 每10轮输出一次损失
        print(f'Epoch [{epoch + 1}/100], Loss: {loss.item():.4f}')

Epoch [10/100], Loss: 0.9568
Epoch [20/100], Loss: 0.7692
Epoch [30/100], Loss: 0.6395
Epoch [40/100], Loss: 0.5494
Epoch [50/100], Loss: 0.4868
Epoch [60/100], Loss: 0.4430
Epoch [70/100], Loss: 0.4124
Epoch [80/100], Loss: 0.3909
Epoch [90/100], Loss: 0.3758
Epoch [100/100], Loss: 0.3651

神经网络类型

1. 前馈神经网络（Feedforward Neural Networks）：数据单向流动，从输入层到输出层，无反馈连接。
2. 卷积神经网络（Convolutional Neural Networks, CNNs）：适用于图像处理，使用卷积层提取空间特征。
3. 循环神经网络（Recurrent Neural Networks, RNNs）：适用于序列数据，如时间序列分析和自然语言处理，允许信息反馈循环。
4. 长短期记忆网络（Long Short-Term Memory, LSTM）：一种特殊的RNN，能够学习长期依赖关系。

 

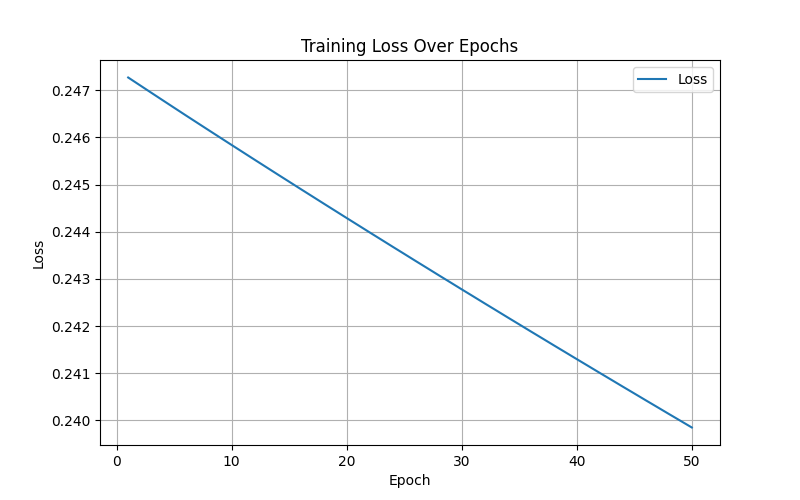
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

# 创建虚拟输入数据和目标数据
x = torch.randn(batch_size, n_in)  # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0], 
                  [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])  # 目标输出数据

# 创建顺序模型，包含线性层、ReLU激活函数和Sigmoid激活函数
model = nn.Sequential(
    nn.Linear(n_in, n_h),  # 输入层到隐藏层的线性变换
    nn.ReLU(),            # 隐藏层的ReLU激活函数
    nn.Linear(n_h, n_out),  # 隐藏层到输出层的线性变换
    nn.Sigmoid()           # 输出层的Sigmoid激活函数
)

# 定义均方误差损失函数和随机梯度下降优化器
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 学习率为0.01

# 用于存储每轮的损失值
losses = []

# 执行梯度下降算法进行模型训练
for epoch in range(50):  # 迭代50次
    y_pred = model(x)  # 前向传播，计算预测值
    loss = criterion(y_pred, y)  # 计算损失
    losses.append(loss.item())  # 记录损失值
    print(f'Epoch [{epoch+1}/50], Loss: {loss.item():.4f}')  # 打印损失值

    optimizer.zero_grad()  # 清零梯度
    loss.backward()  # 反向传播，计算梯度
    optimizer.step()  # 更新模型参数

# 可视化损失变化曲线
plt.figure(figsize=(8, 5))
plt.plot(range(1, 51), losses, label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Over Epochs')
plt.legend()
plt.grid()
plt.show()

# 可视化预测结果与实际目标值对比
y_pred_final = model(x).detach().numpy()  # 最终预测值
y_actual = y.numpy()  # 实际值

plt.figure(figsize=(8, 5))
plt.plot(range(1, batch_size + 1), y_actual, 'o-', label='Actual', color='blue')
plt.plot(range(1, batch_size + 1), y_pred_final, 'x--', label='Predicted', color='red')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.grid()
plt.show()