52+53线性回归

52线性回归（一）

women

plot(height,weight)

两者的线性关系：fit<-lm(weight~height,data=women)

 summary()展示拟合模型的详细结果：summary(fit)

线性回归（二）

对拟合线性模型有用的其他函数

abline(fit)绘制出拟合曲线

summary()展示拟合模型的详细结果

 coefficients(fit)列出拟合模型的模型参数（截距项和斜率）

 

 

 

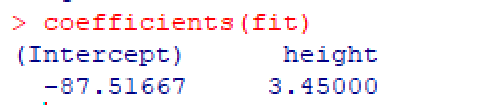
confint(fit)列出拟合模型的置信区间（默认95%）

 

 

 

fitted(fit)列出拟合模型的预测值

residuals(fit)列出拟合模型的残差值   残差=原数据-预测值

 

 

anova(fit)生成一个拟合模型的方差分析表

 

 

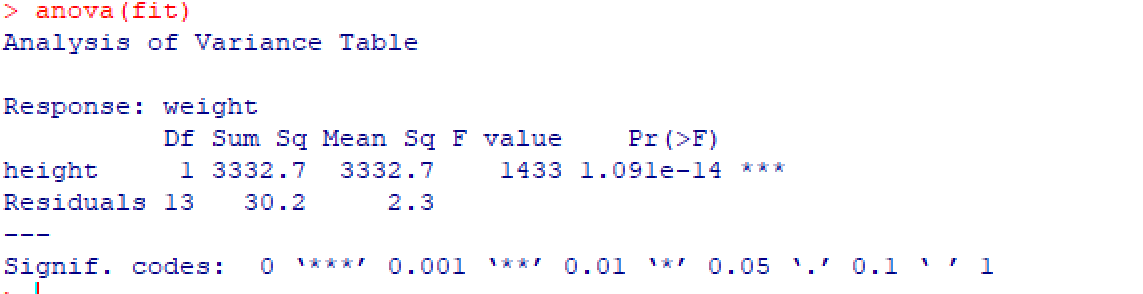
vcov(fit)列出模型参数的协方差矩阵

 

 

plot(fit)生成评价拟合模型的诊断图

predict(fit)用拟合模型对新的数据集预测响应变量值。

 

 

plot(women$height,women$weight)散点图

abline(fit)拟合线

线性回归：每个点到线的距离之和最小。

lm是用来适应线性模型的。它可用于进行回归、单层分析方差分析和协方差分析。

data:数据集data frame格式

state<-as.data.frame(state.x77[,c("Population","Murder","Illiteracy","Income","Frost")])

fit<-lm(Murder~Population+Illiteracy+Income+Frost,data=state)

1. 调用：Call

2.残差统计量：Residuals残差第一四分位数（1Q）和第三分位数（Q3）

3. 系数：Coefficients

intercept:截距

分别表示：估值,准误差,T值,P值

• Estimate的列：包含由普通最小二乘法计算出来的估计回归系数。
• Std. Error的列：估计的回归系数的标准误差。
• P值估计系数不显著的可能性，有较大P值的变量是可以从模型中移除的候选变量。
• t 统计量和P值：从理论上说，如果一个变量的系数是0，那么该变量是无意义的，它对模型毫无贡献。然而，这里显示的系数只是估计，它们不会正好为0。因此，我们不禁会问：从统计的角度而言，真正的系数为0的可能性有多大？这是t统计量和P值的目的，在汇总中被标记为t value和Pr(>|t|)。

 plot(fit)点是残差值，曲线是拟合曲线

1.横轴是y值（Fitted value），纵轴是残差（Residuals）

们希望看到残差的分布是比较均匀的，这样就代表误差分布符合Guaasian-Markov Condition。

2.Q-Q图（用来描述正态性），全程Quantile-Quantile图，是把两个分布的quantile放在一起进行比较

这幅图的作用就是检验误差是不是服从正态分布。如果是，这张图上的点将会贴近 这条直线。

3. Scale-Location

 位置和尺寸图，用来描述同方差性。满足不变方差，水平线旁边的点呈随机分布。

4. Residuals vs Leverage

残差与杠杆图

库克距离