CSP-S-2020
CSP-S-2020
T1 儒略日
向T1出题人致以最高的敬意(磕头)。
T2 动物园
简化题意:给出一些数,保证\(x∈[1,2^k-1]\)且互不相同,给出一些条件,如果存在数\(x\)第\(ai\)位为\(1\),那么就必须选物品\(bi\),\(bi\)互不相同。问有多少个数\(y\)满足不存在\(x=y\),并且加入\(y\)后选取的\(b\)不变。
很容易发现如果一个条件不被满足,即不存在数\(x\)第\(ai\)位为1,那么选取的数第\(ai\)位也必须为0。对于给出的\(k\)个位置,假设必须为0的位数有\(c\)个,那么剩下的数就有\(2^{k-c}\)个数加入后不会改变\(b\)的选取。再减去给出的\(n\)个数就得到了答案。
\(n=0,k=64\)的情况要特判,记得开\(unsigned\) \(long\) \(long\)。
#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long
const int N=1e6+5;
int n,m,c,k;
ll now,t[70];
int a[N];
int main()
{
scanf("%d %d %d %d",&n,&m,&c,&k);
t[0]=1;
for(int i=1;i<=k;++i) t[i]=t[i-1]*2;
now=0;ll x;
for(int i=1;i<=n;++i)
{
scanf("%llu",&x);
now|=x;
}
for(int i=1,b;i<=m;++i) scanf("%d %d",&a[i],&b);
sort(a+1,a+m+1);
a[0]=unique(a+1,a+m+1)-a-1;
int tmp=k;
for(int i=1;i<=a[0];++i)
{
if(a[i]>=tmp) break;
if((now&t[a[i]])==0) k--;
}
if(k==64&&n==0) printf("18446744073709551616");
else printf("%llu",(ll)t[k]-n);
return 0;
}
T3 函数调用
个人感觉这道题应该压轴啊,怎么会是T3。
30pts
线段树+递归的做法还是很好想到的,线段树只维护乘积,每次1操作的时候就先从线段树把乘积乘下去,再进行1操作,实现是\(O(logn)\),2操作直接在线段树根节点乘,实现是O(1)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5,M=1e6+5;
const ll mod=998244353;
int n,m,Q;
int tot,cz3[M];
struct node{int op,x,y;}cz[N];
ll val[N],mul[N<<2];
void Build(int l,int r,int p)
{
mul[p]=1;
if(l==r) return;
int mid=(l+r)>>1;
Build(l,mid,p<<1);
Build(mid+1,r,p<<1|1);
return;
}
void Spread(int p)
{
if(mul[p]==1) return;
int l=p<<1,r=p<<1|1;
mul[l]=mul[l]*mul[p]%mod;
mul[r]=mul[r]*mul[p]%mod;
mul[p]=1;
return;
}
void Change(int l,int r,int x,ll y,int p)
{
if(l==r)
{
val[l]=(val[l]*mul[p]+y)%mod;
mul[p]=1;
return;
}
Spread(p);
int mid=(l+r)>>1;
if(x<=mid) Change(l,mid,x,y,p<<1);
else Change(mid+1,r,x,y,p<<1|1);
return;
}
void Update(int l,int r,int p)
{
if(l==r)
{
val[l]=val[l]*mul[p]%mod;
return;
}
Spread(p);
int mid=(l+r)>>1;
Update(l,mid,p<<1);
Update(mid+1,r,p<<1|1);
return;
}
void Calc(int pos)
{
if(cz[pos].op==1) Change(1,n,cz[pos].x,(ll)cz[pos].y,1);
else if(cz[pos].op==2) mul[1]=mul[1]*cz[pos].x%mod;
else
{
for(int i=cz[pos].x;i<=cz[pos].y;++i)
Calc(cz3[i]);
}
return;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lld",&val[i]);
scanf("%d",&m);
for(int i=1;i<=m;++i)
{
scanf("%d",&cz[i].op);
if(cz[i].op==1) scanf("%d %d",&cz[i].x,&cz[i].y);
else if(cz[i].op==2) scanf("%d",&cz[i].x);
else
{
scanf("%d",&Q);
cz[i].x=tot+1;
for(int j=1;j<=Q;++j) scanf("%d",&cz3[tot+j]);
cz[i].y=(tot+=Q);
}
}
Build(1,n,1);
scanf("%d",&Q);
for(int i=1,x;i<=Q;++i)
{
scanf("%d",&x);
Calc(x);
}
Update(1,n,1);
for(int i=1;i<=n;++i) printf("%lld ",val[i]);
return 0;
}
100pts
线段树做法败在了3操作可以调用3操作,会进行很多重复计算,比如5调用2,8调用5(2,5,8为编号),最后给出的操作序列:2 5 8,那么操作顺序就是:2 5 2 8 5 2。重复调用将时间叠上去了。
满分思路是拓补排序,将每次操作都叠加在调用它的操作上,时间复杂度是\(O(n)\),不太好理解。
这种做法是将加法和乘法分开的。
举个例子:假设只有一个数\(2\),先进行\(*3\)操作,再\(+1\),再\(*2\),按照之前的思路,计算过程是\((2*3+1)*2\),加法乘法拆开后计算过程变成\(2*3*2+1*2\)。
因为每个乘法都是作用于整个数组的,对于一开始给出的数组,每个数扩大的倍数是一样的,所以把所有的操作跑一遍之后:\(ai=k*ai\)。
那么先讲乘法部分,即如何快速求出这个\(k\)。
乘法部分
首先要明白,最后给出的Q然后又进行一堆操作,可以看成一个3操作,即调用别的函数,假设编号为\(m+1\)。
于是把所有操作都向调用它的操作连边,就可以得到一张一定无环的有向图。(如果存在环,即\(a\)调用\(b\),\(b\)调用\(a\),会陷入死循环)
给出例图(为了方便理解,调用顺序假设都是从左到右调用):
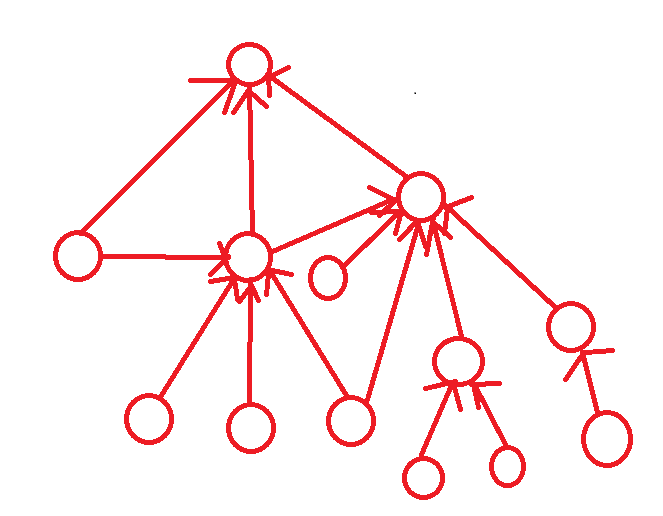
乘法的调用顺序并不影响最终值。
比如\(*3\)操作,如果后面蓝色框框里得到的乘积是\(*5\),那么现在整张图的乘积应该是\(*3*15\)。(对应黄路和紫路)
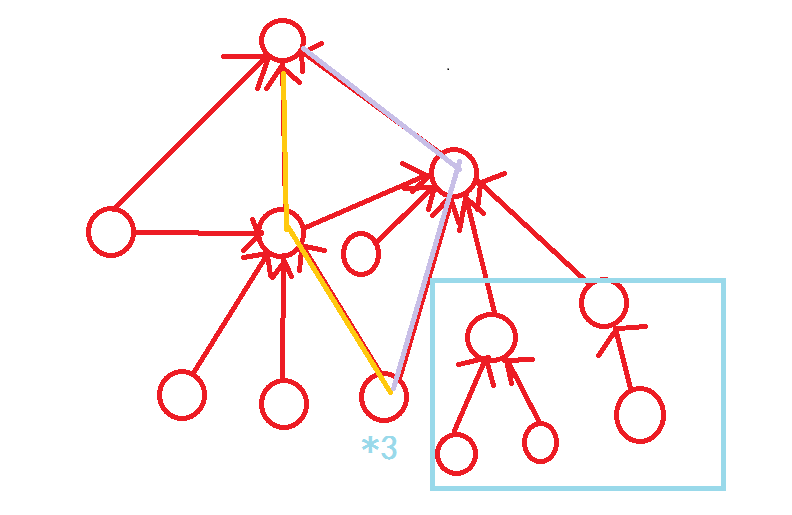
可以看出来,\(*3\)和\(*5\)操作,先算哪一个得到的整张图的乘积都是一样的,所以在乘积上,对于同一个操作,左右顺序不重要,只需要保证这个操作进行的时候子操作都进行完了就可以了。
(比如给出的例子操作里,蓝色框框里要先算最下面的三个点,得到上面的两个点的值,才能用这两个点向上面的一个点贡献\(*5\))
所有可以用拓补排序按入度为0加入队列的规则得到操作顺序。
然后按这个操作顺序每个点向连向的点贡献乘积即可。
对于没有被用到的操作,是不存在路径节点到\(m+1\)的,所有它的贡献是不会被累积到\(k\)里面的。
代码实现(写代码的时候我的边是从父操作到子操作,所有统计的是\(out\)):
inline void add(int u,int v)
{
out[u]++;G[u].push_back(v);F[v].push_back(u);
}
void Init()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lld",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;++i)
{
scanf("%d %d",&cz[i].op,&cz[i].x);
if(cz[i].op==1) scanf("%d",&cz[i].y);
else if(cz[i].op==3) for(int j=1,v;j<=cz[i].x;++j) scanf("%d",&v),add(i,v);
}
m++;
scanf("%d",&Q);
for(int i=1,v;i<=Q;++i) scanf("%d",&v),add(m,v);
}
void Topo()
{
int l=1;
for(int i=1;i<=m;++i)
if(!out[i]) tq[++tq[0]]=i;
while(l<=tq[0])
{
int u=tq[l++];
int S=F[u].size();
for(int i=0;i<S;++i)
if(!--out[F[u][i]]) tq[++tq[0]]=F[u][i];
}
}
void Update()
{
sum[m]=mul[m]=1;
for(int i=1;i<m;++i) sum[i]=(cz[i].op==2?cz[i].x:1);
for(int i=1;i<=tq[0];++i)
for(int j=0,S=F[tq[i]].size();j<S;++j)
sum[F[tq[i]][j]]=sum[F[tq[i]][j]]*sum[tq[i]]%mod;
for(int i=1;i<=n;++i) a[i]=a[i]*sum[m]%mod;
}
加法部分
如图,蓝色框框代表许多许多操作(2节点在1节点之前还有操作,3在2之前也还有操作,画上图太乱了就没画)。
假设2节点累积值是6,3节点累积值是10。
假设这里有个\(+5\)的操作,受到后面操作的影响,最后加上去的数会变成\(5*60+5*30+5*15\)。(蓝,绿,粉)。
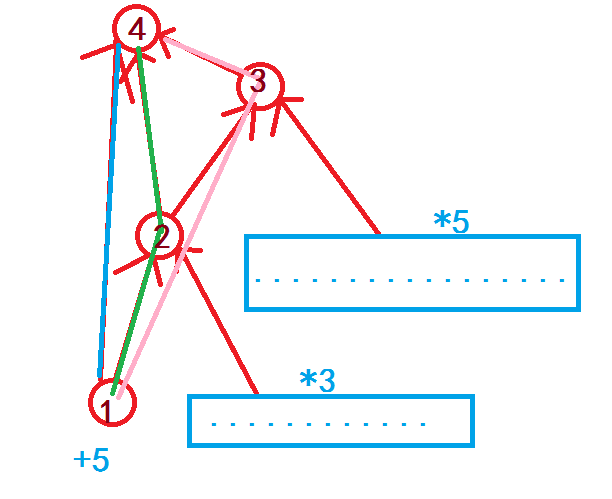
可以看出来,1直接连向4节点,这个时候23累积上去的乘积是60,所以1节点累加60。
1连向2节点,但2节点有两种。
2节点直接连向4节点,这时候3累积上的乘积是10,所以2节点累加10。
2节点是连向3节点,3节点连向4节点,无后续影响3节点,此时根节点的累积值是1,所以3累加1。这时候3节点后续有个\(*5\)影响2节点,此时累积到4的积是1,所以在2累加5。
所以2的累加值为\(10+5\)。
1在2这里会被\(*3\)影响,所以1的累加值是\(60+30+15\)。
这样会发现好像是一个递归的操作,但其实倒着想可以看成一个从上到下的下放操作,实现极其简单,代码非常短。
for(int i=tq[0];i;--i)
for(int j=G[tq[i]].size()-1,ml=1;j>=0;--j)
{
mul[G[tq[i]][j]]=((ll)ml*mul[tq[i]]+mul[G[tq[i]][j]])%mod;
ml=(ll)ml*sum[G[tq[i]][j]]%mod;
}
for(int i=1;i<=n;++i) a[i]=a[i]*sum[m]%mod;
for(int i=1;i<m;++i)
if(cz[i].op==1) a[cz[i].x]=(a[cz[i].x]+cz[i].y*mul[i])%mod;
放上完整代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
const ll mod=998244353;
int n,m,Q,out[N],tq[N];
ll a[N],mul[N],sum[N];
struct node{int op,x,y;}cz[N];
vector<int>G[N],F[N];
inline void add(int u,int v)
{
out[u]++;G[u].push_back(v);F[v].push_back(u);
}
void Init()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lld",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;++i)
{
scanf("%d %d",&cz[i].op,&cz[i].x);
if(cz[i].op==1) scanf("%d",&cz[i].y);
else if(cz[i].op==3) for(int j=1,v;j<=cz[i].x;++j) scanf("%d",&v),add(i,v);
}
m++;
scanf("%d",&Q);
for(int i=1,v;i<=Q;++i) scanf("%d",&v),add(m,v);
}
void Topo()
{
int l=1;
for(int i=1;i<=m;++i)
if(!out[i]) tq[++tq[0]]=i;
while(l<=tq[0])
{
int u=tq[l++];
int S=F[u].size();
for(int i=0;i<S;++i)
if(!--out[F[u][i]]) tq[++tq[0]]=F[u][i];
}
}
void Update()
{
sum[m]=mul[m]=1;
for(int i=1;i<m;++i) sum[i]=(cz[i].op==2?cz[i].x:1);
for(int i=1;i<=tq[0];++i)
for(int j=0,S=F[tq[i]].size();j<S;++j)
sum[F[tq[i]][j]]=sum[F[tq[i]][j]]*sum[tq[i]]%mod;
for(int i=tq[0];i;--i)
for(int j=G[tq[i]].size()-1,ml=1;j>=0;--j)
{
mul[G[tq[i]][j]]=((ll)ml*mul[tq[i]]+mul[G[tq[i]][j]])%mod;
ml=(ll)ml*sum[G[tq[i]][j]]%mod;
}
for(int i=1;i<=n;++i) a[i]=a[i]*sum[m]%mod;
for(int i=1;i<m;++i)
if(cz[i].op==1) a[cz[i].x]=(a[cz[i].x]+cz[i].y*mul[i])%mod;
}
int main()
{
Init();
Topo();
Update();
for(int i=1;i<=n;++i) printf("%lld ",a[i]);
}
[T4 贪吃蛇22)
如果蛇A吃了蛇B后,会被别的蛇吃掉,那他就不会吃B。那么假设所有蛇都不聪明,那么当被吃掉的蛇,假设为A,A吃过别的蛇,假设被A吃的是B,那么A当初就不会吃B,因为它吃了B后会被别的蛇吃掉。所以每个蛇吃别的蛇的时候,都储存一下如果这个蛇没有吃的话现在还剩了几条蛇,吃到第一条吃过别的蛇的蛇就返回这个的储存值。
可以用\(set\),平衡树来快速插入删除,但时间复杂度是A不了的,可以拿\(70pts\)左右。
正解思路与蚯蚓雷同。
每次被吃掉的蛇一定是没有吃过别的蛇的,就是在初始数组的蛇,所以被吃的蛇一定是递增,但不一定是严格递增。
另开一个数组q来储存A吃B之后的值。
假设上一次拿出来的蛇体力值为A,这次拿出来的是B,B一定小于等于A。
因为如果B不是由A-C得到的,且B比A大,那么上一次就该拿出B而不是A。如果B是由A-C得到的,由于\(C>0\),那么就一定有\(A>B\)。
所以每次拿出来吃别的蛇的蛇一定递减,但不一定严格递减。
假设上次是A吃B,这次是C吃D,按上述证明,就有\(A>=C,B<=D\),所以就可以得到\(A-B>=C-D\),即每次吃之后产生的值是具有单调性的(递减)。
那么计算的时候,每次最大的要么是q的要么是原始数组里的,每次最小的只能是原始数组的,如果q中的最小值比原始数组小,本次计算就结束了,返回储存值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号