b[i]=a[s[i]]类型题

显著特征

按顺序填入\(1\)到\(i\)的数组\(a\)，给定一个对应顺序\(s\)，新的数组\(b\)满足\(b[i]=a[s[i]]\)。（然后将新的b数组当成a数组，进行下一次相同的操作）

实质为：给定一个数n，将n拆分为\(n=x1+x2+x3+···xp\)，求有关\(lcm(x1,x2,x3,···，xp）\)的问题

终极题意为：从[2,n]的素数中，挑任意个素数，每个素数有任意个，使其加起来的和属于[1,n]，求一个问题。

代码写法:欧拉筛+DP

模板代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=数据范围+5;
int n,ans,dp[N],p[N];
bool vis[N];

signed main()
{
	cin>>n>>mod;
	for(int i=2;i<=n;++i)
	{
		if(!vis[i]) p[++p[0]]=i;
		for(int j=1;j<=p[0];++j)
		if(i*p[j]<=n) 
		{
			vis[i*p[j]]=1;	
			if(i%p[j]==0) break;
		}
	}
	
	dp[0]=1;
	
	for(int i=1;i<=p[0];++i)
	for(int j=n;j>=p[i];--j)
	for(int s=p[i];s<=j;s*=p[i])
	dp转移方程
	
	for(int i=0;i<=n;++i) ans=ans+dp[i];
	cout<<ans;
}

P4161（不同lcm的数量）

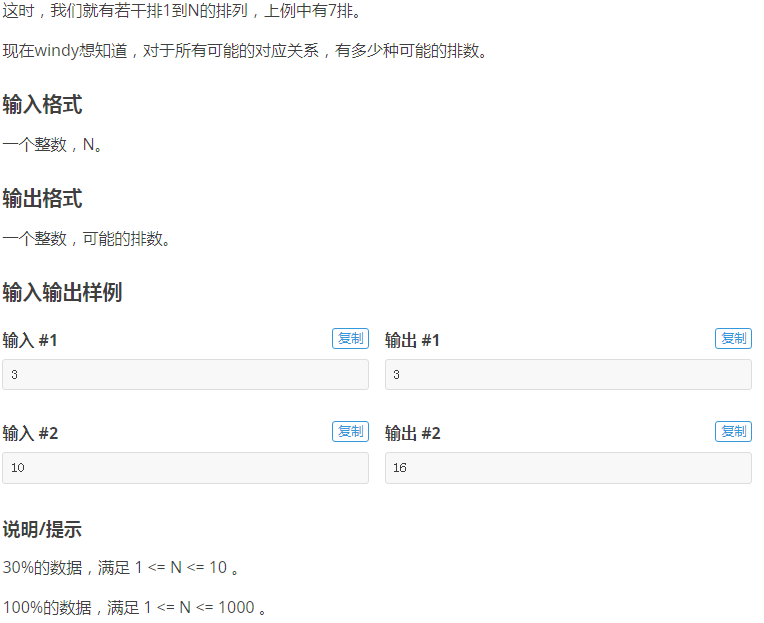
即：按顺序填入\(1\)到\(i\)的数组\(a\)，给定一个对应顺序\(s={2，3，1，5，4，6}\)，新的数组\(b\)满足\(b[i]=a[s[i]]\)

注意：在本题中实际条件是b[i]=s[a[i]]，但由于本题中初始数组下标和数的值相同，所以在第一次变化的时候就原本为下标为\(i\)的\(b\)得到了\(s[a[i]]\)的值，由于\(a[i]=i\)，所以第一次就相当于下标为\(i\)的\(b\)得到了\(s[i]\)的值，由于\(a[i]=i\)，所以\(a[s[i]]=s[i]\)，所以\(b[i]=a[s[i]]\)。

在第二次的时候，同理可知，原本为下标为\(i\)的\(b\)得到了\(s[a[i]]\)的值，由于\(a[i]=s[i]\)，即\(a\)数组等于\(s\)数组，所以第二次就相当于下标为\(i\)的\(b\)得到了\(a[s[i]]\)的值。

在第三次的时候，同理可知，原本为下标为\(i\)的\(b\)得到了\(s[a[i]]\)的值，由于\(a[i]=s[s[i]]\)，即，所以第二次就相当于下标为\(i\)的\(b\)得到了\(a[s[i]]\)的值。

（不会证明了，换个思路）

在原本给的模板题意中，\(b[i]=a[s[i]]\)，即将\(a\)数组按\(s[i]\)的顺序排个序，\(s[i]\)指下标。

在本题题意中，\(b[i]=s[a[i]]\)，即将\(a\)数组按\(s[i]\)的顺序排个序，\(s[i]\)指数值，但初始状态中\(a[i]=i\)，我们将排序看成数值和下标捆绑在一起排序，在这种情况下数值恒等于下标，那么就可以转换为给的模板题意。

正式解析

由给出的转换过程：

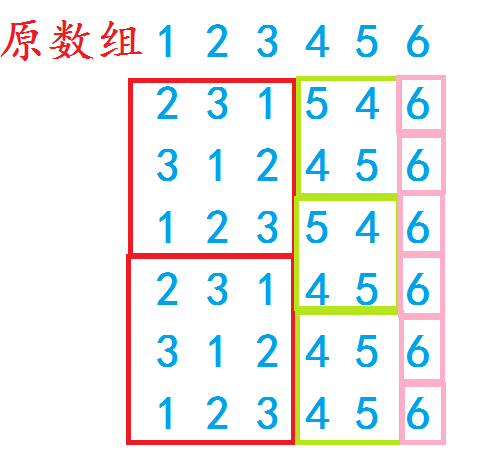
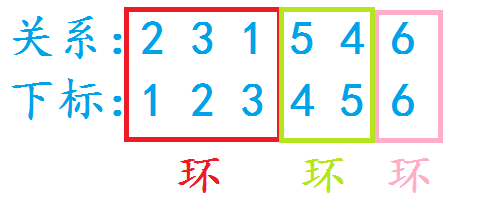
显而易见的：

第一个环长度为\(3\)，所以从\(123\)再到\(123\)需要3步。

第二个环长度为\(2\)，所以从\(45\)再到\(45\)需要2步。

第三个环长度为\(1\)，所以从\(6\)再到\(6\)需要1步。

而让所有环都跑回原状态，所需的步数是\(6=lca(3,2,1)\)。

（此处所说的环是指关系和下标所成的环）

所以本题的真实题意为：给定一个数n，将n拆分为\(n=x1+x2+x3+···xp\)，求有多少个不同的\(lcm(x1,x2,x3,···，xp）\)

这也是这种题的特征。

性质：

\(1.lcm(x,1)=x\)，所以只要有\(x<n\)，都可以通过补\(n-x\)个长度为1的环得到一个合法转移。

\(2.lcm(x,x)=x\)，所以在一组拆分里，如果有相同的\(x\)，其实只有一个\(x\)对答案有贡献，其余的\(x\)对答案是没有贡献的，和只有一个\(x\)其他\(x\)都拆分成长度为\(1\)的环时没有差别，所以只需要枚举不同的\(x\)。

\(3.lcm(x,y)=x*y/gcd(x,y)\)，所以当\(x,y\)扩大相同倍数时，答案和不扩大时是等效的。所以可以直接枚举素数，因为\(lcm(x,y)\)其实等于\(x,y\)中所含有的所有素数因子\(p\)，\(p\)的次幂取\(p\)在\(x,y\)中更大的一个，所有\(p\)乘起来的值。

由性质一：1对结果没影响，所以题目中给定一个数n，将n拆分为\(n=x1+x2+x3+···xp\)可变为从[2,n]中任意取数使和为[0,n]中的任意一数。

由性质二三可知，当\(d=gcd(x,y)\)时，\(lcm(x,y)=lcm(x,y/d)\)，但显而易见的\(x+y/d<=x+y\)，所以使所有的\(x\)满足\(gcd(xi,xj)=1\)时，在得到同样的\(lcm\)的情况下，此时的\(n=x1+x2+x3+···xp\)最小。

所以终极题意为：从[2,n]的素数中，挑任意个素数，每个素数有任意个，使其加起来的和属于[1,n]，请问有多少种挑选方案。

题意转换一下：有p[0]种物品，每种物品有无限个，每个物品占p[i]的空间，求\(∑f[s](s∈[0,n])\)，\(f\)为方案数。

于是这道题便成了一道背包问题。
值得注意的是，在DP部分代码是这样的：

	for(int i=1;i<=p[0];++i)
	for(int j=n;j>=p[i];--j)
	for(int s=p[i];s<=j;s*=p[i])
	dp[j]+=dp[j-s];

先处理包含\(p[i]\)后占j的空间的所有方案，这是为了保证在处理转移的时候,\(dp[j-s]\)中不含有包含\(p[i]\)的方案。

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e3+5;
int n,ans,dp[N],p[N];
bool vis[N];

signed main()
{
	cin>>n;
	for(int i=2;i<=n;++i)
	{
		if(!vis[i]) p[++p[0]]=i;
		for(int j=1;j<=p[0];++j)
		if(i*p[j]<=n) 
		{
			vis[i*p[j]]=1;	
			if(i%p[j]==0) break;
		}
	}
	
	dp[0]=1;
	
	for(int i=1;i<=p[0];++i)
	for(int j=n;j>=p[i];--j)
	for(int s=p[i];s<=j;s*=p[i])
	dp[j]+=dp[j-s];
	
	for(int i=0;i<=n;++i) ans+=dp[i];
	cout<<ans;
}

P6280（不同lcm的和）

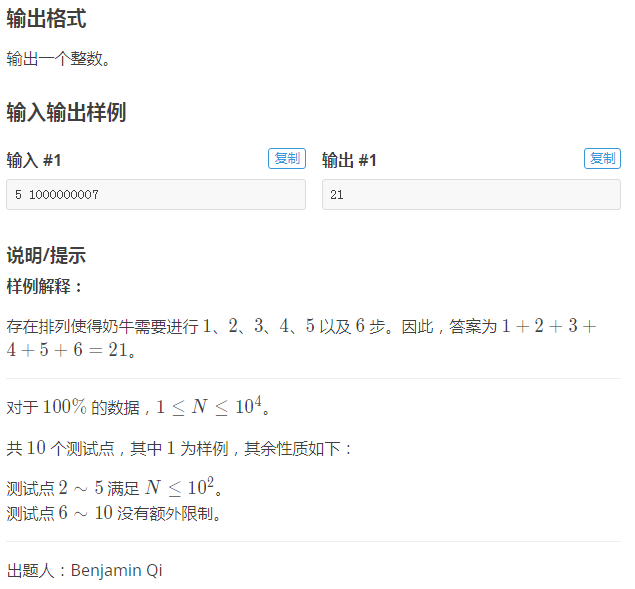
有了第一题的分析之后，我们可以很容易得到这道题的题意：给定一个数n，将n拆分为\(n=x1+x2+x3+···xp\)，求\(∑lcm(x1,x2,x3,···，xp）（lcm\)互不相同\()\)

终极题意：从\([2,n]\)的素数中，挑任意个素数，每个素数有任意个，使其加起来的和属于\([1,n]\)，求它们的乘积和。

设\(dp[i,j]\)表示前i个素数和为j时的乘积和，在加入第i+1个素数的时候，有\(dp[i,j]=dp[i-1,j-pow(p[i],k)]*pow(p[i],k)\)，倒着滚\(j\)维可以把\(dp\)的\(i\)维省略。

(插入数字x,就相当于在原本的每种分解式中加上一个大小为x的加数，所以对应的每种分解式的乘积也要乘上x，相当于所有方案的乘积和乘上一个x)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e4+5;
int n,ans,mod,dp[N],p[N];
bool vis[N];

signed main()
{
	cin>>n>>mod;
	for(int i=2;i<=n;++i)
	{
		if(!vis[i]) p[++p[0]]=i;
		for(int j=1;j<=p[0];++j)
		if(i*p[j]<=n) 
		{
			vis[i*p[j]]=1;	
			if(i%p[j]==0) break;
		}
	}
	
	dp[0]=1;
	
	for(int i=1;i<=p[0];++i)
	for(int j=n;j>=p[i];--j)
	for(int s=p[i];s<=j;s*=p[i])
	dp[j]=(dp[j]+dp[j-s]*s%mod)%mod;
	
	for(int i=0;i<=n;++i) ans=(ans+dp[i])%mod;
	cout<<ans;
}

Genijalac

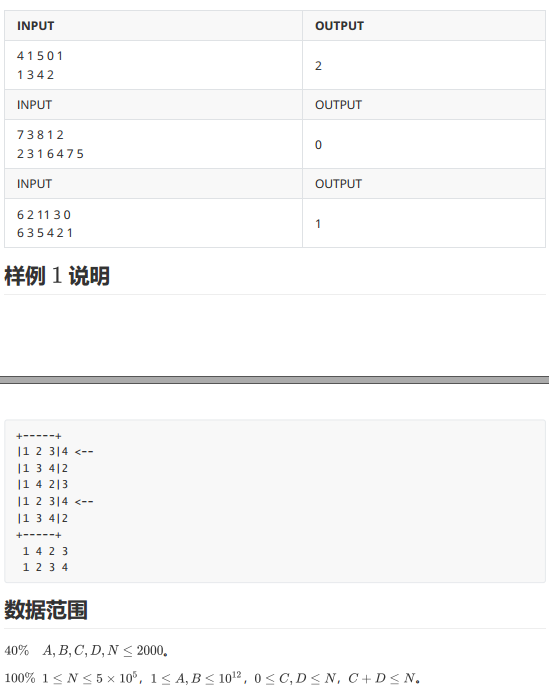
由解析一的图解我们可以知道，一个s所需的步数是所有环的lcm值，而本题多了一个左右切割的操作，意思就是，如果某个环全部在被切去的范围内，则对答案没有影响。

因为第一行本身就是答案，所以我们在查询的\(a,b\)都加上\(lcm-1\)，即把第一行前面添lcm-1行，补成一个完整的周期。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
int n,a,b,c,d,cnt,lcm=1,s[N];
bool vis[N];

void dfs(int x)
{
	cnt++;vis[x]=1;
	if(!vis[s[x]]) dfs(s[x]);
	else return;
}
inline int query(int x)
{
	return x/lcm;
}
signed main()
{
	freopen("genijalac.in","r",stdin);
	freopen("genijalac.out","w",stdout);
	
	scanf("%lld %lld %lld %lld %lld",&n,&a,&b,&c,&d);
	for(int i=1;i<=n;++i) scanf("%lld",&s[i]);
	
	for(int i=1+c;i<=n-d;++i)
	if(!vis[i]) cnt=0,dfs(i),lcm=lcm*cnt/__gcd(cnt,lcm);
	
	printf("%lld",query(b+lcm-1)-query(a+lcm-1-1));	
}