CDQ分治

CDQ分治

思想

分治，二分进行计算。将区间左半部分作为已知，右半部分作为查询进行计算。

陌上花开（三维偏序）

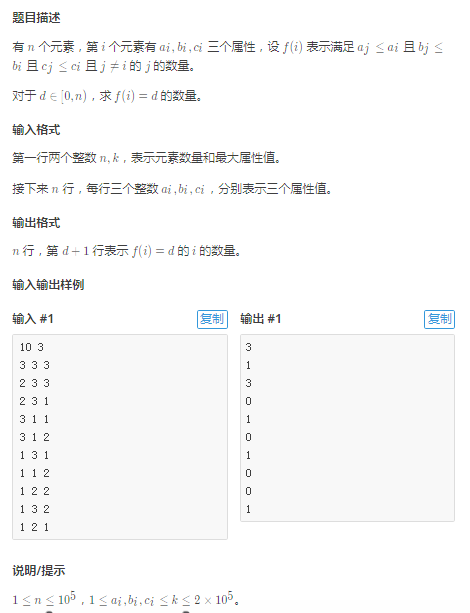
关键思想：按abc关键字进行排序，再以b为关键字进行归并排序。

因为先按a排序：每次归并时都一定有右区间的a大于等于左区间的a。

因为先按abc进行排序，故不会出现{1，1，3}{1，1，2}的尴尬情况。

因为对b进行归并排序：每次归并结束向上时，左右区间分别为一个递增序列。（不是也没关系，反正直接sort没有用正常归并操作。）

sort(b)的必要性：保证树状数组已经存储的c都满足对应的关键字b小于\(t[j].b\)。

归并求法导致每个区间的求值范围实际覆盖区间：

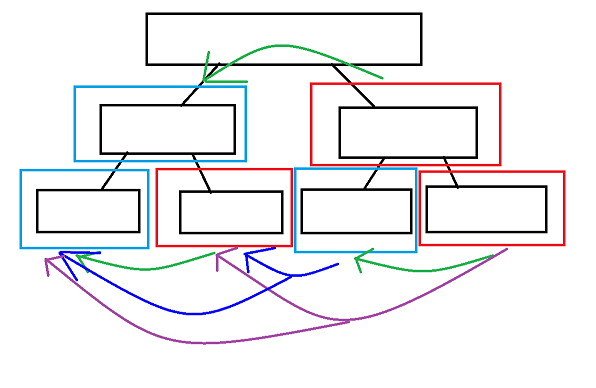
AC代码

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int n,kk,tt,s[N],c[N],ans[N];
struct e_
{
	int a,b,c;
	friend bool operator<(e_ a,e_ b)
	{
		return a.a<b.a||(a.a==b.a&&(a.b<b.b||(a.b==b.b&&a.c<b.c)));
	}
	friend bool operator!=(e_ a,e_ b)
	{
		return a.a^b.a||a.b^b.b||a.c^b.c;
	}
}e[N];
struct t_
{
	int v,b,c,val;
	
	friend bool operator<(t_ a,t_ b)
	{
		return (a.b==b.b&&a.c<b.c)||a.b<b.b;
	} 
}t[N];

void add(int x,int y)
{
	for(;x<=s[0];x+=x&-x) c[x]+=y;
}
int ask(int x)
{
	int res=0;
	for(;x;x-=x&-x) res+=c[x];
	return res;
}

void cdq(int l,int r)
{
	if(l==r) return;
	
	int m=(l+r)/2;
	
	cdq(l,m);
	cdq(m+1,r);

	sort(t+l,t+m+1);
	sort(t+m+1,t+r+1);
	
	int i=l,j=m+1;
	
	for(;j<=r;++j)
	{
		while(i<=m&&t[i].b<=t[j].b) add(t[i].c,t[i].v),++i;
		t[j].val+=ask(t[j].c);
	}
	
	for(;l<i;++l) add(t[l].c,-t[l].v);
}

int main()
{
	scanf("%d %d",&n,&kk);
	for(int i=1;i<=n;++i) 
	scanf("%d %d %d",&e[i].a,&e[i].b,&e[i].c),s[i]=e[i].c;
	
	sort(e+1,e+n+1);
	
	sort(s+1,s+n+1);
	s[0]=unique(s+1,s+n+1)-s-1;
	
	for(int i=1,j=0;i<=n;++i)
	if(e[i]!=e[j]) 
		j=i,t[++tt].v++,t[tt].b=e[i].b,t[tt].c=lower_bound(s+1,s+s[0]+1,e[i].c)-s;
	else t[tt].v++; 
	
	cdq(1,tt);
	
	for(int i=1;i<=tt;++i) ans[t[i].val+t[i].v-1]+=t[i].v;
	
	for(int i=0;i<n;++i) printf("%d\n",ans[i]);
}

所有用CDQ可解决的题都可以用KD_tree解决。

P3157动态逆序对

#include<bits/stdc++.h>

using namespace std;
#define ll long long
const int N=1e5+5,M=5e4+5;
int n,m,te,c[N],pos[N];
ll ans[M];
struct e_
{
	int x,k,pos,tim;
	friend bool operator<(e_ a,e_ b)
	{
		return a.pos<b.pos;
	}
}e[N+M];

inline void add(int x,int y)
{
	for(;x<=n;x+=x&-x) c[x]+=y;
}

inline int ask(int x)
{
	int res=0;
	for(;x;x-=x&-x) res+=c[x];
	return res;
}


void cdq(int l,int r)
{
	if(l==r) return;
	
	int mid=(l+r)>>1;
	
	cdq(l,mid);
	cdq(mid+1,r);
	
	sort(e+l,e+mid+1);
	sort(e+mid+1,e+r+1);
	
	int i=l,j=mid+1;
	//逆序对：i<j&&a[i]>a[j]，对于编号在x前的数，删掉x后少的逆序对为大于a[x]的数的个数 
	//从小到大排，就得到前面小于等于val的有x个，总数-x-1就是左边比它大的 
	for(;j<=r;++j)
	{
		while(i<=mid&&e[i].pos<=e[j].pos) add(e[i].x,e[i].k),++i;
		ans[e[j].tim]+=(ll)e[j].k*(ask(n)-ask(e[j].x)); 
	}
	for(--i;i>=l;--i) add(e[i].x,-e[i].k);

	i=mid,j=r;
	
	//逆序对：i<j&&a[i]>a[j]，对于编号在x后的数，删掉x后少的逆序对为小于a[x]的数的个数
	//从大到小排，相同原理得右边比它小的
	for(;j>mid;--j)
	{
		while(i>=l&&e[i].pos>=e[j].pos) add(e[i].x,e[i].k),--i;
		ans[e[j].tim]+=(ll)e[j].k*ask(e[j].x-1); 
	}
	for(++i;i<=mid;++i) add(e[i].x,-e[i].k);

}

int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1,val;i<=n;++i) scanf("%d",&val),pos[val]=i,e[++te]={val,1,i,0};
	for(int i=1,val;i<=m;++i) scanf("%d",&val),e[++te]={val,-1,pos[val],i};
	
	cdq(1,te);
	
	for(int i=1;i<m;++i) ans[i]+=ans[i-1];
	
	for(int i=0;i<m;++i) printf("%lld\n",ans[i]); 
}