RMQ问题
RMQ问题
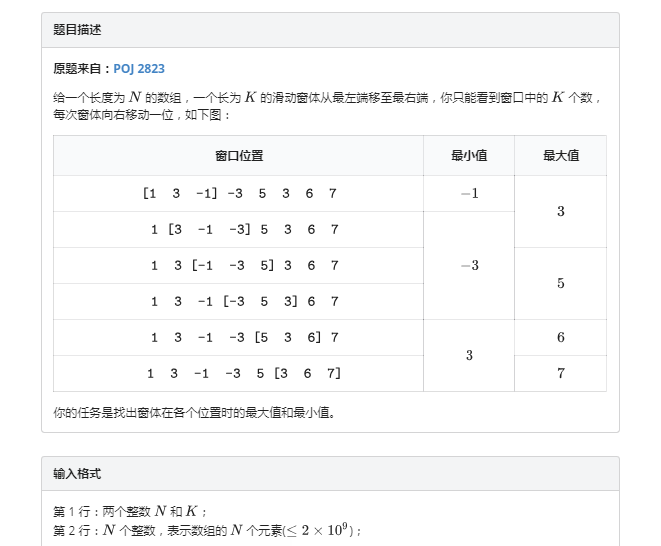
单调队列
单调队列
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m,a[N],q[N];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
int head=1,tail=0;
for(int i=1;i<m;++i)
{
while(head<=tail&&a[i]<=a[q[tail]]) tail--;
q[++tail]=i;
}
for(int i=m;i<=n;++i)
{
if(head<=tail&&i-q[head]>=m) head++;
while(head<=tail&&a[i]<=a[q[tail]]) tail--;
q[++tail]=i;
printf("%d ",a[q[head]]);
}
printf("\n");
head=1,tail=0;
for(int i=1;i<m;++i)
{
while(head<=tail&&a[i]>=a[q[tail]]) tail--;
q[++tail]=i;
}
for(int i=m;i<=n;++i)
{
if(head<=tail&&i-q[head]>=m) head++;
while(head<=tail&&a[i]>=a[q[tail]]) tail--;
q[++tail]=i;
printf("%d ",a[q[head]]);
}
}
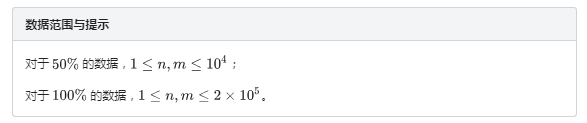
最大连续和

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=3e6+5;
ll n,a[N],b[N],s[N],q[N<<1];
bool vis[N];
int main()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>a[i]>>b[i],s[i]=s[i+n]=a[i]-b[i];
for(int i=1;i<=n*2;++i) s[i]+=s[i-1];
int head=1,tail=0;
for(int i=n*2;i>=0;--i)
{
if(head<=tail&&q[head]-i>n+1) head++;
if(i<n&&head<=tail&&s[q[head]]-s[i]>0) vis[i+1]=1;
while(head<=tail&&s[i]<=s[q[tail]]) tail--;
q[++tail]=i;
}
for(int i=1;i<=n;++i) s[i]=s[i+n]=a[i]-b[i];
for(int i=n*2;i>=0;++i) s[i]+=s[i+1];
head=1,tail=0;
for(int i=1;i<=n*2+1;++i)
{
if(head<=tail&&i-q[head]>n+1) head++;
if(i>n+1&&head<=tail&&s[q[head]]-s[i]>0) vis[i-n]=1;
while(head<=tail&&s[i]<=s[q[tail]]) tail--;
q[++tail]=i;
}
for(int i=1;i<=n;++i)
if(vis[i]) printf("TAK\n");
else printf("NIE\n");
}
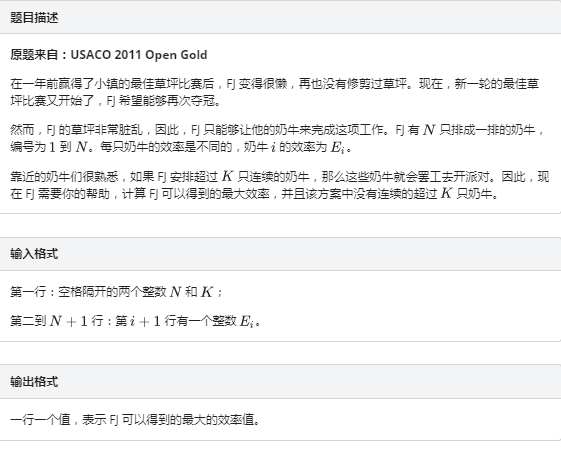
修剪草坪

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5;
int n,m;
ll f[N],sum[N];
int q[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> sum[i];
sum[i] += sum[i - 1];
}
int head = 0, tail = 0;
for(int i = 1; i <= n; i++){
if(i - q[head] > m && head <= tail)head++;
//不选第 i 个, 选第 i 个
f[i] = max(f[i - 1], f[q[head] - 1] - sum[q[head]] + sum[i]);
//维护f[i - x - 1] - s[i - x] 的单调递减行, 则队头的元素一定是最大的
while(head <= tail && f[q[tail] - 1] - sum[q[tail]] <= f[i - 1] - sum[i])tail--;
q[++tail] = i;
}
cout << f[n] << endl;
return 0;
}
最敏捷的机器人
【题目描述】Wind 设计了很多机器人。但是它们都认为自己是最强的,于是,一场比赛开始了……
机器人们都想知道谁是最敏捷的,于是它们进行了如下一个比赛。首先,他们面前会有一排共 n 个数,它们比赛看谁能最先把每连续 k 个数中最大和最小值写下来,当然,这些机器人运算速度都很快,它们比赛的是谁写得快。
但是 Wind 也想知道答案,你能帮助他吗?
【数据输入】第一行为 n,k,意义如题目描述。
第二行共 n 个数,为数字序列,所有数字均在 int 范围内,即所有数均为整数,且在 [−231,231−1]范围内。
【数据输出】共 n−k+1 行,第 i 行为第 i 至第 i+k−1 这 k 个数中的最大和最小值。
【输入样例】5 3
1 2 3 4 5
【输出样例】3 1
4 2
5 3
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,k,a[N],q1[N],q2[N];
int main()
{
scanf("%d %d",&n,&k);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
int l1=1,l2=1,r1=0,r2=0;
for(int i=1;i<k;++i)
{
while(l1<=r1&&a[i]>=a[q1[r1]]) r1--;
while(l2<=r2&&a[i]<=a[q2[r2]]) r2--;
q1[++r1]=q2[++r2]=i;
}
for(int i=k;i<=n;++i)
{
if(l1<=r1&&q1[l1]+k-1<i) l1++;
if(r2<=r2&&q2[l2]+k-1<i) l2++;
while(l1<=r1&&a[i]>=a[q1[r1]]) r1--;
while(l2<=r2&&a[i]<=a[q2[r2]]) r2--;
q1[++r1]=q2[++r2]=i;
printf("%d %d\n",a[q1[l1]],a[q2[l2]]);
}
}
旅行问题
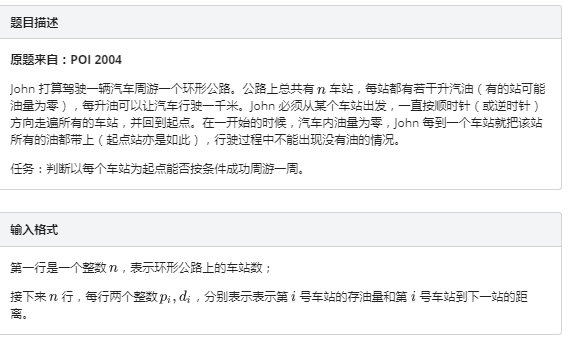

设:\(sum[i]=∑a[1—i]-b[1—i]\),则有\(sum[j]-sum[i-1]\)为从\(i\)到\(j\)的花费剩余,如果\(i\)可以走到\(i+n\),则必定有\(sum[i—i+n]-sum[i-1]>0\)。而当\(min(sum[i—i+n])-sum[i-1]>0\)时,该条件一定成立,故单调队列就只需要维护\(i—i+n\)的最小值
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
typedef long long ll;
int st[N], l, r;
int vis[N];
ll s[N];
int a[N], b[N];
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i];
s[i] = s[i + n] = a[i] - b[i]; //得到俩个点之间的权值
}
for(int i = 1; i <= 2 * n; i++) s[i] += s[i - 1];
l = 0;r = -1;
for(int i = 2 * n; i >= 0; i--)
{ //顺时针走,需要倒着求
if(st[l] >= i + n) l++; //维护n个车站
if(i < n)
{
if(s[st[l]]-s[i]>=0) vis[i + 1] = 1; //起点i + 1与 n 个车站内的最小前缀和进行比较, 判断是否可达
}
while(l <= r && s[i] <= s[st[r]]) r--;
st[++r] = i;
}
//翻转一下,逆时针方向走
b[0] = b[n];
for(int i = 1; i <= n; i++) s[i] = s[i + n] = a[i] - b[i - 1];
for(int i = 1; i <= 2 * n; i++) s[i] += s[i - 1];
l = 0;
r = -1;
for(int i = 1; i <= 2 * n; i++)
{
if(st[l] <= i - n)l++;
if(i > n)
{
if(s[i] >= s[st[l]])vis[i - n] = 1;
}
while(l <= r && s[st[r]] <= s[i])r--;
st[++r] = i;
}
for(int i = 1; i <= n; i++)
if(vis[i])printf("TAK\n");
else printf("NIE\n");
return 0;
}
【NOIP2011提】选择客栈(Day 1)
【题目描述】丽江河边有n家很有特色的客栈,客栈按照其位置顺序从1到n编号。每家客栈都按照某一种色调进行装饰(总共k种,用整数0~k-1表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。
两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过p。
他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过p元的咖啡店小聚。
【数据输入】每组输入数据共n+1行。
第一行三个整数n,k,p,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;
接下来的n行,第i+1行两个整数,之间用一个空格隔开,分别表示i号客栈的装饰色调和i号客栈的咖啡店的最低消费。
【数据输出】每组输出只有一行,一个整数,表示可选的住宿方案的总数。
【样例输入】 5 2 3
0 5
1 3
0 2
1 4
1 5
【样例输出】 3
2人要住同样色调的客栈,所有可选的住宿方案包括:住客栈①③,②④,②⑤,④⑤,但是若选择住4、5号客栈的话,4、5号客栈之间的咖啡店的最低消费是4,而两人能承受的最低消费是3元,所以不满足要求。因此只有前3种方案可选。
【数据规模】 对于30%的数据,有n≤100;
对于50%的数据,有n≤1,000;
对于100%的数据,有2≤n≤200,000,0<k≤50,0≤p≤100,0≤最低消费≤100。
#include<bits/stdc++.h>
using namespace std;
#define N 200005
int n,m,ans,p,pos;
int sum[N],pre[N],col[55];
int main()
{
scanf("%d %d %d",&n,&m,&p);
for(int i=1,x,y;i<=n;++i)
{
scanf("%d %d",&x,&y);
++x;
pre[i]=col[x];
col[x]=i;
sum[i]=sum[pre[i]]+1;
if(y<=p) pos=i;
for(int j=pre[i];j;j=pre[j])
if(j<=pos)
{
ans+=sum[j];
break;
}
}
printf("%d",ans);
}
ST算法
对于问题(RMQ,Random Maximum Query):给你一串固定、不修改的数字,询问多次某个区间内的最大值或者最小值。
用朴素的想法,依次遍历得到答案,时间复杂度为O(n),但是对于多次询问,如1E6次询问,这样的算法就不是最优的了。所以出现了ST算法。
ST算法的原理是动态规划,通过O(logn)的预处理dp数组,得到O(1)的询问。
1.预处理
假设dp[i,j]表示从a[i]到a[i+2j-1]这个范围内的最大值,即以a[i]为起点连续2j个数的最大值。
我们把它一分为二,每段元素都为2(j-1)个数字。也就是说dp[i,j]分为dp[i, j - 1]和f[i + 2j-1, j- 1]两部分(自己代入一下dp的定义)。
所以我们很容易得到状态转一方程\(dp[i][j] = max(dp[i][j - 1], dp[i + 2^(j-1)][j - 1])\);
我们在给\(dp[i][0]\)初始化一下均为a[i]。预处理完毕。
2.询问
先引入一个k值,每个区间均为2(k-1)个数字,所以两部分区间为[i, 2(k-1) + i -1]和[j - 2(k-1)+ 1,j]。显然必须要满足2个子区间能够完全覆盖[i , j],即要求\((2^(k-1)^ + i -1) + 1 >= (j - 2^(k-1)^ +1)\),易得2^k >= (j - i + 1),取k的最小值,使2个子区间尽可能的短。所以k = log2(j - i + 1);(向下取整)
所以对于每次询问易得\(ans = max(dp[i][k],dp[j - 2^k + 1][k])\)。
3.小技巧
cmath中log2函数效率较低,所以可以用递推处理log2d的值,我们用lo代表log2d向下取整的值,则lo[d] = lo[d/2]+1。
#include<bits/stdc++.h>
using namespace std;
const int N=2*1e5+5;
int n,m,l,r,f[N][20],lo[N];
int main()
{
scanf("%d",&n);
lo[0]=-1;
for(int i=1;i<=n;++i)
{
scanf("%d",&f[i][0]);
lo[i]=lo[i/2]+1;
}
for(int j=1;j<=lo[n];++j)
for(int i=1;i+(1<<j)-1<=n;++i)
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);
scanf("%d",&m);
while(m--)
{
scanf("%d %d",&l,&r);
int k=lo[r-l+1];
printf("%d\n",max(f[l][k],f[r-(1<<k)+1][k]));
}
}
【USACO 2007 Jan. Gold】Balanced Lineup
【题目描述】FJ 的 N 头牛总是按同一序列排队。有一天,FJ 决定让一些牛玩一场飞盘比赛。他准备找一群在对列中为置连续的牛来进行比赛,但是为了避免水平悬殊,牛的身高不应该相差太大。FJ 准备了 Q 个可能的牛的选择和所有牛的身高。他想知道每一组里面最高和最低的牛的身高差别。
【数据输入】第一行:N 和 Q;
第二至第 N+1 行,第 i+1 行是第 i 头牛的身高 hi ;
第 N+2 至第 N+Q+1 行,每行两个整数 A 和 B,表示从 A 到 B 的所有牛。
【数据输出】第一至第 Q 行,每行一个整数,表示对于询问的回答(即最高和最低的牛的身高差)。
【输入样例】6 3
1
7
3
4
2
5
1 5
4 6
2 2
【输出样例】6
3
0
【数据范围】对于全部数据,1≤N≤5×104,1≤Q≤1.8×105,1≤hi≤106,1≤A≤B≤N。
#include<bits/stdc++.h>
using namespace std;
const int N=50005;
int n,m,l,r,f[N][20],ff[N][20],lo[N];
int main()
{
scanf("%d %d",&n,&m);
lo[0]=-1;
for(int i=1;i<=n;++i)
{
scanf("%d",&f[i][0]);
ff[i][0]=f[i][0];
lo[i]=lo[i/2]+1;
}
for(int j=1;j<=lo[n];++j)
for(int i=1;i+(1<<j)-1<=n;++i)
{
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);
ff[i][j]=min(ff[i][j-1],ff[i+(1<<j-1)][j-1]);
}
while(m--)
{
scanf("%d %d",&l,&r);
int k=lo[r-l+1];
printf("%d\n",max(f[l][k],f[r-(1<<k)+1][k])-min(ff[l][k],ff[r-(1<<k)+1][k]));
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号