树上差分
树上差分
引理:差分序列的前缀和是原序列。
| 原数列 | 9 | 4 | 7 | 5 | 9 |
|---|---|---|---|---|---|
| 前缀和 | 9 | 13 | 20 | 25 | 34 |
| 差分数组 | 9 | -5 | 3 | -2 | 4 |
| 前缀和的差分数组 | 9 | 4 | 7 | 5 | 9 |
| 差分数组的前缀和 | 9 | 4 | 7 | 5 | 9 |
树上差分即将区间操作转化为路径操作。
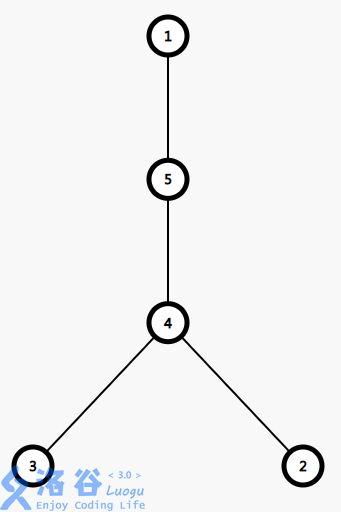
点差分
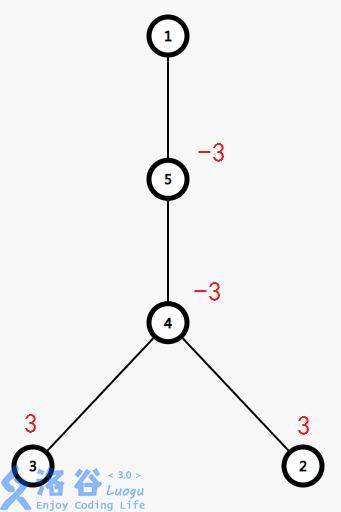
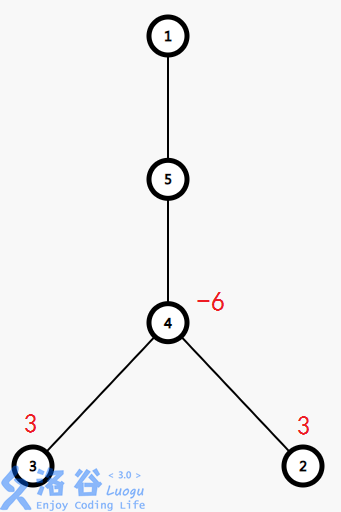
边差分
闇の連鎖
传说中的暗之连锁被人们称为 Dark。
Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。
经过研究,你发现 Dark 呈现无向图的结构,图中有 N 个节点和两类边,一类边被称为主要边,而另一类被称为附加边。
Dark 有 N – 1 条主要边,并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。
另外,Dark 还有 M 条附加边。
你的任务是把 Dark 斩为不连通的两部分。
一开始 Dark 的附加边都处于无敌状态,你只能选择一条主要边切断。
一旦你切断了一条主要边,Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。
但是你的能力只能再切断 Dark 的一条附加边。
现在你想要知道,一共有多少种方案可以击败 Dark。
注意,就算你第一步切断主要边之后就已经把 Dark 斩为两截,你也需要切断一条附加边才算击败了 Dark。
输入格式
第一行包含两个整数 N 和 M。
之后 N – 1 行,每行包括两个整数 A 和 B,表示 A 和 B 之间有一条主要边。
之后 M 行以同样的格式给出附加边。
输出格式
输出一个整数表示答案。
数据范围
N≤100000,M≤200000,数据保证答案不超过231−1
输入样例:
4 1
1 2
2 3
1 4
3 4
输出样例:
3
即从树上删除一条边和一条树外的边后,分成两个连通块。
首先,附加边的影响:
设附加边两端点为u,v,附加边会使u->v路径上任意一条边被删除,整棵树仍旧相连。
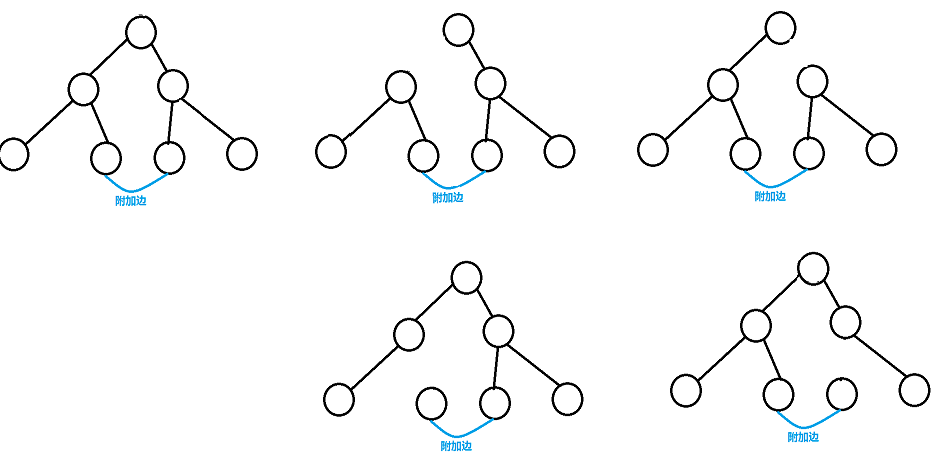
所以,当我们删除某条附加边时,对于LCA之后的点,还要注意有没有被别的附加边相连,设cnt数组为树上到v边受几条附加边影响,当\(cnt=1\)且受该条附加边影响时,删除这两条边可以使树分为两块。对于u->v之外的点,如果cnt=0,则删除这条边本来就可以直接让整棵树分为两块。
即:
\(cnt>0\)时表示删除该边整棵树仍旧相连
\(cnt=0\)时表示删除该边整棵树分为两块。
对于每条附加边,cnt=1则意味着删除这条附加边后,该边cnt=0,删除它后整棵树分为两块。
对于每个附加边cnt=0的点必然不会在附加边影响范围内,则直接统计加入附加边后cnt=0的边的总数\(total\),每个附加边的方案数\(=u->v\)上\(cnt=1\)的边数\(+total\)。
但是先求出所有边的LCA再对每条边进行找cnt太耗时间,所以我们可以优化一下:
设id数组为每条边的状态,每次LCA的时候同时查看id:
如果\(id=0\),即这条边没有被影响过,则方案数+1,id=1。
如果\(id=1\),即这条边被影响过,且还会被再影响一次,则将第一次影响时添加的方案数减去,则方案数-1,id=-1。
如果\(id=-1\),即这条边没有被影响过两次且已经删除过了,则直接跳过。
对于tot,因为我们选取了1做根节点,1只有出边没有入边,所以无需统计1的cnt(或者id)是否满足条件。
最后的答案就是\(ans+m*tot\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=2e5+5;
int n,m,te,tot,ans,tail[N],pre[N],dep[N],id[N];
struct e_
{
int v,pre;
}e[N*2];
inline void add(int u,int v)
{
e[++te]=(e_){v,tail[u]};
tail[u]=te;
}
void dfs(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(dep[v]) return;
dep[v]=dep[u]+1;
pre[v]=u;
dfs(v);
}
}
void lca(int u,int v,int p)
{
if(dep[u]<dep[v]) swap(u,v);
while(dep[u]>dep[v])
{
if(id[u]!=-1) id[u]?ans--,id[u]=-1:(id[u]=1,ans++);
u=pre[u];
}
while(u!=v)
{
if(id[u]!=-1) id[u]?ans--,id[u]=-1:(id[u]=1,ans++);
if(id[v]!=-1) id[v]?ans--,id[v]=-1:(id[v]=1,ans++);
u=pre[u];v=pre[v];
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v;i<n;++i)
{
scanf("%d %d",&u,&v);
add(u,v);
add(v,u);
}
dep[1]=1;
dfs(1);
for(int i=1,u,v;i<=m;++i)
{
scanf("%d %d",&u,&v);
lca(u,v,i);
}
for(int i=2;i<=n;++i)
if(!id[i]) tot++;
printf("%d\n",ans+tot*m);
}
雨天的尾巴
深绘里一直很讨厌雨天。
灼热的天气穿透了前半个夏天,后来一场大雨和随之而来的洪水,浇灭了一切。
虽然深绘里家乡的小村落对洪水有着顽固的抵抗力,但也倒了几座老房子,几棵老树被连根拔起,以及田地里的粮食被弄得一片狼藉。
无奈的深绘里和村民们只好等待救济粮来维生。
不过救济粮的发放方式很特别。
有 n 个点,形成一个树状结构。
有 m 次发放操作,每次选择两个点 x,y,对 x 到 y 的路径上(包括 x,y)的每个点发放一袋 z 类型的物品。
求完成所有发放操作后,每个点存放最多的是哪种类型的物品。
输入格式
第一行两个正整数n,m,含义如题目所示。
接下来n-1行,每行两个数(a,b),表示(a,b)间有一条边。
再接下来m行,每行三个数(x,y,z),含义如题目所示。
输出格式
共n行,第i行一个整数,表示第i座房屋里存放的最多的是哪种救济粮,如果有多种救济粮存放次数一样,输出编号最小的。
如果某座房屋里没有救济粮,则对应一行输出0。
数据范围
1≤n,m≤100000,
1≤z≤109
输入样例:
5 3
1 2
3 1
3 4
5 3
2 3 3
1 5 2
3 3 3
输出样例:
输出样例:
2
3
3
0
2
树上每个点添加值找众数。
对添加操作按z的值进行排序,对于z值相同的数看为一组,每组开始时都清空cnt数组,同时用ans和an储存原本数目最多的数和该数的个数。
朴素修改_60分:
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize(2)
const int N=1e5+5;
int n,m,te,tt,tot;
int tail[N],dep[N],pre[N],ans[N],an[N],cnt[N];
struct e_
{
int v,pre;
}e[N*2];
struct t_
{
int u,v,w;
friend bool operator<(t_ a,t_ b)
{
return a.w<b.w;
}
}t[N];
inline void add(int u,int v)
{
e[++te]=(e_){v,tail[u]};
tail[u]=te;
}
void dfs(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(dep[v]) continue;
dep[v]=dep[u]+1;
pre[v]=u;
dfs(v);
}
}
void lca(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
while(dep[u]>dep[v]) cnt[u]++,u=pre[u];
while(u!=v) cnt[u]++,cnt[v]++,u=pre[u],v=pre[v];
cnt[u]++;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v;i<n;++i)
{
scanf("%d %d",&u,&v);
add(u,v);
add(v,u);
}
dep[1]=1;
dfs(1);
for(int i=1;i<=m;++i)
scanf("%d %d %d",&t[i].u,&t[i].v,&t[i].w);
sort(t+1,t+m+1);
for(int i=1;i<=m;++i)
{
lca(t[i].u,t[i].v);
if(t[i].w!=t[i+1].w)
for(int j=1;j<=n;++j)
an[j]>=cnt[j]?cnt[j]=0:(ans[j]=t[i].w,an[j]=cnt[j],cnt[j]=0);
}
for(int i=1;i<=n;++i)
printf("%d\n",ans[i]);
}
优化操作
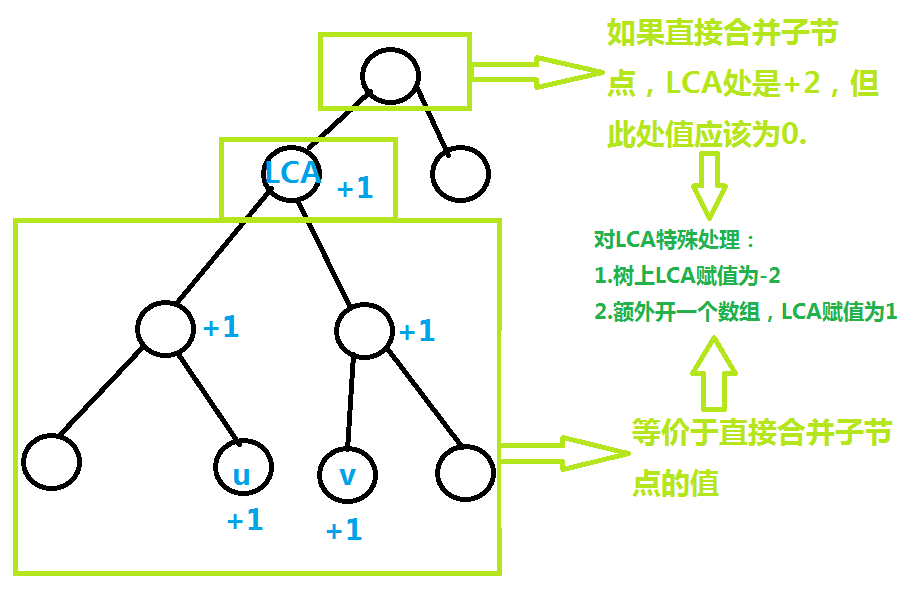
其实加了优化也只能拿个65:)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,te,tt;
int a[N],b[N],an[N],ans[N];
int f[N],st[N],tail[N],dep[N],tail2[N];
struct e_
{
int v,pre;
}e[N*2];
struct t_
{
int u,v,w,lca,preu,prev;
friend bool operator<(t_ a,t_ b)
{
return a.w<b.w;
}
}t[N];
inline void add(int u,int v)
{
e[++te]=(e_){v,tail[u]};
tail[u]=te;
}
void add_(int u,int v,int w)
{
t[++tt]=(t_){u,v,w,u==v?u:0,tail2[u],tail2[v]};
tail2[u]=tail2[v]=tt;
}
int find(int x)
{
return f[x]!=x?f[x]=find(f[x]):x;
}
void dfs(int u,int fa)
{
f[u]=u;
st[u]=1;
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);
}
for(int i=tail2[u];i;i=t[i].u==u?t[i].preu:t[i].prev)
{
int v=t[i].u==u?t[i].v:t[i].u;
if(!t[i].lca&&st[v]==2) t[i].lca=find(v);
}
f[u]=fa;
st[u]=2;
}
void dfs_(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==fa) continue;
dfs_(v,u);
a[u]+=a[v];
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v;i<n;++i)
{
scanf("%d %d",&u,&v);
add(u,v);
add(v,u);
}
for(int i=1,u,v,w;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&w);
add_(u,v,w);
}
dfs(1,0);
sort(t+1,t+m+1);
for(int i=1;i<=m;++i)
{
a[t[i].u]++;
a[t[i].v]++;
a[t[i].lca]-=2;
b[t[i].lca]++;
if(t[i].w!=t[i+1].w)
{
dfs_(1,-1);
for(int j=1;j<=n;++j)
a[j]+b[j]>an[j]?ans[j]=t[i].w,an[j]=a[j]+b[j],a[j]=b[j]=0:a[j]=b[j]=0;
}
}
for(int i=1;i<=n;++i)
printf("%d\n",ans[i]);
}
正解:树剖+线段树合并
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,Z=1e5,M=4e6+5,INF=1e9+5;
int n,m,ans[N];
int te,v[N<<1],pre[N<<1],tail[N];
int fa[N],top[N],dep[N],siz[N],son[N];
int ta,av[N<<2],aw[N<<2],ap[N<<2],at[N<<2];
int tot,lc[M],rc[M],root[N];
int val[M],id[M],rab[M];
inline void add(int x,int y)
{
++te;v[te]=y;pre[te]=tail[x];tail[x]=te;
}
inline void Dfs1(int x)
{
siz[x]=1;
for(int i=tail[x];i;i=pre[i])
if(v[i]!=fa[x])
{
fa[v[i]]=x;
dep[v[i]]=dep[x]+1;
Dfs1(v[i]);
siz[x]+=siz[v[i]];
if(siz[v[i]]>siz[son[x]]) son[x]=v[i];
}
}
inline void Dfs2(int x,int y)
{
top[x]=y;
if(!son[x]) return;
Dfs2(son[x],y);
for(int i=tail[x];i;i=pre[i])
if(v[i]!=fa[x]&&v[i]!=son[x]) Dfs2(v[i],v[i]);
}
inline int Lca(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
inline void Insert(int x,int y,int z)
{
if(!x) return;
++ta;av[ta]=y;aw[ta]=z;ap[ta]=at[x];at[x]=ta;
}
inline int New()
{
return rab[0]?rab[rab[0]--]:++tot;
}
inline void Update(int p)
{
if(val[lc[p]]>=val[rc[p]]) val[p]=val[lc[p]],id[p]=id[lc[p]];
else val[p]=val[rc[p]],id[p]=id[rc[p]];
}
inline void Modify(int l,int r,int x,int y,int &p)
{
if(!p) p=New();
if(l==r){val[p]+=y;id[p]=l;return;}
int mid=(l+r)>>1;
if(x<=mid) Modify(l,mid,x,y,lc[p]);
else Modify(mid+1,r,x,y,rc[p]);
Update(p);
if(!val[p]) id[p]=0;
}
inline void Throw(int p)
{
rab[++rab[0]]=p;
lc[p]=rc[p]=val[p]=id[p]=0;
}
inline int Merge(int l,int r,int u,int v)
{
if(!u||!v) return u|v;
int p=New(),mid=(l+r)>>1;
if(l==r)
{
val[p]=val[u]+val[v];
id[p]=l;
}
else
{
lc[p]=Merge(l,mid,lc[u],lc[v]);
rc[p]=Merge(mid+1,r,rc[u],rc[v]);
Update(p);
}
Throw(u);Throw(v);
return p;
}
inline void Dfs3(int x)
{
for(int i=tail[x];i;i=pre[i])
if(v[i]!=fa[x]) Dfs3(v[i]);
for(int i=at[x];i;i=ap[i])
Modify(1,Z,av[i],aw[i],root[x]);
ans[x]=id[root[x]];
if(fa[x]) root[fa[x]]=Merge(1,Z,root[fa[x]],root[x]);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,x,y;i<n;++i) scanf("%d %d",&x,&y),add(x,y),add(y,x);
Dfs1(1);Dfs2(1,1);
for(int i=1,u,v,tp;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&tp);
int lca=Lca(u,v);
Insert(u,tp,1);
Insert(v,tp,1);
Insert(lca,tp,-1);
Insert(fa[lca],tp,-1);
}
Dfs3(1);
for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
}
天天爱跑步
小C同学认为跑步非常有趣,于是决定制作一款叫作《天天爱跑步》的游戏。
《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一棵包含 n 个节点和 n-1 条边的树,任意两个节点存在一条路径互相可达。
树上节点的编号是 1~n 之间的连续正整数。
现在有 m 个玩家,第 i 个玩家的起点为 Si,终点为 Ti。
每天打卡任务开始时,所有玩家在第0秒同时从自己的起点出发,以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去,跑到终点后该玩家就算完成了打卡任务。
因为地图是一棵树,所以每个人的路径是唯一的。
小C想知道游戏的活跃度,所以在每个节点上都放置了一个观察员。
在节点 j 的观察员会选择在第 Wj 秒观察玩家,一个玩家能被这个观察员观察到当且仅当该玩家在第 Wj 秒也正好到达了节点 j。
小C想知道每个观察员会观察到多少人?
注意:我们认为一个玩家到达自己的终点后,该玩家就会结束游戏,他不能等待一段时间后再被观察员观察到。
即对于把节点 j 作为终点的玩家:若他在第 Wj 秒前到达终点,则在节点 j 的观察员不能观察到该玩家;若他正好在第 Wj 秒到达终点,则在节点 j 的观察员可以观察到这个玩家。
输入格式
第一行有两个整数 n 和 m 。
其中 n 代表树的结点数量, 同时也是观察员的数量, m 代表玩家的数量。
接下来 n-1 行每行两个整数 U 和 V ,表示结点 U 到结点 V 有一条边。
接下来一行 n 个整数,其中第个整数为Wj , 表示结点出现观察员的时间。
接下来 m 行,每行两个整数Si和Ti,表示一个玩家的起点和终点。
输出格式
一行 n 个整数,第 i 个整数表示结点 i 的观察员可以观察到多少人。
数据范围
1≤n,m≤3∗105
输入样例:
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
输出样例:
2 0 0 1 1 1
对于u->lca上的点x,\(d[u]-d[x]=w[x]\)时\(cnt[x]++\),即cnt[x]的值等于x的子树中的所有点u,满足\(d[x]+w[x]=d[u]\)的u的数量。
对于lca->v上的点x,\(d[u]-d[lca]+d[x]-d[lca]=w[x]\)时\(cnt[x]++\),即cnt[x]的值等于子树中满足\(d[x]-w[x]=2*d[lca]-d[u]\)的v的值。(即在每个v的位置存入\(2*d[lca]-d[u]\))
则采用差分,对于情况1,在u位置存入\(d[u]\),在\(lca\)的父节点删除\(d[u]\),在v位置存入\(2*d[lca]-d[u]\),在\(lca\)处删除\(2*d[lca]-d[u]\)。(两次删除位置不同是因为lca处必须至少有一个可统计的选择)
由于两次的判断条件不同,所以用两棵树同步进行差分操作。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m,te,w[N],d[N],ans[N],tail[N],f[N][22],c1[N*2],c2[N*2];
struct e_
{
int v,pre;
}e[N*2];
vector<int>a1[N],a2[N],b1[N],b2[N];
inline void add(int u,int v)
{
e[++te]=(e_){v,tail[u]};
tail[u]=te;
}
void dfs1(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==f[u][0]) continue;
d[v]=d[u]+1;
f[v][0]=u;
for(int j=1;(1<<j)<d[v];++j) f[v][j]=f[f[v][j-1]][j-1];
dfs1(v);
}
}
int lca_(int u,int v)
{
if(d[u]<d[v]) swap(u,v);
for(int j=20;j>=0;j--)
if(d[v]+(1<<j)<=d[u]) u=f[u][j];
if(u==v) return u;
for(int j=20;j>=0;j--)
if(f[u][j]!=f[v][j]) u=f[u][j],v=f[v][j];
return f[u][0];
}
void dfs2(int u)
{
int val=c1[d[u]+w[u]]+c2[d[u]-w[u]+n];
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==f[u][0]) continue;
dfs2(v);
}
for(int i=0;i<a1[u].size();++i) c1[a1[u][i]]++;
for(int i=0;i<b1[u].size();++i) c1[b1[u][i]]--;
for(int i=0;i<a2[u].size();++i) c2[a2[u][i]]++;
for(int i=0;i<b2[u].size();++i) c2[b2[u][i]]--;
ans[u]=c1[d[u]+w[u]]+c2[d[u]-w[u]+n]-val;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v;i<n;++i)
{
scanf("%d %d",&u,&v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;++i) scanf("%d",&w[i]);
d[1]=1;
dfs1(1);
for(int i=1,u,v;i<=m;++i)
{
scanf("%d %d",&u,&v);
int lca=lca_(u,v);
a1[u].push_back(d[u]);
b1[f[lca][0]].push_back(d[u]);
a2[v].push_back(2*d[lca]-d[u]+n);
b2[lca].push_back(2*d[lca]-d[u]+n);
}
dfs2(1);
for(int i=1;i<=n;++i) printf("%d ",ans[i]);
}
异象石
Adera是Microsoft应用商店中的一款解谜游戏。
异象石是进入Adera中异时空的引导物,在Adera的异时空中有一张地图。
这张地图上有N个点,有N-1条双向边把它们连通起来。
起初地图上没有任何异象石,在接下来的M个时刻中,每个时刻会发生以下三种类型的事件之一:
地图的某个点上出现了异象石(已经出现的不会再次出现);
地图某个点上的异象石被摧毁(不会摧毁没有异象石的点);
向玩家询问使所有异象石所在的点连通的边集的总长度最小是多少。
请你作为玩家回答这些问题。
输入格式
第一行有一个整数N,表示点的个数。
接下来N-1行每行三个整数x,y,z,表示点x和y之间有一条长度为z的双向边。
第N+1行有一个正整数M。
接下来M行每行是一个事件,事件是以下三种格式之一:
”+ x” 表示点x上出现了异象石
”- x” 表示点x上的异象石被摧毁
”?” 表示询问使当前所有异象石所在的点连通所需的边集的总长度最小是多少。
输出格式
对于每个 ? 事件,输出一个整数表示答案。
数据范围
1≤N,M≤105,
1≤x,y≤N,
x≠y,
1≤z≤109输入样例:
6
1 2 1
1 3 5
4 1 7
4 5 3
6 4 2
10
+ 3
+ 1
?
+ 6
?
+ 5
?
- 6
- 3
?
输出样例:
5
14
17
10
记录DFS序,连成一个环。对于每次添加删除操作,找出已有的石头里DFS序和现在这个石头相邻的两个石头,现在这个石头到另外两个石头的距离减去另外两个石头之间的距离就是改变的数值的两倍。
(也不知道为啥,反正是对的,先放着咯。)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
char dd;
const ll N=1e5+5;
ll n,m,te,ans,tot,tail[N],dfn[N],idf[N],dep[N],dis[N],f[N][22];
bool vis[N];
struct e_
{
ll v,w,pre;
}e[N*2];
set<ll>ex;
set<ll>::iterator it;
inline void add(ll u,ll v,ll w)
{
e[++te]=(e_){v,w,tail[u]};
tail[u]=te;
}
void dfs(ll u)
{
dfn[u]=++tot;
idf[tot]=u;
for(ll i=tail[u];i;i=e[i].pre)
{
ll v=e[i].v,w=e[i].w;
if(v==f[u][0]) continue;
dep[v]=dep[u]+1;
dis[v]=dis[u]+w;
f[v][0]=u;
for(ll j=1;(1<<j)<dep[v]&&j<=20;++j) f[v][j]=f[f[v][j-1]][j-1];
dfs(v);
}
}
ll lca(ll u,ll v)
{
if(dep[u]<dep[v]) swap(u,v);
for(ll j=20;j>=0;--j)
if(dep[v]+(1<<j)<=dep[u]) u=f[u][j];
if(u==v) return u;
for(ll j=20;j>=0;--j)
if(f[u][j]!=f[v][j]) u=f[u][j],v=f[v][j];
return f[u][0];
}
ll dist(ll u,ll v)
{
return dis[u]+dis[v]-2*dis[lca(u,v)];
}
void work()
{
ll u,x,y,z;
scanf("%d",&u);
x=dfn[u];
if(!vis[u]) ex.insert(x);
y=idf[(it=ex.lower_bound(x))==ex.begin()?*--ex.end():*--it];
z=idf[(it=ex.upper_bound(x))==ex.end()?*ex.begin():*it];
if(vis[u]) ex.erase(x);
ll d=dist(u,y)+dist(u,z)-dist(y,z);
if(!vis[u]) vis[u]=1,ans+=d/2;
else vis[u]=0,ans-=d/2;
}
int main()
{
scanf("%lld",&n);
for(ll i=1,u,v,w;i<n;++i)
{
scanf("%lld %lld %lld",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
dep[1]=1;
dfs(1);
scanf("%lld",&m);
while(m--)
{
cin>>dd;
if(dd=='?') printf("%lld\n",ans);
else work();
}
}
P2680 运输计划
给出一个含\(n\)个点的树和\(m\)条链,使树上任意一边权值为0,求链的长度最大值最小是多少。
二分答案加差分。
求出每条链的长度,然后排序,二分答案,大于mid的就在u,v分别+1,lca-2,表示这条链上的边要变,即在删除的边的候选集合内。dfs更新一下每条边有没有被覆盖,如果有一条边被覆盖了cnt次(cnt就是大于mid的所有链的总数)因为要把这些链都调整到mid的大小,就必须每条链都删边,如果一个边被覆盖了cnt次,并且距离最大的链减去这条边的长度小于等于mid就成立。
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m,te,tail[N],dep[N],sum[N],d[N],val[N],f[N][22];
struct e_
{
int v,w,pre;
}e[N<<1];
struct t_
{
int u,v,lca,dis;
friend bool operator<(t_ a,t_ b)
{
return a.dis>b.dis;
}
}t[N];
inline void read(int &x)
{
char dd=getchar();x=0;
while(dd<'0'||dd>'9') dd=getchar();
while(dd>='0'&&dd<='9') x=(x<<1)+(x<<3)+dd-'0',dd=getchar();
}
inline void add(int u,int v,int w)
{
e[++te]={v,w,tail[u]};
tail[u]=te;
}
void dfs1(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(v==f[u][0]) continue;
val[v]=w;
d[v]=d[u]+w;
dep[v]=dep[u]+1;
f[v][0]=u;
for(int j=1;(1<<j)<=dep[v]&&j<=20;++j) f[v][j]=f[f[v][j-1]][j-1];
dfs1(v);
}
}
int lca_(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
for(int j=20;j>=0;--j)
if(dep[v]+(1<<j)<=dep[u]) u=f[u][j];
if(u==v) return u;
for(int j=20;j>=0;--j)
if(f[u][j]!=f[v][j]) u=f[u][j],v=f[v][j];
return f[u][0];
}
void dfs2(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==f[u][0]) continue;
dfs2(v);
sum[u]+=sum[v];
}
}
bool check(int mid)
{
for(int i=1;i<=n;++i) sum[i]=0;
int cnt=0;
for(int i=1;i<=m;++i)
{
if(t[i].dis<=mid) break;
sum[t[i].u]++;
sum[t[i].v]++;
sum[t[i].lca]-=2;
cnt++;
}
dfs2(1);
for(int i=1;i<=n;++i)
if(sum[i]==cnt&&t[1].dis-val[i]<=mid) return 1;
return 0;
}
int main()
{
read(n);
read(m);
for(int i=1,u,v,w;i<n;++i) read(u),read(v),read(w),add(u,v,w),add(v,u,w);
dfs1(1);
for(int i=1,u,v;i<=m;++i)
{
read(t[i].u);
read(t[i].v);
t[i].lca=lca_(t[i].u,t[i].v);
t[i].dis=d[t[i].u]+d[t[i].v]-2*d[t[i].lca];
}
sort(t+1,t+m+1);
int l=0,r=t[1].dis;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1;
else l=mid+1;
}
printf("%d",r+1);
}
疫情控制
H 国有 n 个城市,这 n 个城市用 n-1 条双向道路相互连通构成一棵树,1号城市是首都,也是树中的根节点。
H 国的首都爆发了一种危害性极高的传染病。
当局为了控制疫情,不让疫情扩散到边境城市(叶子节点所表示的城市),决定动用军队在一些城市建立检查点,使得从首都到边境城市的每一条路径上都至少有一个检查点,边境城市也可以建立检查点。
但要注意的是,首都是不能建立检查点的。
现在,在H国的一些城市中已经驻扎有军队,且一个城市可以驻扎多个军队。
军队总数为 m 支。
一支军队可以在有道路连接的城市间移动,并在除首都以外的任意一个城市建立检查点,且只能在一个城市建立检查点。
一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度(单位:小时)。
请问:最少需要多少个小时才能控制疫情?
注意:不同的军队可以同时移动。
输入格式
第一行一个整数n,表示城市个数。
接下来的n-1行,每行3个整数,u、v、w,每两个整数之间用一个空格隔开,表示从城市u到城市v有一条长为w的道路,数据保证输入的是一棵树,且根节点编号为1。
接下来一行一个整数m, 表示军队个数。
接下来一行m个整数,每两个整数之间用一个空格隔开,分别表示这m个军队所驻扎的城市的编号。
输出格式
共一行,包含一个整数,表示控制疫情所需要的最少时间。如果无法控制疫情则输出-1。
数据范围
2≤m≤n≤300000,
0<w<109
输入样例:
4
1 2 1
1 3 2
3 4 3
2
2 2
输出样例:
3
简化题意:给定一棵树和M个已在树上的可移动的点,重新分配点的位置使可以从这些点到所有叶节点,并求出重新分配后的点的位置与初始位置的距离最小值。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=3e5+5;//log2(N)=18.1946
int n,m,te,tson,tail[N];
int F[N][20];
ll D[N][20];
bool vis[N];//驻守
struct son_
{
int s;ll d;
friend bool operator<(son_ x,son_ y){return x.d<y.d;}
}son[N];
struct e_
{
int v,pre;ll w;
}e[N<<1];
struct t_
{
int st,bl;
ll d,rest;
bool ari;
friend bool operator<(t_ x,t_ y){return x.d>y.d;}//d从大到小,rest从小到大 //初始位置,属于哪个子树,到根节点的距离 // 到达(军队到根节点)
}t[N];
inline void add(int u,int v,ll w)
{
e[++te]=(e_){v,tail[u],w};
tail[u]=te;
}
//预处理F,D
void dfs1(int u)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;ll w=e[i].w;
if(v==F[u][0]) continue;
F[v][0]=u;
D[v][0]=w;
for(int j=1;j<=18;++j)
if(F[F[v][j-1]][j-1]) F[v][j]=F[F[v][j-1]][j-1],D[v][j]=D[v][j-1]+D[F[v][j-1]][j-1];
else break;
dfs1(v);
}
}
//更新所在子树,更新到根节点距离
void update(int i)
{
int u=t[i].st;
for(int j=18;j>=0;--j) if(F[u][j]>1) t[i].d+=D[u][j],u=F[u][j];
t[i].bl=u;t[i].d+=D[u][0];
}
void update_(int i,ll V)
{
if(V>t[i].d) t[i].rest=V-t[i].d,t[i].ari=1;
else
{
t[i].ari=0;
int u=t[i].st;
for(int j=18;j>=0;--j) if(F[u][j]>1&&V>=D[u][j]) V-=D[u][j],u=F[u][j];
vis[u]=1;
}
}
void dfs2(int u,bool &bz)
{
if(e[tail[u]].pre==0){bz=0;return;}
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==F[u][0]||vis[v]) continue;
dfs2(v,bz);
if(!bz) return;
}
}
bool check(ll V)
{
for(int i=1;i<=n;++i) vis[i]=0;
for(int i=1;i<=m;++i) update_(i,V);
//判断是否需要跨根节点来驻扎
for(int i=1;i<=tson;++i)
if(!vis[son[i].s]) vis[son[i].s]=1,dfs2(son[i].s,vis[son[i].s]);
int j=1;
for(int i=1;i<=m;++i)
if(t[i].ari)
{
if(vis[t[i].bl]==0) vis[t[i].bl]=1;
else
{
while(j<=tson&&vis[son[j].s]) ++j;
if(j>tson) return 1;
if(t[i].rest>=son[j].d) vis[son[j].s]=1;
}
}
while(j<=tson&&vis[son[j].s]) ++j;
return j>tson;
}
int main()
{
scanf("%d",&n);
for(int i=1,u,v,w;i<n;++i) scanf("%d %d %d",&u,&v,&w),add(u,v,(ll)w),add(v,u,(ll)w);
for(int i=tail[1];i;i=e[i].pre)
{
int v=e[i].v;ll w=e[i].w;
son[++tson]=(son_){v,w};
F[v][0]=1;
D[v][0]=w;
dfs1(v);
}
scanf("%d",&m);
for(int i=1;i<=m;++i) scanf("%d",&t[i].st),update(i);
if(tson>m){printf("-1\n");return 0;}
sort(t+1,t+m+1);
sort(son+1,son+tson+1);
ll l=0,r=5e13;
while(l<=r)
{
ll mid=(l+r)>>1;
if(check(mid)) r=mid-1;
else l=mid+1;
}
printf("%lld",l);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号