最小生成树
最小生成树
Kruskal算法O(mlogm)
按边扫描,选边加入树,使每个子树都最小,一边加边一边合并,最后得到整棵树。
1.建立并查集,每个点个字构成一个集合。
2.将所有边按照w大小排序,依次扫描每条边(u,v,w)。
3.如果u,v属于同一集合(即相连,存在长度更小的使u和v相连的边),则跳过。
4.如果u,v不属于同一集合(即未相连,本边是使u和v相连的最小边),则合并集合,ans+=w。
5.所有边扫描完毕,在第四步运行的所有边即为该树的所有边,ans即是最小边权值总和。
struct t_
{
int u,v,w;
}t[N];
int find(int x)
{
return f[x]!=x?f[x]=find(f[x]):x;
}
bool cmp(t_ a,t_ b)
{
return a.w<b.w;
}
void Kruskal()
{
sort(t+1,t+m+1,cmp);
for(int i=1;i<=m;++i)
{
int x=find(t[i].u),y=find(t[i].v),w=t[i].w;
if(x==y) continue;
ans+=w;
f[y]=x;
}
}
走廊泼水节
给定一棵N个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。
注意: 树中的所有边权均为整数,且新加的所有边权也必须为整数。
输入格式
第一行包含整数t,表示共有t组测试数据。
对于每组测试数据,第一行包含整数N。
接下来N-1行,每行三个整数X,Y,Z,表示X节点与Y节点之间存在一条边,长度为Z。
输出格式
每组数据输出一个整数,表示权值总和最小值。
每个结果占一行。
数据范围
1≤N≤60001≤N≤6000
1≤Z≤1001≤Z≤100
输入样例:
2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5
输出样例:
4
17
由Kruskal可轻易想到,本题相当于删除了所有多余的连接u集合和v集合的边,只要我们每次合并u和v时,将多余的连接u集合,v集合的边还原即可。因为要保证wu,v是最短边,边的长度为整数且最小,所以我们先将所有的边按长度从小到大排序,每次扫描到一条边时进行合并u,v和还原剩余边的操作,还原的边长度为wu,v+1,则\(ans+=(w~u,v~+1)(siz[x]*siz[y]-1)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=6e3+5;
int tt,n,ans,te,f[N],siz[N];
struct t_
{
int u,v,w;
}t[N];
bool cmp(t_ a,t_ b)
{
return a.w<b.w;
}
int find(int x)
{
return f[x]!=x?f[x]=find(f[x]):x;
}
int main()
{
scanf("%d",&tt);
while(tt--)
{
ans=te=0;
scanf("%d",&n);
for(int i=1,u,v,w;i<n;++i)
{
f[i]=i;
siz[i]=1;
scanf("%d %d %d",&u,&v,&w);
t[++te]=(t_){u,v,w};
}
f[n]=n;
siz[n]=1;
sort(t+1,t+n,cmp);
for(int i=1;i<n;++i)
{
int x=find(t[i].u),y=find(t[i].v),w=t[i].w;
ans+=(w+1)*(siz[x]*siz[y]-1);
f[y]=x;
siz[x]+=siz[y];
}
printf("%d\n",ans);
}
}
野餐规划
一群小丑演员,以其出色的柔术表演,可以无限量的钻进同一辆汽车中,而闻名世界。
现在他们想要去公园玩耍,但是他们的经费非常紧缺。
他们将乘车前往公园,为了减少花费,他们决定选择一种合理的乘车方式,可以使得他们去往公园需要的所有汽车行驶的总公里数最少。
为此,他们愿意通过很多人挤在同一辆车的方式,来减少汽车行驶的总花销。
由此,他们可以很多人驾车到某一个兄弟的家里,然后所有人都钻进一辆车里,再继续前进。
公园的停车场能停放的车的数量有限,而且因为公园有入场费,所以一旦一辆车子进入到公园内,就必须停在那里,不能再去接其他人。
现在请你想出一种方法,可以使得他们全都到达公园的情况下,所有汽车行驶的总路程最少。
输入格式
第一行包含整数n,表示人和人之间或人和公园之间的道路的总数量。
接下来n行,每行包含两个字符串A、B和一个整数L,用以描述人A和人B之前存在道路,路长为L,或者描述某人和公园之间存在道路,路长为L。
道路都是双向的,并且人数不超过20,表示人的名字的字符串长度不超过10,公园用“Park”表示。
再接下来一行,包含整数s,表示公园的最大停车数量。
你可以假设每个人的家都有一条通往公园的道路。
输出格式
输出“Total miles driven: xxx”,其中xxx表示所有汽车行驶的总路程。
输入样例:
10
Alphonzo Bernardo 32
Alphonzo Park 57
Alphonzo Eduardo 43
Bernardo Park 19
Bernardo Clemenzi 82
Clemenzi Park 65
Clemenzi Herb 90
Clemenzi Eduardo 109
Park Herb 24
Herb Eduardo 79
3
输出样例:
Total miles driven: 183
精简版题意:给出n条边,求以节点1为根,根节点入度不超过s的最小生成树。
1.删除1节点,剩下的点可形成k个联通块。
2.求出每个联通块内部的最小生成树,即求出节点1的每个最小子树,在每个子树中选出一个点与1相连,使w1,v最小。
3.此时还剩下s-k个直接连节点1的位置,如图:
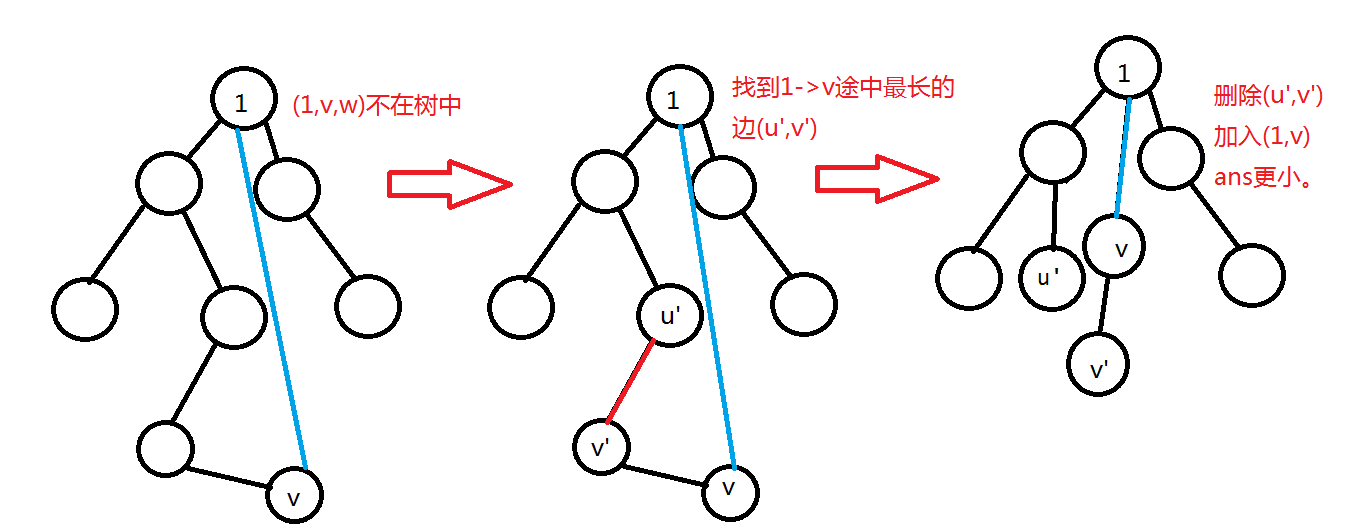
对于每次操作,我们都找出1到每个点的路上最长的边,然后朴素找差值最大的边进行删除加入。
#include<bits/stdc++.h>
using namespace std;
const int N=25;
int n,te,tot,tk,ans;
int f[N],st[N],dw[N][N];
bool ext[N][N];
struct e_
{
int u,v,w;
}e[N*N];
struct dis_
{
int u,v,w;
}dis[N];
map<string,int>name;
bool cmp(e_ a,e_ b)
{
return a.w<b.w;
}
int find(int x)
{
return f[x]!=x?f[x]=find(f[x]):x;
}
void Kruskal()
{
sort(e+1,e+te+1,cmp);
for(int i=1;i<=te;++i)
{
int x=find(e[i].u),y=find(e[i].v),w=e[i].w;
if(x==1||y==1||x==y) continue;
x<y?f[x]=y:f[y]=x;
ans+=w;
ext[e[i].u][e[i].v]=ext[e[i].v][e[i].u]=1;
}
for(int i=2;i<=tot;++i)
{
int ff=find(i);
if(dw[1][i]&&(!st[ff]||dw[1][i]<dw[1][st[ff]])) st[ff]=i;
if(f[i]==i) tk++,ans+=dw[1][st[i]],ext[1][st[i]]=ext[st[i]][1]=1;
}
}
void dfs(int u,int f)
{
for(int v=2;v<=tot;++v)
{
if(v==f||!ext[u][v]) continue;
if(dis[v].w==-1)
{
dis[v]=dis[u].w>dw[u][v]?dis[u]:(dis_){u,v,dw[u][v]};
dfs(v,u);
}
}
}
void change(int k)
{
while(k--)
{
memset(dis,-1,sizeof(dis));
dfs(1,-1);
int v,val=0;
for(int i=2;i<=tot;++i)
if(!ext[1][i]&&dw[1][i]&&dis[i].w-dw[1][i]>val) v=i,val=dis[i].w-dw[1][i];
if(val<=0) break;
ans-=val;
ext[dis[v].u][dis[v].v]=ext[dis[v].u][dis[v].v]=0;
ext[1][v]=ext[v][1]=1;
}
}
int main()
{
scanf("%d",&n);
name["Park"]=++tot;
f[tot]=tot;
for(int i=1;i<=n;++i)
{
int w;
string s1,s2;
cin>>s1>>s2;
scanf("%d",&w);
if(!name[s1]) name[s1]=++tot,f[tot]=tot;
if(!name[s2]) name[s2]=++tot,f[tot]=tot;
int u=name[s1],v=name[s2];
e[++te]=(e_){u,v,w};
e[++te]=(e_){v,u,w};
dw[u][v]=dw[v][u]=w;
}
Kruskal();
int s;
scanf("%d",&s);
change(s-tk);
printf("Total miles driven: %d\n",ans);
}
Prim算法O(mlogn)
与Dijkstra算法相似。
假设已经加入树的点属于集合T,未加入树的点的集合属于S,每次找到minx∈S,y∈T,即未加入树的点中,加入树距离最小的点,将该点加入树。
从已经加入树的节点中取点,扫描它的所有出边,更新别的端点。
void prim()
{
memset(d,0x3f,sizeof(d));
d[1]=0;
for(int i=1;i<n;++i)
{
int u=0;
for(int i=1;j<=n;++j)
if(!vis[j]&&d[j]<d[u]) u=j;
vis[u]=1;
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v,w=e[i].w;
if(!vis[v]&&d[v]>d[u]+w) d[v]=d[u]+w;
}
}
}
沙漠城堡
大卫大帝刚刚建立了一个沙漠帝国,为了赢得他的人民的尊重,他决定在全国各地建立渠道,为每个村庄提供水源。
与首都相连的村庄将得到水资源的浇灌。
他希望构建的渠道可以实现单位长度的平均成本降至最低。
换句话说,渠道的总成本和总长度的比值能够达到最小。
他只希望建立必要的渠道,为所有的村庄提供水资源,这意味着每个村庄都有且仅有一条路径连接至首都。
他的工程师对所有村庄的地理位置和高度都做了调查,发现所有渠道必须直接在两个村庄之间水平建造。
由于任意两个村庄的高度均不同,所以每个渠道都需要安装一个垂直的升降机,从而使得水能够上升或下降。
建设渠道的成本只跟升降机的高度有关,换句话说只和渠道连接的两个村庄的高度差有关。
需注意,所有村庄(包括首都)的高度都不同,不同渠道之间不能共享升降机。
输入格式
输入包含多组测试数据。
每组测试数据第一行包含整数N,表示村庄(包括首都)的总数目。
接下来N行,每行包含三个整数x,y,z,描述一个村庄的地理位置,(x,y)为该村庄的位置坐标,z为该村庄的地理高度。
第一个被描述的村庄即为首都。
当输入一行为0时,表示输入终止。
输出格式
每组数据输出一个结果,每个结果占一行。
结果为一个保留三位小数的实数,表示渠道的总成本和总长度的比值的最小值。
数据范围
2≤N≤1000,
0≤x,y<10000,
0≤z≤10000000
输入样例:
4
0 0 0
0 1 1
1 1 2
1 0 3
0
输出样例:
1.000
输出样例:
1.000
最小生成树,最小值乘积相除最小。
前置知识:01规划
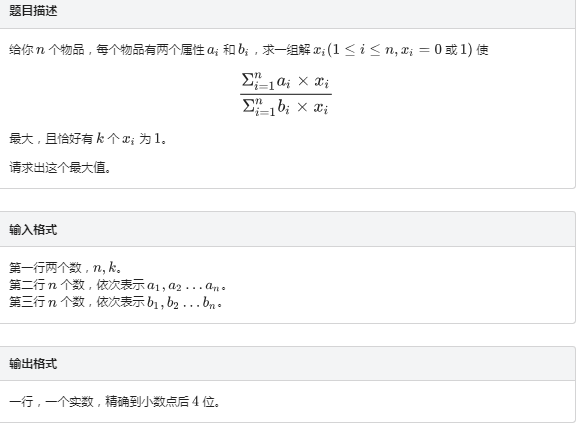
输入样例 1
5 3
1 2 4 1 2
4 3 9 3 7
输出样例 1
0.4667
输入样例 2
3 2
5 0 2
5 1 6
输出样例 2
0.8333
输入样例 3
10 6
1 5 3 7 2 8 5 4 2 6
15 35 12 12 9 15 7 7 13 15
输出样例 3
0.4923
题解:
设答案为L,则有
\(∑ai*xi/∑bi*xi>=L\)
\(∑ai*xi-L*∑bi*xi>=0\)
\(∑(ai-L*bi)*xi>=0\)
则二分找L,将单开一个数组储存\((ai-L*bi)\),由于要找大于0的,如果存在一组解满足有k个\(xi=1\)并且和大于等于0,则数组中最大的k个数加起来一定大于等于0,所以直接取从大到小排序后最大的k个数。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, k;
double a[N], b[N], c[N];
bool cmp(double a, double b) { return a > b; }
bool judge(double ans) {
for (int i = 1; i <= n; ++i) c[i] = a[i] - ans * b[i];
sort(c + 1, c + n + 1, cmp);
double res = 0;
for (int i = 1; i <= k; ++i) res += c[i];
return res >= 0;
}
int main() {
scanf("%d %d", &n, &k);
for (int i = 1; i <= n; ++i) scanf("%lf", &a[i]);
for (int i = 1; i <= n; ++i) scanf("%lf", &b[i]);
double l = 0, r = 1e5 + 5, rep = 0.000001;
while (r - l >= rep) {
double m = (l + r) / 2;
if (judge(m))
l = m + rep;
else
r = m - rep;
}
printf("%.4lf", l);
}
于是本题代码就出来了。
#include <bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define sqr(n) ((n)*(n))
using namespace std;
const int maxn = 1e3 + 5;
const double eps = 1e-6;
struct node{ int x,y,z; };
int n, v[maxn];
vector<node> ve;
double ans, e[maxn][maxn], dis[maxn];
void prim(double x)
{
rep (i, 1, n)
{
double mi = 2e9;
int now;
rep (j, 0, n - 1)
if(!v[j] && dis[j] < mi) mi = dis[j], now = j;
v[now] = 1;
ans += dis[now];
rep (j, 0, n - 1)
dis[j] = min(dis[j], abs(ve[now].z - ve[j].z) - x * e[now][j]);
}
}
bool judge(double x)
{
rep (i, 0, n - 1) dis[i] = 2e9, v[i] = 0;
dis[0] = 0; ans = 0;
prim(x);
return ans > 0;
}
int main()
{
while (cin >> n, n)
{
vector<node>().swap(ve);
for (int i = 1, x, y, z; i <= n; ++i)
{
scanf("%d %d %d",&x,&y,&z);
ve.push_back(node{x, y, z});
}
rep (i, 0, n - 1)
rep (j, 0, n - 1)
e[i][j] = sqrt(0.0 + sqr(ve[i].x - ve[j].x) + sqr(ve[i].y - ve[j].y));
double l = 0, r = 2e9;
while(r - l > eps)
{
double mid = (l + r) / 2;
if(judge(mid)) l = mid;
else r = mid;
}
printf("%0.3f\n", r);
}
return 0;
}
黑暗城堡
在顺利攻破Lord lsp的防线之后,lqr一行人来到了Lord lsp的城堡下方。
Lord lsp黑化之后虽然拥有了强大的超能力,能够用意念力制造建筑物,但是智商水平却没怎么增加。
现在lqr已经搞清楚黑暗城堡有N个房间,M条可以制造的双向通道,以及每条通道的长度。
lqr深知Lord lsp的想法,为了避免每次都要琢磨两个房间之间的最短路径,Lord lsp一定会把城堡修建成树形的。
但是,为了尽量提高自己的移动效率,Lord lsp一定会使得城堡满足下面的条件:
设 D[i] 为如果所有的通道都被修建,第 i 号房间与第1号房间的最短路径长度;而 S[i] 为实际修建的树形城堡中第 i 号房间与第1号房间的路径长度;要求对于所有整数 i,有 S[i]=D[i] 成立。
为了打败Lord lsp,lqr想知道有多少种不同的城堡修建方案。
你需要输出答案对 231–1 取模之后的结果。
输入格式
第一行有两个整数 N 和 M。
之后 M 行,每行三个整数X,Y 和L,表示可以修建 X 和 Y 之间的一条长度为 L 的通道。
输出格式
一个整数,表示答案对 231–1 取模之后的结果。
数据范围
2≤N≤1000,
N−1≤M≤N(N−1)/2,
1≤L≤100
输入样例:
3 3
1 2 2
1 3 1
2 3 1
输出样例:
2
由题可知,即给出n个点m条边求最小生成树的组成方案有多少。
那么只需要在Prim的基础上增加一个sum数组,记录有几个点可以到v,最后把sum数组累乘就好了。
结合图示:

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e3+5,p=(1<<31)-1;
ll ans=1,sum[N];
int n,m,d[N];
bool vis[N];
struct t_
{
int v,w;
};
deque<t_>nxt[N];
void Prim()
{
memset(d,0x3f,sizeof(d));
d[1]=0;
sum[1]=1;
for(int k=1;k<n;++k)
{
int u=0;
for(int i=1;i<=n;++i)
if(!vis[i]&&d[i]<d[u]) u=i;
vis[u]=1;
for(int i=0;i<nxt[u].size();++i)
{
int v=nxt[u][i].v,w=nxt[u][i].w;
if(!vis[v])
{
if(d[v]==d[u]+w) sum[v]++;
else
if(d[v]>d[u]+w) d[v]=d[u]+w,sum[v]=1;
}
}
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v,w;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&w);
nxt[u].push_back((t_){v,w});
nxt[v].push_back((t_){u,w});
}
Prim();
for(int i=1;i<=n;++i)
ans=(ans*sum[i])%p;
printf("%d",ans);
}
最小生成树计数
#include<bits/stdc++.h>
using namespace std;
#define u(i) e[i].u
#define v(i) e[i].v
#define w(i) e[i].w
#define l(i) a[i].l
#define r(i) a[i].r
#define v(i) a[i].v
const int N=105,M=1e3+5,mod=31011;
int n,m,cnt,tot,ans=1,sum;
int fa[N];
struct E_
{
int u,v,w;
friend bool operator<(E_ a,E_ b)
{
return a.w<b.w;
}
}e[M];
struct A_{int l,r,v;}a[M];
int find(int x)
{
return fa[x]!=x?fa[x]=find(fa[x]):x;
}
void dfs(int x,int now,int k)
{
if(now==r(x)+1)
{
if(k==v(x)) sum++;
return;
}
int x=find(u(now)),y=find(v(now));
if(x!=y)
{
fa[x]=y;
dfs(x,now+1,k+1);
fa[x]=x;fa[y]=y;
}
dfs(x,now+1,k);
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=1;i<=m;++i) scanf("%d %d %d",&u(i),&v(i),&w(i));
soer(e+1,e+m+1);
for(int i=1;i<=m;++i)
{
if(w(i)!=w(i-1)){r(cnt)=i-1;l(++cnt)=i;}
int x=find(u(i)),y=find(v(i));
if(x!=y) {fa[x]=y;v(i)++;tot++;}
}
r(cnt)=m;
if(tot!=n-1){printf("0");return 0;}
for(int i=1;i<=n;++i) fa[i]=i;
for(int i=1;i<=cnt;++i)
{
sum=0;
dfs(i,l(i),0);
ans=(ans*sum)%mod;
for(int j=l(i);j<=r(i);++j)
{
int x=find(u(j)),y=find(y(i));
if(x!=y) return fa[x]=y;
}
}
printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号