树形DP
树形DP
没有上司的舞会
Ural大学有N名职员,编号为1~N。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 Hi 给出,其中 1≤i≤N。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有
参会职员的快乐指数总和最大,求这个最大值。
输入格式
第一行一个整数N。
接下来N行,第 i 行表示 i 号职员的快乐指数Hi。
接下来N-1行,每行输入一对整数L, K,表示K是L的直接上司。
输出格式
输出最大的快乐指数。
数据范围
1≤N≤6000,
128≤Hi≤127
输入样例:
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
输出样例:
输出样例:
5
每个人只有两种状态,则设dp[0][i]dp[0][i]为第ii个人不来,他的下属所能获得的最大快乐值;dp[1][i]dp[1][i]为第ii个人来,他的下属所能获得的最大快乐值。
所以容易推出状态转移方程:
\(dp[0][i]=∑~u=sons~max(dp[1][u],dp[0][u])\)当前节点不选,那么子节点随意
\(dp[1][i]=∑~u=sons~dp[0][u]+happy[i]\)当前节点选,子节点不能选
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3ffffff
#define maxn 6005
int n,root,h[maxn],f[2][maxn];
deque<int>s[maxn];
bool vis[maxn];
void dfs(int x)
{
f[0][x]=0;
f[1][x]=h[x];
for(int i=0;i<s[x].size();++i)
{
int v=s[x][i];
dfs(v);
f[0][x]+=max(f[1][v],f[0][v]);
f[1][x]+=f[0][v];
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&h[i]),f[0][i]=f[1][i]=-INF;
for(int i=1,a,b;i<n;++i)
{
scanf("%d %d",&a,&b);
s[b].push_back(a);
vis[a]=1;
}
for(int i=1;i<=n;++i)
if(!vis[i])
{
root=i;
break;
}
dfs(root);
printf("%d",max(f[0][root],f[1][root]));
}
选课
学校实行学分制。
每门的必修课都有固定的学分,同时还必须获得相应的选修课程学分。
学校开设了 N 门的选修课程,每个学生可选课程的数量 M 是给定的。
学生选修了这 M 门课并考核通过就能获得相应的学分。
在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其他的一些课程的基础上才能选修。
例如《Windows程序设计》必须在选修了《Windows操作基础》之后才能选修。
我们称《Windows操作基础》是《Windows程序设计》的先修课。
每门课的直接先修课最多只有一门。
两门课可能存在相同的先修课。
你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修条件。
假定课程之间不存在时间上的冲突。
输入格式
输入文件的第一行包括两个整数N、M(中间用一个空格隔开)其中1≤N≤300,1≤M≤N。
接下来N行每行代表一门课,课号依次为1,2,…,N。
每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。
学分是不超过10的正整数。
输出格式
输出一个整数,表示学分总数。
输入样例:
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
输出样例:
13
#include<bits/stdc++.h>
using namespace std;
#define maxn 305
int n,m,f[maxn][maxn],a[maxn];
deque<int>q[maxn];
void dfs(int x)
{
for(int i=1;i<=m;++i) f[x][i]=a[x];
for(int i=0;i<q[x].size();++i)
{
int y=q[x][i];
dfs(y);
for(int j=m;j>=1;--j)
for(int k=1;k<j;++k)
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
}
}
void dfss(int x)
{
for(int i=0;i<q[x].size();++i)
{
int y=q[x][i];
dfs(y);
for(int j=m;j>=0;--j)
for(int k=1;k<=j;++k)
f[x][j]=max(f[x][j],f[x][j-k]+f[y][k]);
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,x;i<=n;i++)
{
scanf("%d %d",&x,&a[i]);
q[x].push_back(i);
}
dfss(0);
printf("%d",f[0][m]);
}
积蓄程度(二次扫描和换根法)
有一个树形的水系,由 N-1 条河道和 N 个交叉点组成。
我们可以把交叉点看作树中的节点,编号为 1~N,河道则看作树中的无向边。
每条河道都有一个容量,连接 x 与 y 的河道的容量记为 c(x,y)。
河道中单位时间流过的水量不能超过河道的容量。
有一个节点是整个水系的发源地,可以源源不断地流出水,我们称之为源点。
除了源点之外,树中所有度数为 1 的节点都是入海口,
可以吸收无限多的水,我们称之为汇点。
也就是说,水系中的水从源点出发,沿着每条河道,最终流向各个汇点。
在整个水系稳定时,每条河道中的水都以单位时间固定的水量流向固定的方向。
除源点和汇点之外,其余各点不贮存水,也就是流入该点的河道水量之和等于从该点流出的河道水量之和。
整个水系的流量就定义为源点单位时间发出的水量。在流量不超过河道容量的前提下,求哪个点作为源点时,整个水系的流量最大,输出这个最大值。
输入格式
输入第一行包含整数T,表示共有T组测试数据。
每组测试数据,第一行包含整数N。
接下来N-1行,每行包含三个整数x,y,z,表示x,y之
间存在河道,且河道容量为z。
节点编号从1开始。
输出格式
每组数据输出一个结果,每个结果占一行。
数据保证结果不超过231-1。
数据范围
N≤231-1
输入样例:
1
5
1 2 11
1 4 13
3 4 5
4 5 10
输出样例:
输出样例:
26
D[x]表示以x为根的子树中把x作为源点,从x流向子树的流量
D[x]=∑y∈son(x)【if(y的度数>1)】,c(x,y)【if(y的度数=1)】
#include<bits/stdc++.h>
using namespace std;
#define maxn 200005
int t,n,ans,tot;
int d[maxn],f[maxn],tail[maxn],dep[maxn];
bool vis[maxn];
struct op
{
int v,w,pre;
}eg[maxn*2];
void add(int u,int v,int w)
{
eg[++tot].v=v;
eg[tot].w=w;
eg[tot].pre=tail[u];
tail[u]=tot;
dep[u]++;
}
void dp(int u)
{
vis[u]=1;
for(int i=tail[u];i;i=eg[i].pre)
{
int v=eg[i].v,w=eg[i].w;
if(vis[v]) continue;
if(dep[v]==1) d[u]+=w;
else {dp(v);d[u]+=min(d[v],w);}
}
}
void dfs(int u)
{
vis[u]=1;
for(int i=tail[u];i;i=eg[i].pre)
{
int v=eg[i].v,w=eg[i].w;
if(vis[v]) continue;
if(dep[u]==1) f[v]=d[v]+w;
else f[v]=d[v]+min(w,f[u]-min(w,d[v]));
dfs(v);
}
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
memset(vis,0,sizeof(vis));
memset(d,0,sizeof(d));
memset(tail,0,sizeof(tail));
memset(dep,0,sizeof(dep));
memset(f,0,sizeof(f));
tot=0;
for(int i=1,a,b,c;i<n;++i)
{
scanf("%d %d %d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dp(1);
memset(vis,0,sizeof(vis));
f[1]=d[1];
dfs(1);
ans=0;
for(int i=1;i<=n;++i) ans=max(ans,f[i]);
printf("%d\n",ans);
}
}
战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
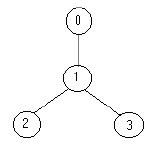
只需要放置1名士兵(在节点1处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数N,表示树的节点数目。
接下来N行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从0到N-1,每个节点的子节点数量均不超过10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
0<N≤15000<N≤1500
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
状态可以表示为\(f[i][j]\)
\(f[i][0]\)表示不选当前结点
\(f[i][1]\)表示选择当前结点
因为每条边都要被观察到
所以父结点不选子节点一定要选
父结点选子节点可以选或不选
表示为转移方程就是
\(f[u][0] += f[v][1]\)
\(f[u][1] += min(f[v][1],f[v][0])\)
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 1510,M = N * 2,inf = 0x3f3f3f3f;
int n,f[N][2];
int head[N],nxt[M],ver[M],idx;
bool st[N];
void add(int u,int v)
{
nxt[++ idx] = head[u];
ver[idx] = v;
head[u] = idx;
}
void dfs(int u)
{
f[u][0] = 0;
f[u][1] = 1;
for(int i = head[u]; i ;i = nxt[i])
{
int v = ver[i];
dfs(v);
f[u][1] += min(f[v][0],f[v][1]);
f[u][0] += f[v][1];
}
}
贿赂FIPA
FIPA(国际国际计划协会联合会)近期将进行投票,以确定下一届IPWC(国际规划世界杯)的主办方。钻石大陆的代表本内特希望通过以赠送钻石买通国家的方式,获得更多的投票。当然,他并不需要买通所有的国家,因为小国家会跟随着他们附庸的大国进行投票。换句话说,只要买通了一个大国,就等于获得了它和它统治下所有小国的投票。
例如,C在B的统治下,B在A的统治下,那么买通A就等于获得了三国的投票。
请注意,一个国家最多附庸于一个国家的统治下,附庸关系也不会构成环。
请你编写一个程序,帮助本内特求出在至少获得m个国家支持的情况下的最少花费是多少。
输入格式
输入包含多组测试数据。
第一行包含两个整数n和m,其中n表示参与投票的
国家的总数,m表示获得的票数。
接下来n行,每行包含一个国家的信息,形式如下:
CountryName DiamondCount DCName DCName …
其中CountryName是一个长度不超过100的字符串,表示这个国家的字,DiamondCount是一个整数,表示买通该国家需要的钻石DCName是一个字符串,表示直接附庸于该国家的一个国家的名字。
一个国家可能没有任何附庸国家。
当读入一行为#时,表示输入终止。
输出格式
每组数据输出一个结果,每个结果占一行。
数据范围
1≤n≤200,
0≤m≤n
输入样例:
3 2
Aland 10
Boland 20 Aland
Coland 15
#
输出样例:
20
输出样例:
20

#include<bits/stdc++.h>
using namespace std;
#define maxn 205
bool bz[maxn];
int tot,n,m,val[maxn],f[maxn][maxn],siz[maxn];
deque<int>q[maxn];
map<string,int>co;
void dp(int u)
{
f[u][0]=0;
siz[u]=1;
for(int i=0;i<q[u].size();++i)
{
int v=q[u][i];
dp(v);
siz[u]+=siz[v];
for(int j=min(m,siz[u]);j>=0;--j)
for(int k=j;k>=0;--k)
f[u][j]=min(f[u][j],f[u][k]+f[v][j-k]);
}
if(u)
for(int j=0;j<=min(m,siz[u]);++j)
f[u][j]=min(f[u][j],val[u]);
}
int main()
{
string s;
stringstream ss;
while(getline(cin,s))
{
if(s[0]=='#') return 0;
co.clear();
memset(bz,0,sizeof(bz));
memset(f,0x3f,sizeof(f));
for(int i=0;i<=n;++i) q[i].clear();
ss.clear();
ss<<s;
ss>>n>>m;
tot=0;
for(int i=1;i<=n;++i)
{
getline(cin,s);
ss.clear();
ss<<s;
ss>>s;
int u=co[s]?co[s]:(co[s]=++tot);
ss>>val[u];
while(ss>>s)
{
int v=co[s]?co[s]:(co[s]=++tot);
q[u].push_back(v);
bz[v]=1;
}
}
for(int i=1;i<=tot;++i)
if(!bz[i]) q[0].push_back(i);
dp(0);
printf("%d\n",f[0][m]);
}
}
P3047 Nearby Cows
一棵树,点带权,相连两点距离为1,求每个点距离不超过k的范围内的点权和。
1<=n<=1e5,1<=k<=20,0<=c<=1000.
更新时:\(V[u][j]+=V[fa][j-1]-V[u][j-2]\),\(j\)用倒序,否则\(V[u][j]\)值改变会影响\(V[u][j+2]\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5,K=22;
int n,k,te,tail[N],val[N][K];
struct e_
{
int v,pre;
}e[N<<1];
inline void add(int u,int v)
{
e[++te]=(e_){v,tail[u]};
tail[u]=te;
}
void dfs1(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==fa) continue;
dfs1(v,u);
for(int j=1;j<=k;++j) val[u][j]+=val[v][j-1];
}
}
void dfs2(int u,int fa)
{
for(int i=tail[u];i;i=e[i].pre)
{
int v=e[i].v;
if(v==fa) continue;
for(int j=k;j>=2;--j) val[v][j]+=val[u][j-1]-val[v][j-2];
val[v][1]+=val[u][0];
dfs2(v,u);
}
}
int sum(int x)
{
int res=0;
for(int i=0;i<=k;++i) res+=val[x][i];
return res;
}
int main()
{
scanf("%d %d",&n,&k);
for(int i=1,u,v;i<n;++i) scanf("%d %d",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;++i) scanf("%d",&val[i][0]);
dfs1(1,0);//每个点向下第k层的距离
dfs2(1,0);//ANS
for(int i=1;i<=n;++i) printf("%d\n",sum(i));
}
基环树DP
P6417 Mafija
题目描述
有 n个人,其中有一些人是平民,有一些人是坏蛋。
现在,平民们想揪出所有的坏蛋,于是 n 个人都指认了一个人是坏蛋。
如果一个人是平民,他会随便乱指认,否则,他会指认一个平民。
求出最多的坏蛋个数。
输入格式
第一行一个整数 n。
接下来 n 行,每行一个整数 k,第 i 行表示第 i个人指认了第 k个人。
输出格式
仅一行一个整数,表示最多的坏蛋个数。
输入输出样例
输入 #1复制
3
2
1
1
输出 #1复制
2
输入 #2复制
3
2
3
1
输出 #2复制
1
输入 #3复制
7
3
3
4
5
6
4
4
输出 #3复制
4
说明/提示
样例解释
样例输入输出 1 解释
坏蛋可以是第 2个人和第 3个人。
样例输入输出 2 解释
坏蛋可能是所有人,但是只能是其中的一个人,因为再多一个坏蛋的话会有坏蛋指控坏蛋的情况发生。
数据范围与限制
- 对于 40 分的数据,保证 n≤15。
- 对于 80 分的数据,保证 n≤2×104。
- 对于 100% 的数据,保证 1≤n≤5×105,1≤k≤n
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e5+5;
int n,f[N];
ll ans,dp[N][2],dp2[N][2];
bool vis[N];
vector<int>vv[N],H,Q;
int find(int x)
{
return f[x]!=x?f[x]=find(f[x]):x;
}
bool dfs(int u)
{
vis[u]=1;
for(int i=0;i<vv[u].size();++i)
{
int v=vv[u][i];
if(vis[v]||dfs(v)){H.push_back(u);return 1;}
}
return 0;
}
void dfs_(int u)
{
dp[u][1]=1;
vis[u]=1;
for(int i=0;i<vv[u].size();++i)
{
int v=vv[u][i];
if(vis[v]) continue;
dfs_(v);
dp[u][1]+=dp[v][0];
dp[u][0]+=max(dp[v][0],dp[v][1]);
}
}
int S;
ll calc(int x)
{
dp2[2][0]=dp[H[x]][1]+dp[H[x+1]][0];
dp2[2][1]=-1;
for(int j=3;j<=S;++j)
dp2[j][0]=max(dp2[j-1][0],dp2[j-1][1])+dp[H[x+j-1]][0],
dp2[j][1]=dp2[j-1][0]+dp[H[x+j-1]][1];
return dp2[S][0];
}
ll work()
{
memset(vis,0,sizeof(vis));
S=H.size()-1;
for(int i=1;i<=S;++i) vis[H[i]]=1;
for(int i=1;i<=S;++i) dfs_(H[i]),H.push_back(H[i]);
ll V=0;
for(int i=1;i<=S;++i) V=max(V,calc(i));
return V;
}
int main()
{
freopen("mafija.in","r",stdin);
freopen("mafija.out","w",stdout);
scanf("%d",&n);
for(int i=1,u;i<=n;++i) f[i]=i;
for(int i=1,u;i<=n;++i)
{
scanf("%d",&u);
vv[u].push_back(i);
int x=find(i),y=find(u);
if(x==y) Q.push_back(i);
else f[x]=y;
}
for(int i=0;i<Q.size();++i)
{
H.clear();
H.push_back(Q[i]);
dfs(Q[i]);
ans+=work();
}
printf("%lld",ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号